A wheel rolling along a rough horizontal surface with an angular velocity ω strikes a rough vertical wall, normally. Find the initial angular velocity, as it tends to roll up the wall (neglect any slippage) due to impulse.
Figure shows the two situation of a rolling wheel before and after its striking the wall.
If C2 is the point on the wall where the wheel strikes, then the impulseive force F passes through it. Moreover, the weight of the wheel mg and the normal reaction offered by the horizontal surface on the wheel to balance each other. So, the angular momentum of the wheel remains conserved about point C2.
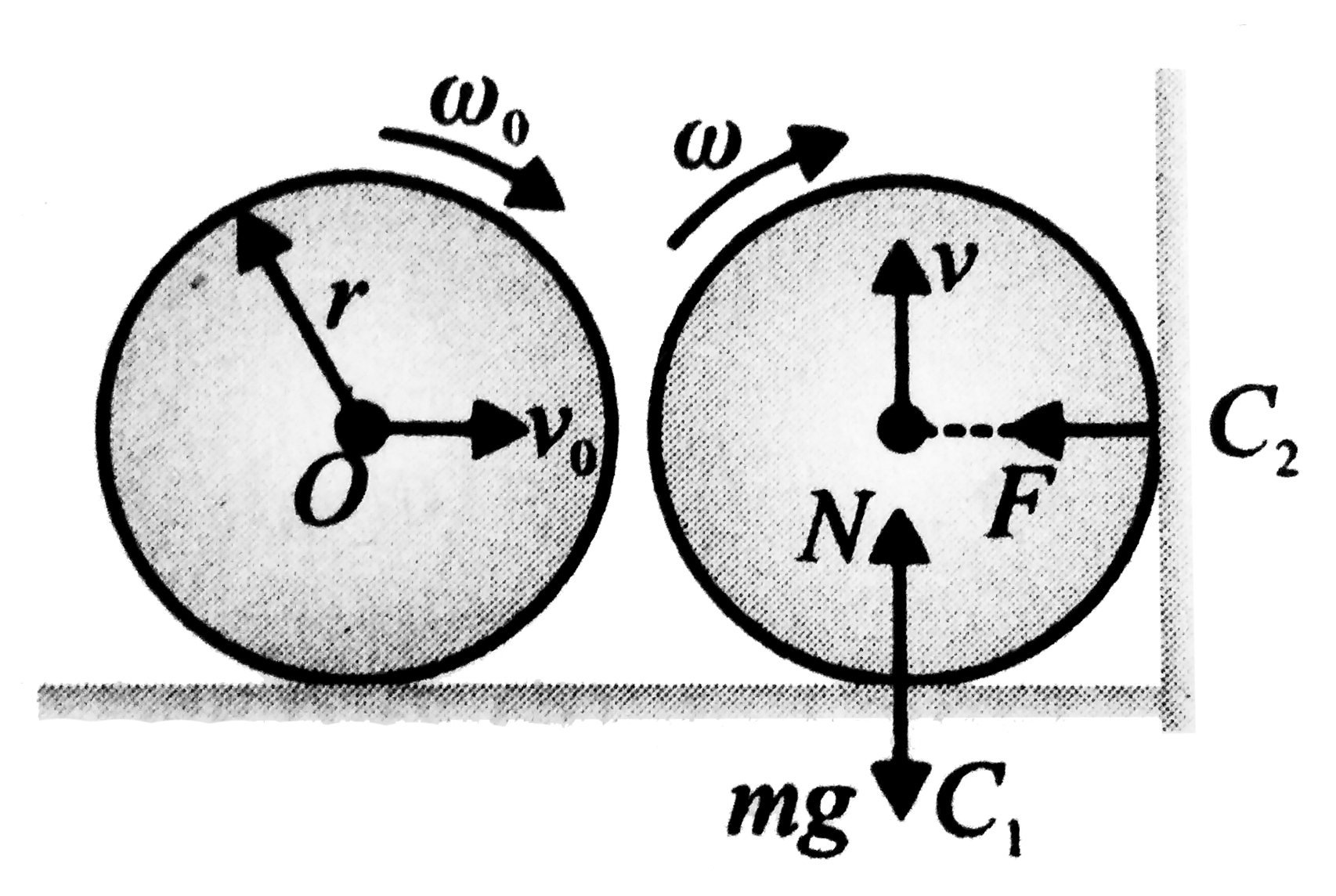
∴ Initial agular mometum = final agular momentum
∴Iω0=Iω+mvr
[where ω and v are the angular and linear speeds of the wheel, just after its striking]
Since slipage is prevented so v=ωr
∴Iω0=Iω=mωr2
⇒mr2ω02=mr2ωr=mωr2
⇒ω=ω03
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective19videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Single Correct142videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.321videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A uniform solid sphere of radius R, rolling without sliding on a horizontal surface with an angular velocity ω0, meets a rough inclined plane of inclination θ=60∘. The sphere starts pure rolling up the plane with an angular velocity ω Find the value of ω.
 View Solution
View SolutionA solid sphere spinning about a horizontal axis with an angular velocity ω is placed on a horizontal surface. Subsequently it rolls without slipping with an angular velocity of :
View Solution
Knowledge Check
- Question 1 - Select One
A sphere is performing pure rolling on a rough horizontal surface with constant angular velocity. Frictional force acting on the sphere is zero.
Velocity of contact point is zero.AStatement-1 is True, Statement-2 is Ture , Statement -2 is a correct explanation for statement -1.BStatement-1 is True, Statement-2 is True , Statement-2 is NOT a correct explanation fro Statement -1.CStatement-1 is True, Statement-2 is False.DStatement-1 is False, Statement-2 is True. - Question 2 - Select One
A sphere of radius R is rolling on a rough horizontal surface. The magnitude of velocity of A with respect to ground will be
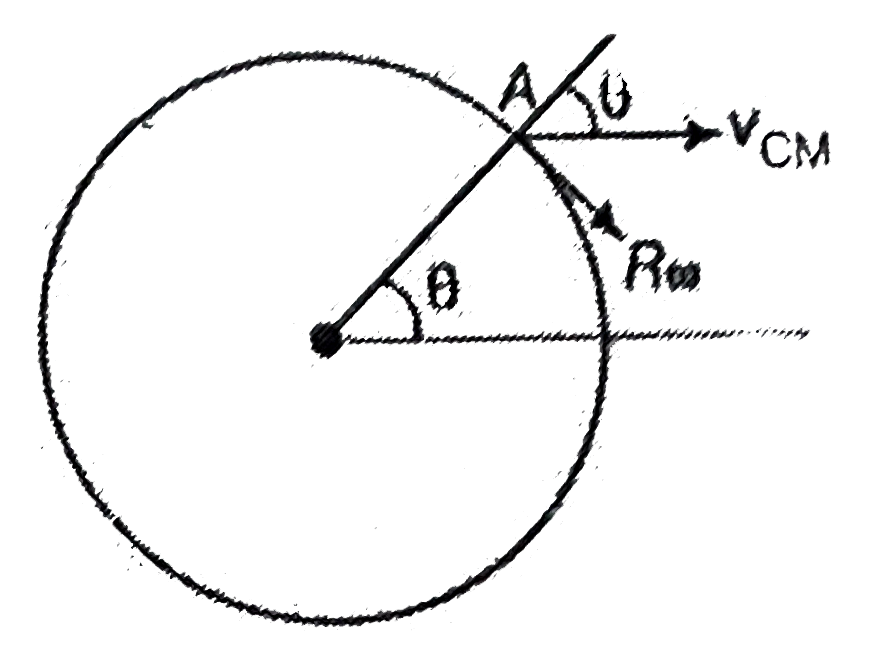 A√2vCMB2VCMsinθC√2vCM√1+sinθDNo sufficient information
A√2vCMB2VCMsinθC√2vCM√1+sinθDNo sufficient information - Question 3 - Select One
A sphere is moving on a smooth surface with linear speed v0 and angular velocity ω0. It finds a rough inclined surface and it starts climbing up:
 Aif v0>Rω0 friction force will act downwardsBif v0<Rω0, frictio force will act upwardsCif v0=Rω0 no friction force will actDif all above case friction will act upwards
Aif v0>Rω0 friction force will act downwardsBif v0<Rω0, frictio force will act upwardsCif v0=Rω0 no friction force will actDif all above case friction will act upwards
A sphere rolls on a horizontal surface. Is there any point of the sphere which has a vertical velocity?
View SolutionA solid sphere rolling on a rough horizontal surface with a linear speed v collides elastically with a fixed, smooth, vertical wall. Find the speed of the sphere after it has started pure rolling in the backward direction.
View Solution
The assembly of two discs as shown in figure is placed on a rough horizontal surface and the front disc is given an initial angular velocity ω0. Determine the final linear and angular velocity when both the discs start rolling. it is given that friction is sufficient to sustain rolling the rear wheel from the starting of motion.View SolutionA disc of radius R is moving on a rough horizontal surface with velocity v and angular speed ω at an instant as shown in figure. Choose the correct statement.
 View Solution
View Solution
A disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity the angle between the velocity ad acceleration vectors of point P isView Solution

