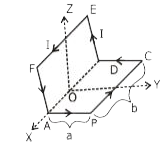
A wire carrying current I is bent in the shape ABCDEFA as shown, where rectangle ABCDA and ADEFA are perpendicular to each other. If the sides of the rectangles are of lengths a and b, then the magnitude and direction of magnetic moment of the loop ABCDEFA is:
√2 abl,along (ˆj√5+2ˆk√5)
abl,along (ˆj√5+2ˆk√5)
√2 abl,along (ˆj√2+ˆk√2)
abl, along (ˆj√2+√k√2)
The correct Answer is:C
LOOP = ABCD
→M1=(abI)(ˆj+ˆk)
Loop DEFA
→M2=(abI)ˆj
→M=→M1+→M2=abI(ˆj+ˆk)
∣∣→M∣∣=√2 abI
direction = along (ˆj√2+ˆk√2)
Topper's Solved these Questions
Similar Questions
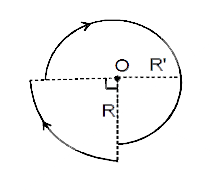
A current of I ampere is flowing through each of the bent wires as shown the magnitude and direction of magnetic field at O is
View SolutionA copper wire of length 7 metre is bent to form a circular loop. If i current flows through the loop, find out the magnitude of magnetic moment of the loop.
View Solution
Knowledge Check
A long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is
 Aμ0I4πR√1+π2Bμ0I4πR√2+π2Cμ0I4πR√4+π2Dμ0I4πR√9+π2
Aμ0I4πR√1+π2Bμ0I4πR√2+π2Cμ0I4πR√4+π2Dμ0I4πR√9+π2
A conducting wire carrying a current I is bent into the shape as shown. The net magnetic field at the centre O of the circular arc of radius RAμ0l2R(1+3ππ)Bμ0l4R(1+3ππ)Cμ0l8R(1+3ππ)Dμ0l8R(2+3ππ)A current of I ampere is flowing throught each of the bent wires as shown the magnitued and the bent wires as shown the magnitude the diection of magnetic field ot O is
 .A(μ0i4)(1R+2R')B(μ0i4)(1R+3R')C(μ0i8)(1R+32R')D(μ0i8)(1R+3R')
.A(μ0i4)(1R+2R')B(μ0i4)(1R+3R')C(μ0i8)(1R+32R')D(μ0i8)(1R+3R')
A square loop of side l carries a current i. it is placed as shown in figure. Find the magnetic moment of the loop.
View SolutionA loop of wire having 50 turns carries a current of 10A in anticlockwise direction. If diameter of loop is 10cm, what is the magnitude and direction of magnetic moment of current loop?
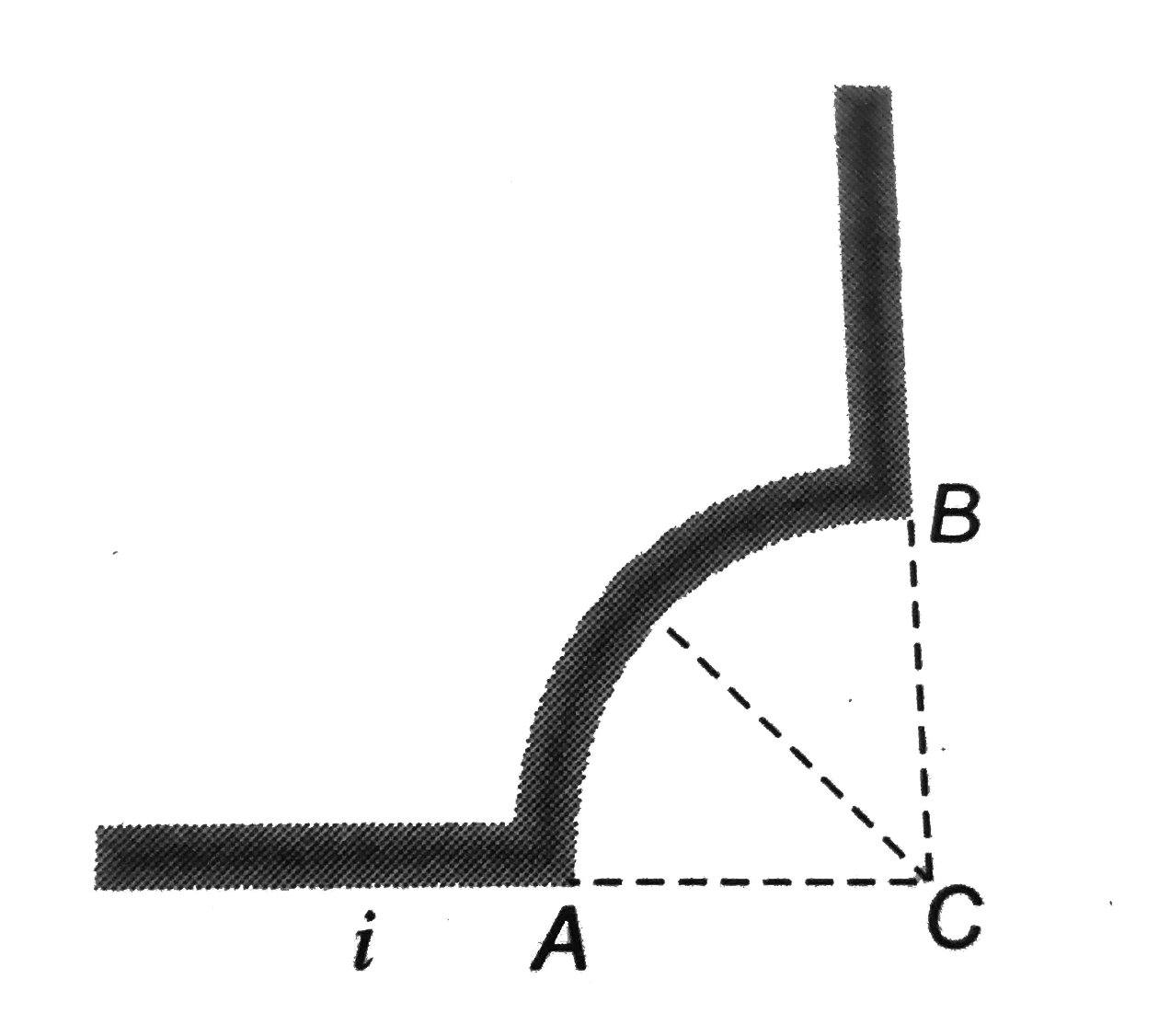
View SolutionA wire carrying current i is shaped as shown. Section AB is a quarter circle of radius r. The magnetic field is directed
View SolutionA wire of length 2 m carrying a current of 1 A is bent to form a circle, the magnetic moment of the coil is
View SolutionA wire of length 2 m carrying a current of 1 A is bent to form a circle, the magnetic moment of the coil is
View Solution
