A wire in the form of a circular loop of radius 10cm lies in a plane normal to a magnetic field of 100T. If this wire is pulled to take a square shape in the same plane in 0.1s, find the average induced emf in the loop.
To solve the problem, we need to find the average induced electromotive force (emf) when a circular loop of wire is transformed into a square loop while it is subjected to a magnetic field. Here’s a step-by-step breakdown of the solution:
Step 1: Calculate the initial area of the circular loop
The area A of a circular loop is given by the formula:
A=πR2
Where R is the radius of the circular loop. Given that R=10cm=0.1m:
Ainitial=π(0.1)2=π(0.01)=0.0314m2
Step 2: Determine the length of the wire
The circumference of the circular loop, which is the length of the wire, is given by:
L=2πR
Substituting the value of R:
L=2π(0.1)=0.2πm≈0.6283m
Step 3: Calculate the side length of the square loop
Since the wire is reshaped into a square, the perimeter of the square is equal to the length of the wire:
Perimeter of square=4s=L⟹s=L4
Where s is the side length of the square:
s=0.2π4=π20m≈0.1571m
Step 4: Calculate the area of the square loop
The area A of the square loop is given by:
Afinal=s2=(π20)2=π2400≈0.0247m2
Step 5: Determine the change in area
The change in area ΔA as the loop transforms from circular to square is:
ΔA=Afinal−Ainitial=0.0247−0.0314=−0.0067m2
Step 6: Calculate the average induced emf
The average induced emf E can be calculated using Faraday's law of electromagnetic induction:
E=−ΔΦΔt
Where ΔΦ=BΔA and B=100T (the magnetic field strength) and Δt=0.1s:
ΔΦ=BΔA=100×(−0.0067)=−0.67Wb
Thus, the average induced emf is:
E=−−0.670.1=6.7V
Final Answer:
The average induced emf in the loop is E=6.7V.
The area A of a circular loop is given by the formula:
A=πR2
Where R is the radius of the circular loop. Given that R=10cm=0.1m:
Ainitial=π(0.1)2=π(0.01)=0.0314m2
The circumference of the circular loop, which is the length of the wire, is given by:
L=2πR
Substituting the value of R:
L=2π(0.1)=0.2πm≈0.6283m
Since the wire is reshaped into a square, the perimeter of the square is equal to the length of the wire:
Perimeter of square=4s=L⟹s=L4
Where s is the side length of the square:
s=0.2π4=π20m≈0.1571m
The area A of the square loop is given by:
Afinal=s2=(π20)2=π2400≈0.0247m2
The change in area ΔA as the loop transforms from circular to square is:
ΔA=Afinal−Ainitial=0.0247−0.0314=−0.0067m2
The average induced emf E can be calculated using Faraday's law of electromagnetic induction:
E=−ΔΦΔt
Where ΔΦ=BΔA and B=100T (the magnetic field strength) and Δt=0.1s:
ΔΦ=BΔA=100×(−0.0067)=−0.67Wb
Thus, the average induced emf is:
E=−−0.670.1=6.7V
The average induced emf in the loop is E=6.7V.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise 27.2
4 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise 27.3
4 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Miscellaneous Examples
5 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
A wire of length l in the form of a square loop lies in a plane normal to a magnetic field B0. If this wire is converted into a circular loop in time, then find the average induced emf.
View SolutionA conducintg circular loop having a redius of 5.0cm, is placed perpendicular to a magnetic field of 0.50 T. It is removed from the field in 0.50 s. Find the average emf produced In the loop during this time.
View SolutionA semi-circular loop of radius R is placed in a uniform magnetic field as shown. It is pulled with a constant velocity. The induced emf in the loop is
View SolutionA circular loop of radius R=20 cm is placed in a uniform magnetic field B=2T in xy-plane as shown in figure. The loop carries a current i=1.0A in the direction shown in figure. Find the magnitude of torque acting on the loop.
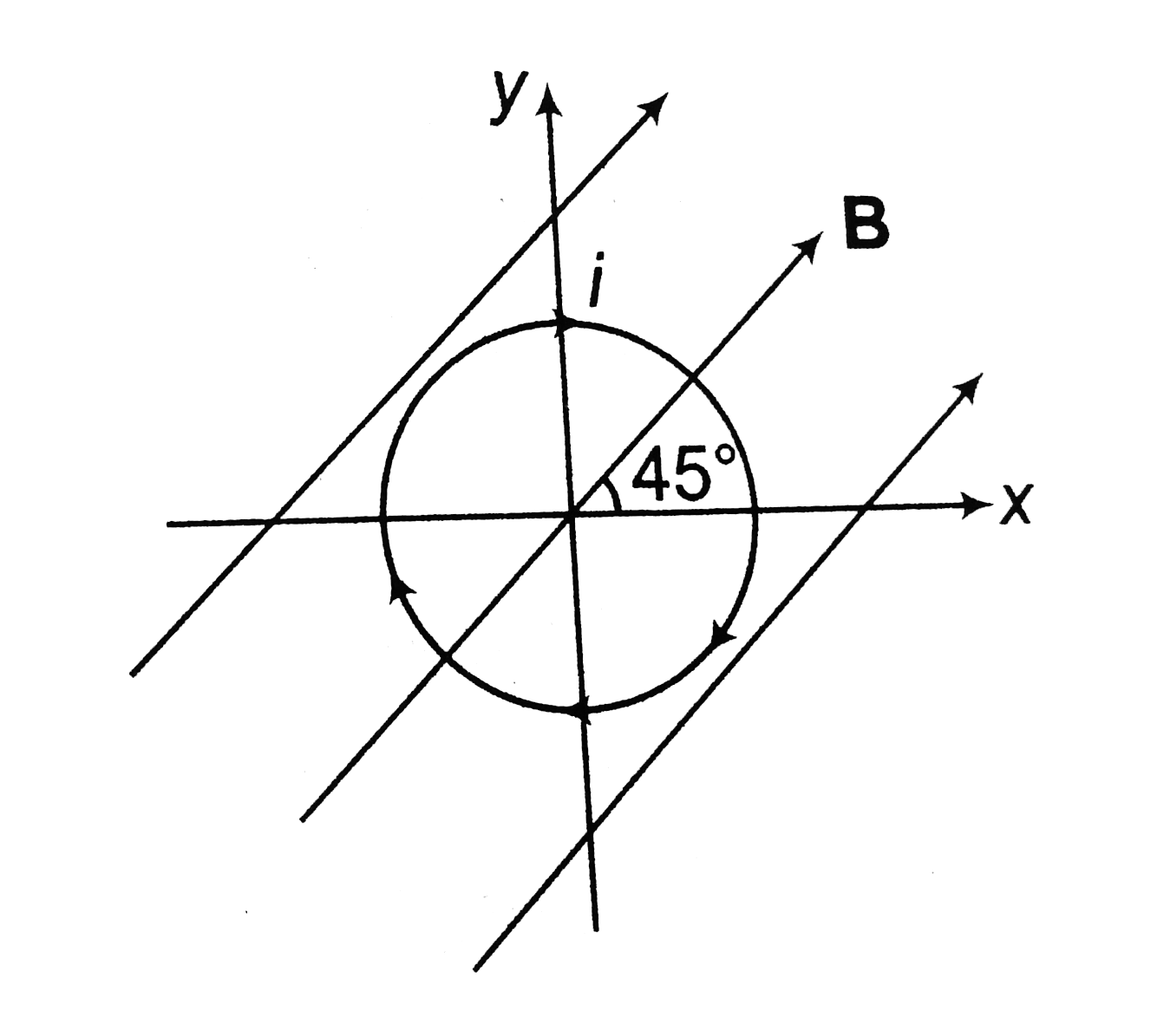
View SolutionA circular loop of radius R=20 cm is placed in a uniform magnetic field B=2T in xy-plane as shown in figure. The loop carries a current i=1.0A in the direction shown in figure. Find the magnitude of torque acting on the loop.

View SolutionA given wire is bent into a rectangular loop of size 15cm×5cm and placed perpendicular to a magnetic field of 1.0 Tesla. Within 0.5sec, the loop is changed into a 10cm square and the field increases to 1.4 Tesla.Calculate the value of e.m.f. induced in the loop?
View SolutionA uniform magnetic field B=0.5T exists in a circular region of radius R=5m. A loop of radius R=5m encloses the magnetic field at t=0 and then pulled at uniform speed v=2ms−1 In the plane of the paper. Find the induced emf (inV) in the loop at time t=3s.

View SolutionA long wire having a semi-circular loop of radius r carries a current I, as shown in Fig. Find the magnetic field due to entire wire.

View SolutionA circular loop of radius R is kept in a uniform magnetic field pointing perpendicular into the plane of paper. When a current l flows in the loop, the tension produced in the loop is
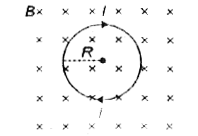
View SolutionA conducting circular loop is placed is a uniform magnetic field B =0.20 T with its plane perpendicular to the field . Somehow, the radius of the loop starts shrinking at a constant rate of 1.0mms−1. Find the induced emf in the loop at an instant when the radius is 2 cm.
View Solution
