
A wire is bent an an angle . A rod of mass m can slide along the bended wire without friction as shown in Fig. A soap film is maintained in the frame kept in a vertical position and the rod is in equilibrium as shown in the figure. If rod is displaced slightly in vertical direction, then the time period of small oscillation of the rod is
The correct Answer is:A
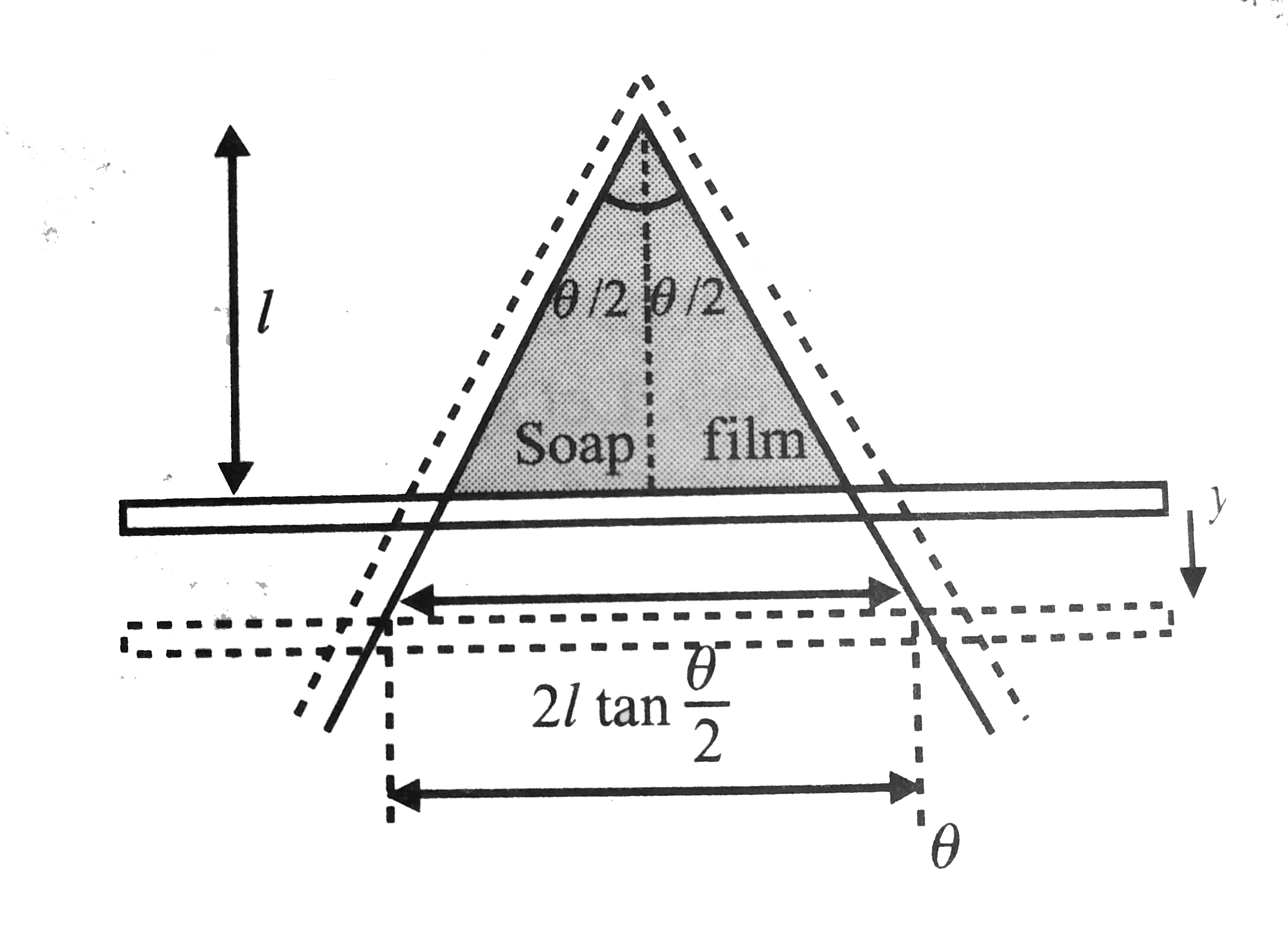
Let S be the surface tension of the soap film. For equilibrium of rod
,
If the rod is displaced from its mean position by small displacement y, then restoring fornce on the rod is
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning
6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective
21 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
A rod of mass m can move vertically on two fixed inclined rod in vertical plane, weight of the rod is blanced by thin liquid film between rods as shown. (Surface tension of liquid is S).
If rod is displaced a little in downward direction and released, then what will be the time period of oscillation of rod.

View SolutionA uniform rod ofmass M and length L is hanging from its one end free to rotate in a veritcal plane.A small ball of equal mass is attached of the lowe end as shown. Time period of small oscillations of the rod is
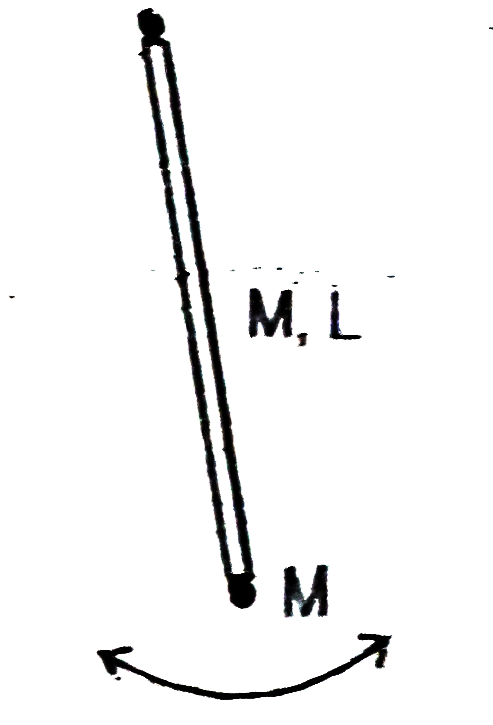
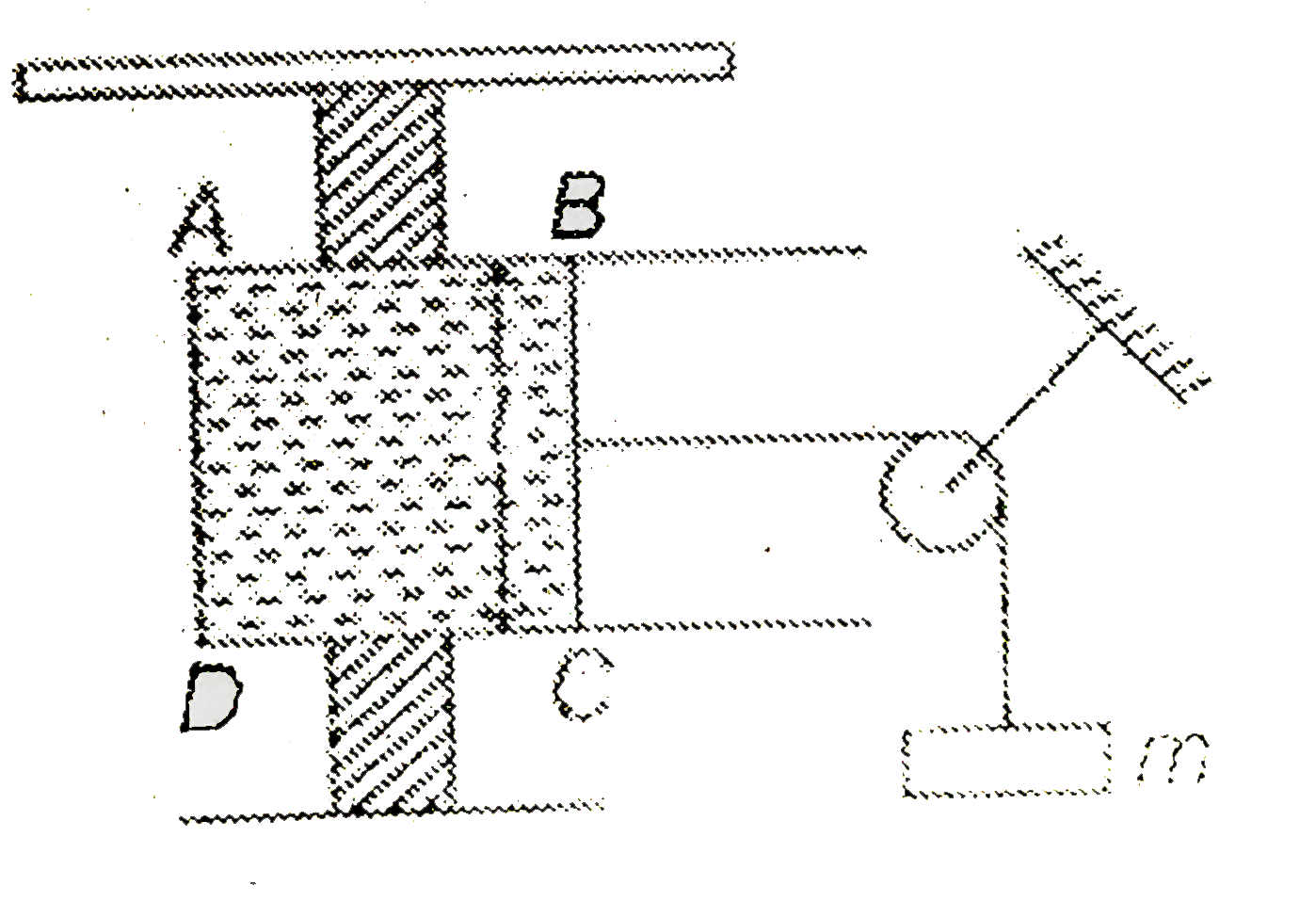
View SolutionA wire frame ABCD has a soap film. The wire BC can slide on the frame without friction and it is in equilibrium in the position shown in the figure. Find m, if T is the surface tension of the liquid.
View SolutionA rod of mass m and length L is kept on a horizontal smooth surface. The rod is hinged at its one end A. There are two springs, perpendicular to the rod, kept in the same horizontal plane. The spring of spring constant k is rigidly attached to the lower end of rod and spring of spring constant 12k just touches the rod at its midpoint C, as shown in the figure. If the rod is slightly displaced leftward and released then, the time period for small osciallation of the rod will be

View SolutionA system of two identical rods (L-shaped) of mass m and length l are resting on a peg P as shown in the figure. If the system is displaced in its plane by a small angle θ,find the period of oscillations:

View SolutionA uniform rod ofmass M and length L is hanging from its one end free to rotate in a veritcal plane.A small ball of equal mass is attached of the lowe end as shown. Time period of small oscillations of the rod is
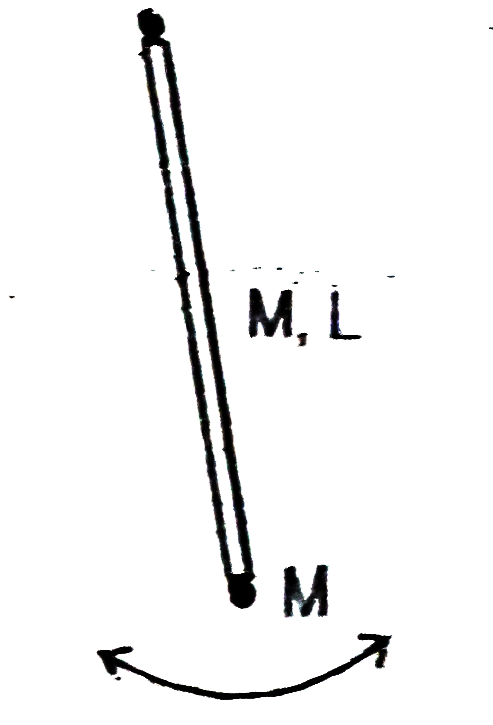
View SolutionA uniform nonconducting rod of mass ma and length l, with charge density λ as shown in fig. is hanged at the midpoint at origin so that it can rotate in a horizontal plane without any friction. A uniform electric field E exists parallel to x axis in the entire region. Calculated the period of small oscillation of the rod .

View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What is the rate of change of angular momentum of the rod ?
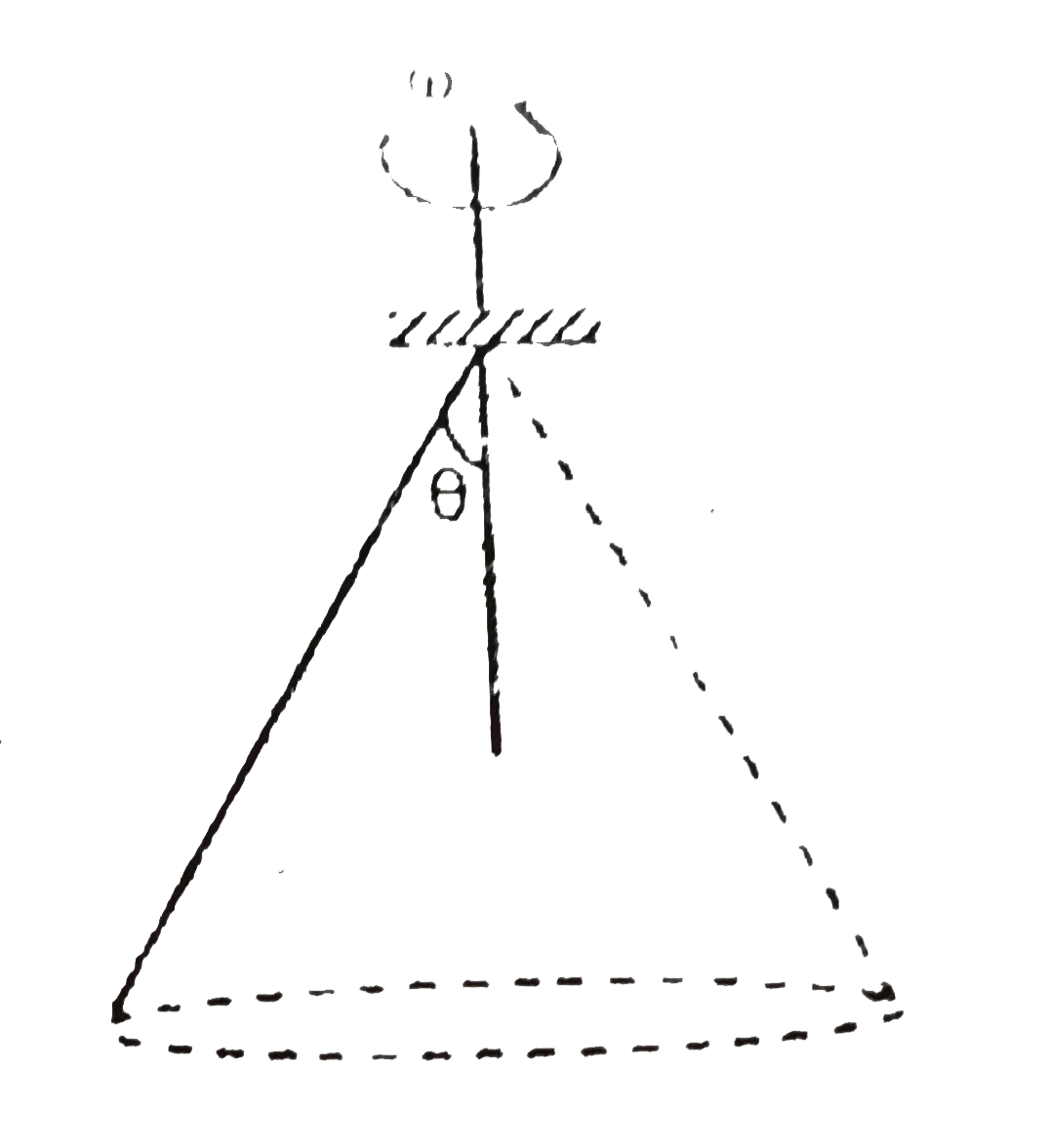
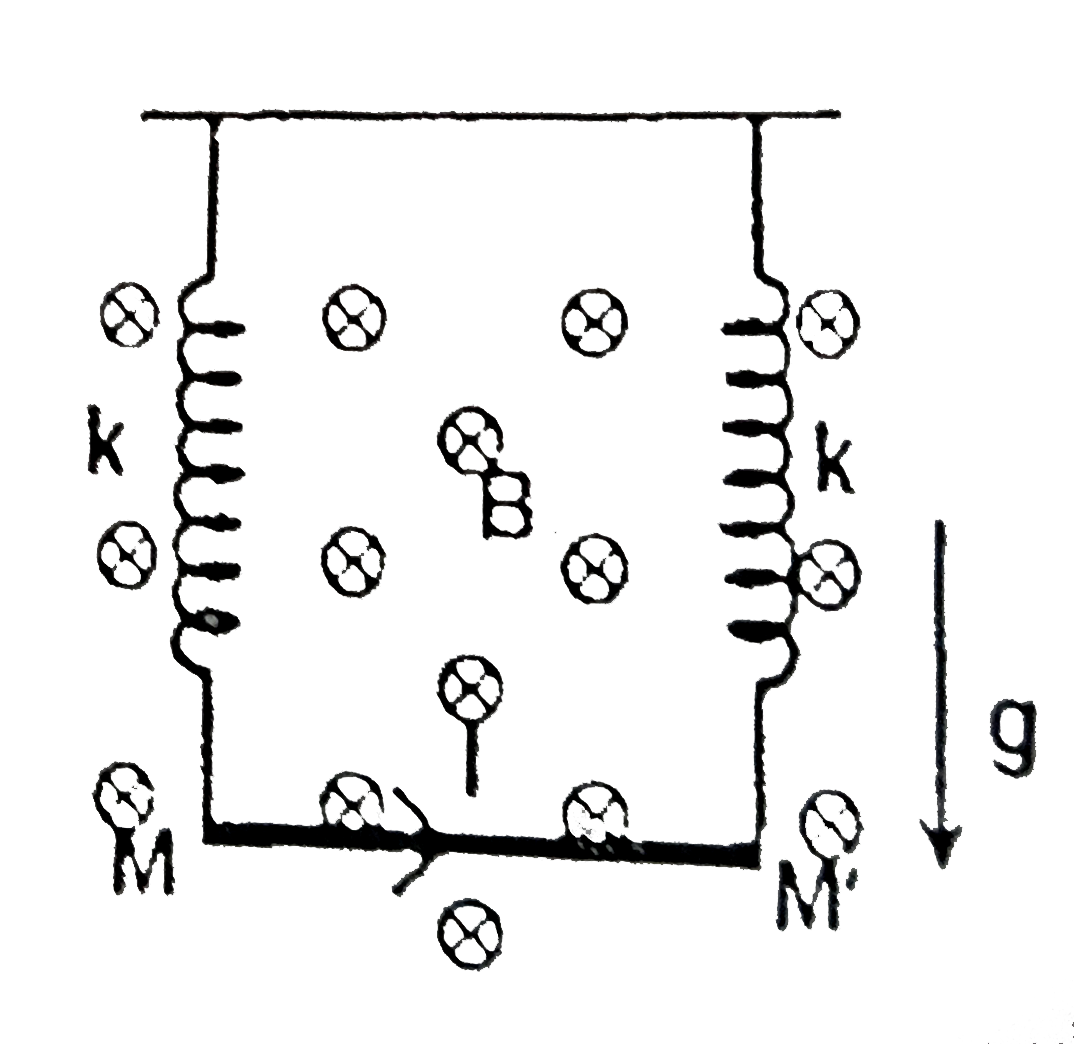
View SolutionConsider the plane of the paper to be vertical plane with direction of 'g' as shown in the figure. A rod (MM') of mass 'M' and carrying a current I. The rod is suspended vertically through two insulated spring of spring constant K at two ends. A uniform magnetic field is applied perpendicular to the plane of the paper such that the potential energy stored in the spring, in equilibrium position is zero. If the rod is slightly displaced in the vertically direction from the position of equilibrium, then the time period of oscillation is
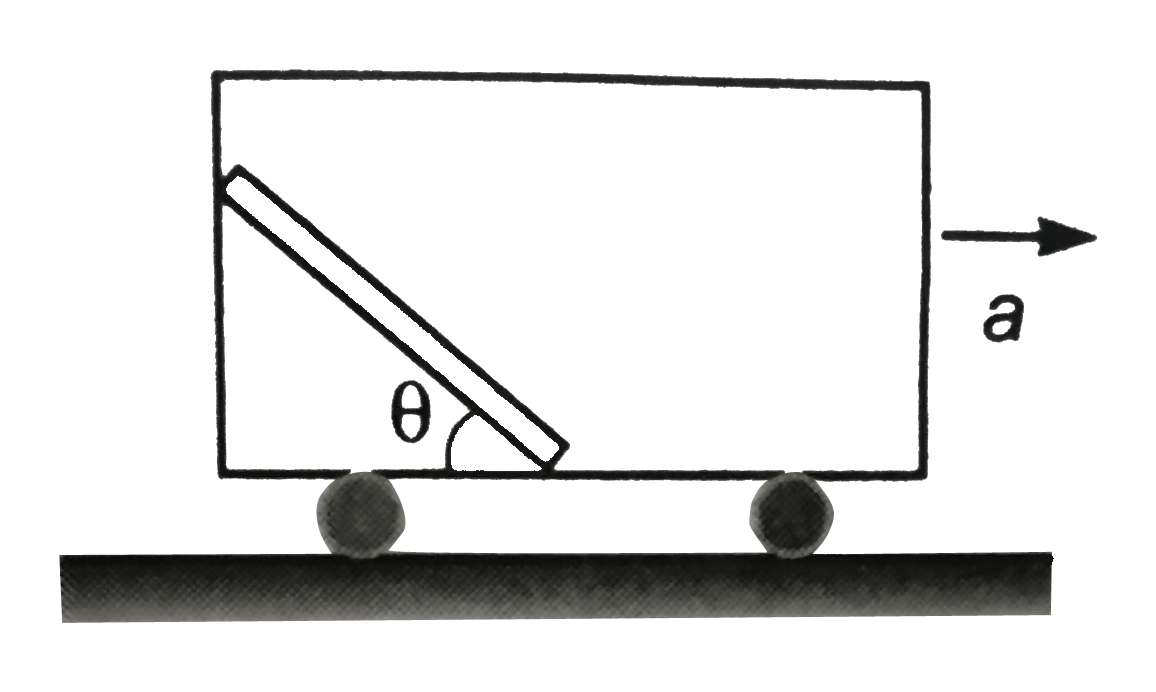
View SolutionA smooth rod length l is kept inside a trolley at an angle θ as shown in the figure. What should be the acceleration a of the trolley so that the rod remain in equilibrium with respect to it?
View Solution
