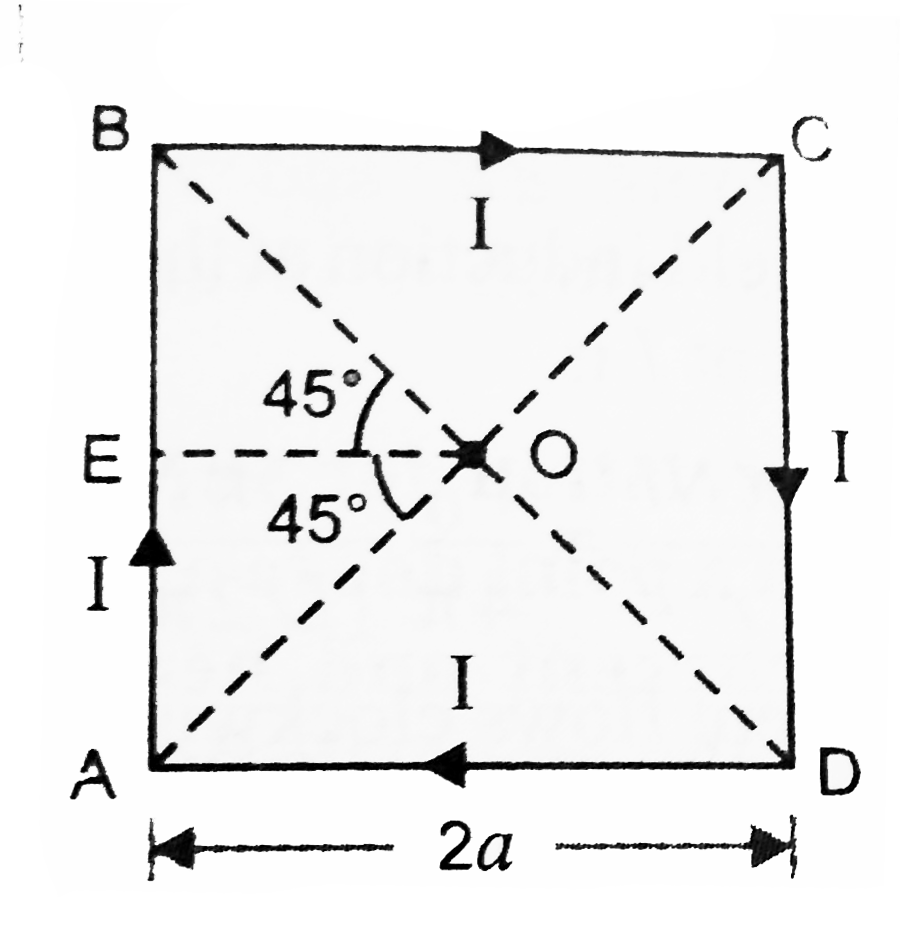
A wire of length l is bent in the form of an equilateral triangle and carries an electric current i. (a) Find the magnetic field B at the centre. (b) If the wire is bent in the form of a square, what would be the value of B at the centre?
To solve the problem step by step, we will find the magnetic field at the center of a wire bent in the shape of an equilateral triangle and then for a square.
Part (a): Magnetic Field at the Center of an Equilateral Triangle
1. Identify the Geometry:
- The wire is bent into the shape of an equilateral triangle with a total length L. Each side of the triangle will have a length of L3.
2. Determine the Center:
- The center of the equilateral triangle is the point where the three medians intersect. This point is equidistant from all three vertices.
3. Calculate the Distance from Center to Side:
- The distance from the center (O) to any side (let's say AB) can be calculated using trigonometry. The height of the triangle can be found as:
Height=√32⋅L3
- The distance from the center to the side (OP) is:
OP=13⋅Height=13⋅√32⋅L3=L6√3
4. Calculate the Magnetic Field due to One Side:
- The magnetic field B due to a straight current-carrying wire at a distance d is given by:
B=μ0I4πd
- For one side of the triangle, substituting d=L6√3:
BAB=μ0I4π⋅L6√3=6√3μ0I4πL
5. Total Magnetic Field at the Center:
- Since the triangle is symmetrical, the magnetic fields due to each side will have the same magnitude. The total magnetic field at the center will be the vector sum of the fields from all three sides. Each of these fields contributes equally and adds up:
Btotal=3⋅BAB=3⋅6√3μ0I4πL=18√3μ0I4πL=9√3μ0I2πL
Part (b): Magnetic Field at the Center of a Square
1. Identify the Geometry:
- The wire is now bent into the shape of a square with a total length L. Each side of the square will have a length of L4.
2. Determine the Center:
- The center of the square is the point where the diagonals intersect.
3. Calculate the Distance from Center to Side:
- The distance from the center to any side (let’s say AB) is half the length of the side:
OP=L8
4. Calculate the Magnetic Field due to One Side:
- Using the same formula for the magnetic field:
BAB=μ0I4π⋅L8=2μ0IπL
5. Total Magnetic Field at the Center:
- Since the square is symmetrical, the magnetic fields due to each side will have the same magnitude and direction towards the center:
Btotal=4⋅BAB=4⋅2μ0IπL=8μ0IπL
Final Answers:
- (a) The magnetic field at the center of the equilateral triangle is 9√3μ0I2πL.
- (b) The magnetic field at the center of the square is 8μ0IπL.
- The wire is bent into the shape of an equilateral triangle with a total length L. Each side of the triangle will have a length of L3.
- The center of the equilateral triangle is the point where the three medians intersect. This point is equidistant from all three vertices.
- The distance from the center (O) to any side (let's say AB) can be calculated using trigonometry. The height of the triangle can be found as:
Height=√32⋅L3
- The distance from the center to the side (OP) is:
OP=13⋅Height=13⋅√32⋅L3=L6√3
- The magnetic field B due to a straight current-carrying wire at a distance d is given by:
B=μ0I4πd
- For one side of the triangle, substituting d=L6√3:
BAB=μ0I4π⋅L6√3=6√3μ0I4πL
- Since the triangle is symmetrical, the magnetic fields due to each side will have the same magnitude. The total magnetic field at the center will be the vector sum of the fields from all three sides. Each of these fields contributes equally and adds up:
Btotal=3⋅BAB=3⋅6√3μ0I4πL=18√3μ0I4πL=9√3μ0I2πL
- The wire is now bent into the shape of a square with a total length L. Each side of the square will have a length of L4.
- The center of the square is the point where the diagonals intersect.
- The distance from the center to any side (let’s say AB) is half the length of the side:
OP=L8
- Using the same formula for the magnetic field:
BAB=μ0I4π⋅L8=2μ0IπL
- Since the square is symmetrical, the magnetic fields due to each side will have the same magnitude and direction towards the center:
Btotal=4⋅BAB=4⋅2μ0IπL=8μ0IπL
- (a) The magnetic field at the center of the equilateral triangle is 9√3μ0I2πL.
- (b) The magnetic field at the center of the square is 8μ0IπL.
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 27videos
MAGNETIC FIELD DUE TO CURRENT
- BOOK - HC VERMACHAPTER - MAGNETIC FIELDEXERCISE - Exercises61videos
MAGNETIC FIELD
- BOOK - HC VERMACHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Exercises9videos
MAGNETIC PROPERTIES OF MATTER
Similar Questions
Knowledge Check
- Question 1 - Select One
A conducting wire of length L is bent in the form of an equilateral triangle. If current I is made to pass through it, then calculate the magnetic field intensity at the centre of the triangle.
A27μ0I4πLB27μ0I2πLC27μ0I5πLD27μ0I7πL - Question 2 - Select One
Magnetic field at the centre of coil of n turns, bent in the form of a square of side 2l, carrying current i, is
A0.5×10−5TB1.25×10−4TC3.0×10−5TD4×10−5T - Question 3 - Select One
The wire of length L is bent in the form of square and circle.The ratio of their magnetic moment at their centre is
Aπ/4Bπ/6Cπ/2Dπ
A uniform wire of length L is bent in the form of a circle.The shift in its centre of mass is
View SolutionFind an expression for the magnetic field induction at the centre of a coil bent in the form of a square of side 2a, carrying current I, figure
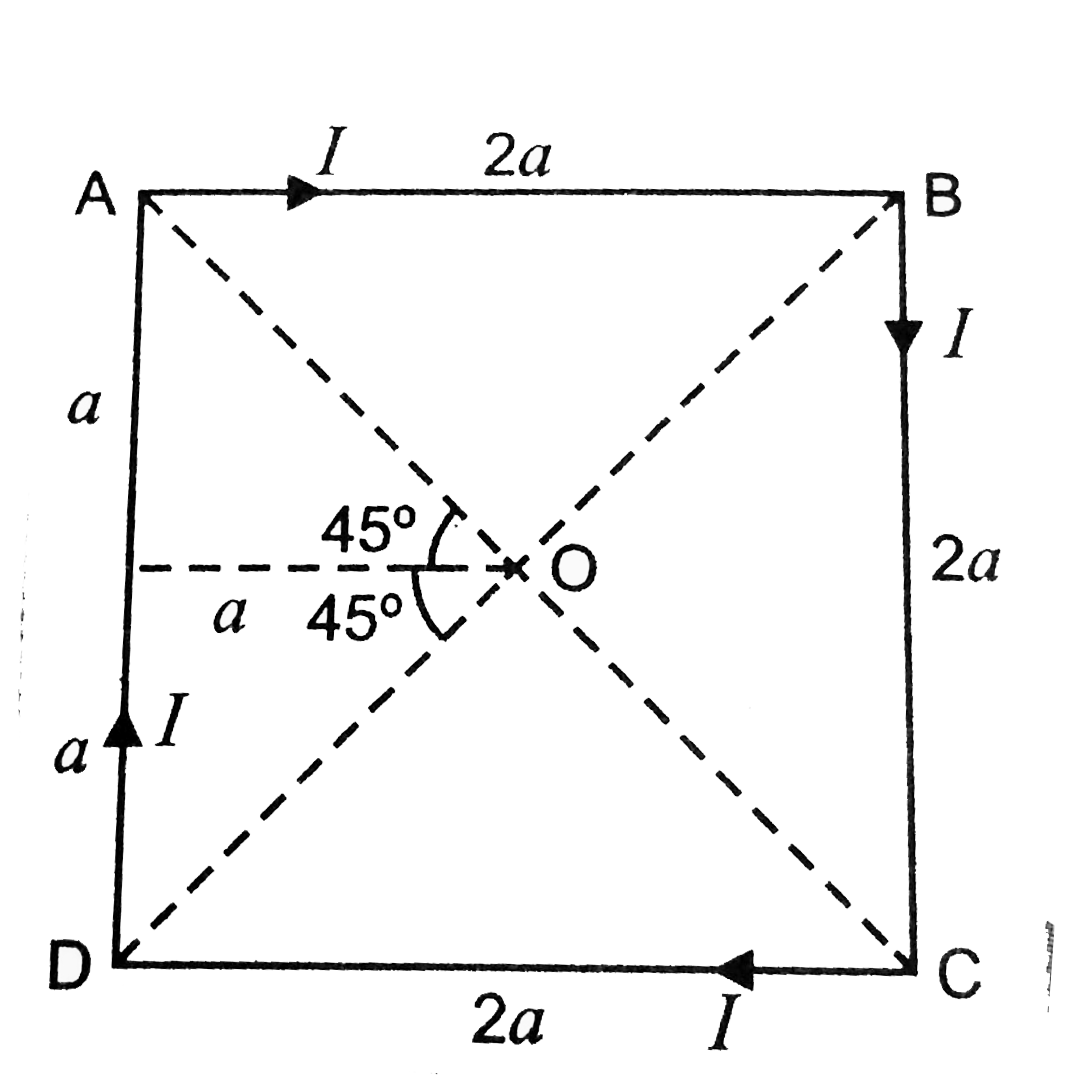 View Solution
View SolutionIf a thin uniform wire of length 1 m is bent into an equilateral triangle and carries a current of √3A in anitclockwise direction, find the net magnetic induction at the centroid
View SolutionA wire of length L carrying a current I is bent into a circle. The magnitude of the magnetic field at the centre of the circle is
View SolutionA copper wire is bent in the form of an equilateral triangle of area 4√3cm2 .If the same wire is bent into the form of a square, the area of the square will be :
View Solution