A wire of mass 5 gm is kept horizontally on the surface of water. What ist he minimum length of the wire so that it does not break the surface film.Surface tension =72×10−3N/m
To find the minimum length of the wire so that it does not break the surface film of water, we can follow these steps:
1. Understand the Forces Involved:
The wire experiences an upward force due to surface tension. The total upward force acting on the wire is given by the formula:
F=2×T×L
where T is the surface tension and L is the length of the wire.
2. Identify the Weight of the Wire:
The weight of the wire, which acts downward, can be calculated using the formula:
W=m×g
where m is the mass of the wire and g is the acceleration due to gravity (approximately 9.8m/s2).
3. Convert Mass to Kilograms:
The mass of the wire is given as 5g. Convert this to kilograms:
m=5g=5×10−3kg
4. Calculate the Weight of the Wire:
Substitute the mass into the weight formula:
W=5×10−3kg×9.8m/s2=4.9×10−2N
5. Set Up the Equation for Equilibrium:
For the wire to float without breaking the surface film, the upward force due to surface tension must equal the weight of the wire:
2×T×L=W
6. Substitute Values:
Substitute the known values into the equation:
2×(72×10−3N/m)×L=4.9×10−2N
7. Solve for Length L:
Rearranging the equation gives:
L=4.9×10−22×72×10−3
L=4.9×10−2144×10−3=4.9144≈0.3403m
8. Final Result:
The minimum length of the wire so that it does not break the surface film is approximately:
L≈0.34m
The wire experiences an upward force due to surface tension. The total upward force acting on the wire is given by the formula:
F=2×T×L
where T is the surface tension and L is the length of the wire.
The weight of the wire, which acts downward, can be calculated using the formula:
W=m×g
where m is the mass of the wire and g is the acceleration due to gravity (approximately 9.8m/s2).
The mass of the wire is given as 5g. Convert this to kilograms:
m=5g=5×10−3kg
Substitute the mass into the weight formula:
W=5×10−3kg×9.8m/s2=4.9×10−2N
For the wire to float without breaking the surface film, the upward force due to surface tension must equal the weight of the wire:
2×T×L=W
Substitute the known values into the equation:
2×(72×10−3N/m)×L=4.9×10−2N
Rearranging the equation gives:
L=4.9×10−22×72×10−3
L=4.9×10−2144×10−3=4.9144≈0.3403m
The minimum length of the wire so that it does not break the surface film is approximately:
L≈0.34m
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 3 (SOLVED EXAMPLES)
31 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 4 (SOLVED EXAMPLES)
11 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 4 ( TEMPERATURE ) UNSOLVED PROBLEMS
12 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)
2 Videos
- SAMPLE QUESTION PAPER - 01 BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER - 01 EXERCISE - SECTION - D
12 Videos
Similar Questions
A wire of mass 1g is kept horizontally on the surface of water. The length of the wire that does not break the surface film is (surface tension of water is 70dy≠cm−1)
View SolutionA metallic wire of diameter d is lying horizontally on the surface of water. The maximum length of wire so that it may not sink will be
View SolutionCalculate the pressue inside air bubble of diameter 0.2 mm situated just below the surface of water. Surface tension of water is 72×10−3Nm−1.
View SolutionA soap film is created in a small wire frame as shown in the figure. The sliding wire of mass m is given a velocity u to the right and assume that u is small enough so that film does not break. Plane of the film is horizontal and surface tension is T, then time to region the original position of wire is equal to :
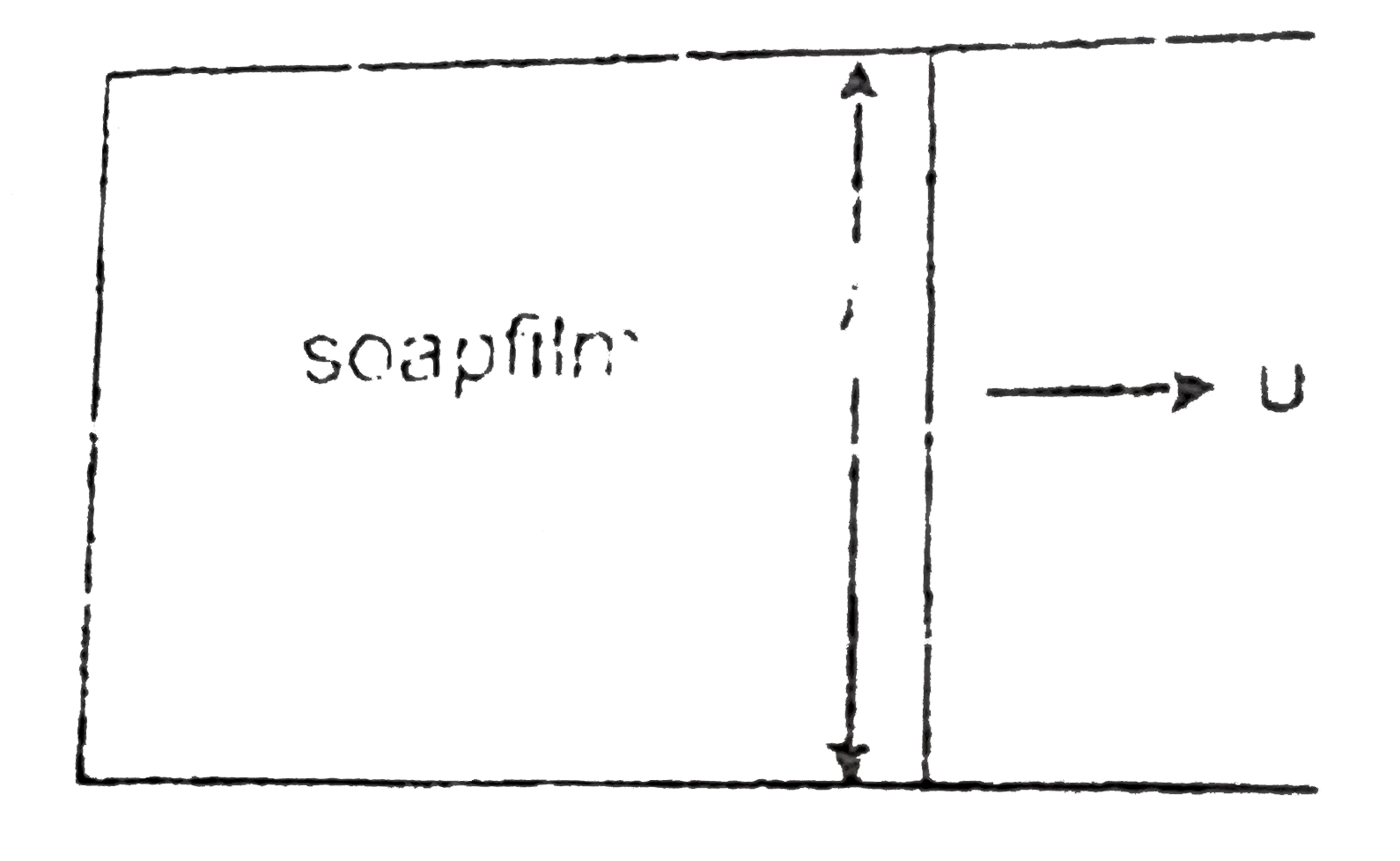
View SolutionA wire 0.1m long is placed horizontally on the surface of water and is gently pulled up with a force of 1.456×10−2N to keep the wire in equilibrium. Calculate the surface tension of water.
View SolutionA 10 cm long wire is placed horizontal on the surface of water and is gently pulled up with a force of 2×10−2 N to keep the wire in equilibrium. The surface tension, in Nm−1 of water is
View SolutionWhat should be the radius of a water drop so that the excess pressure inside it is 0.2 atm? Surface tension of water is 72×10−3N/m?
View SolutionTwo masses 7 kg and 12 kg are connected at the two ends of a metal wire that goes ove a frictionless puulley. What should be in the minimum radius of the wire in order that the wire does not break,if the breaking stess of the metal is 1.3×108N/m2 ?
View SolutionA rectangular glass plate of dimensions 5 cm × 4 cm is placed flat on the surface of water. Find the downward force on the plate due to surface tension. Given surface tension of water = 0.073 N m−1
View SolutionThe minimum force required to separate a light glass plate of perimeter 5m from a water surface is (Given surface tension of water = 70×10−3N/m)
View Solution
