A wire of mass 9.8×10−3 kg per meter passes over a frictionless pulley fixed on the top of an inclined friction less plane which makes an angle of 30∘ with the horizontal Masses M1 and M2 are tied at the two ends of the wire The mass M1 rests on the plane and mass M2 hangs freely vertically downwards . The whole system is in equilibrium Now a transverse wave propagates along the wire with a velocity of 100m/s If g=9.8m/s2 calculate the value of masses M1 and M2 .
To solve the problem, we need to analyze the forces acting on the two masses M1 and M2 and use the information about the wave velocity to find their values. Here’s a step-by-step breakdown:
Step 1: Analyze the Forces
1. For Mass M2 (hanging vertically):
- The force acting downward is the weight of M2: M2g.
- The tension T in the wire acts upward.
- In equilibrium, these forces are balanced:
M2g=T(Equation 1)
2. For Mass M1 (on the inclined plane):
- The weight of M1 can be resolved into two components:
- Perpendicular to the incline: M1gcos(30∘)
- Parallel to the incline: M1gsin(30∘)
- The tension T acts up the incline.
- In equilibrium, the forces along the incline are balanced:
T=M1gsin(30∘)(Equation 2)
Step 2: Relate the Two Equations
From Equation 1, we have:
T=M2g
From Equation 2, we have:
T=M1gsin(30∘)
Setting these equal gives:
M2g=M1gsin(30∘)
Dividing both sides by g (assuming g≠0):
M2=M1sin(30∘)
Since sin(30∘)=12, we can write:
M2=12M1(Equation 3)
Step 3: Use the Wave Velocity to Find Tension
The velocity of a transverse wave on a string is given by:
v=√Tμ
Where:
- v=100m/s (given)
- μ=9.8×10−3kg/m (mass per unit length of the wire)
Squaring both sides:
v2=Tμ
Rearranging gives:
T=μv2
Substituting the values:
T=(9.8×10−3)×(100)2
T=(9.8×10−3)×10000=98N
Step 4: Find Masses M1 and M2
Using Equation 1:
M2g=T
Substituting g=9.8m/s2:
M2⋅9.8=98
Solving for M2:
M2=989.8=10kg
Using Equation 3:
M2=12M1⟹10=12M1
Solving for M1:
M1=20kg
Final Answer
Thus, the values of the masses are:
- M1=20kg
- M2=10kg
1. For Mass M2 (hanging vertically):
- The force acting downward is the weight of M2: M2g.
- The tension T in the wire acts upward.
- In equilibrium, these forces are balanced:
M2g=T(Equation 1)
- The weight of M1 can be resolved into two components:
- Perpendicular to the incline: M1gcos(30∘)
- Parallel to the incline: M1gsin(30∘)
- The tension T acts up the incline.
- In equilibrium, the forces along the incline are balanced:
T=M1gsin(30∘)(Equation 2)
From Equation 1, we have:
T=M2g
From Equation 2, we have:
T=M1gsin(30∘)
Setting these equal gives:
M2g=M1gsin(30∘)
Dividing both sides by g (assuming g≠0):
M2=M1sin(30∘)
Since sin(30∘)=12, we can write:
M2=12M1(Equation 3)
The velocity of a transverse wave on a string is given by:
v=√Tμ
Where:
- v=100m/s (given)
- μ=9.8×10−3kg/m (mass per unit length of the wire)
v2=Tμ
Rearranging gives:
T=μv2
Substituting the values:
T=(9.8×10−3)×(100)2
T=(9.8×10−3)×10000=98N
Using Equation 1:
M2g=T
Substituting g=9.8m/s2:
M2⋅9.8=98
Solving for M2:
M2=989.8=10kg
M2=12M1⟹10=12M1
Solving for M1:
M1=20kg
Thus, the values of the masses are:
- M1=20kg
- M2=10kg
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISES40videos
LAWS OF MOTION
- BOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Additional Examples / Exercises6videos
LAWS OF MOTION
- BOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Short Answer Questions26videos
LAWS OF MOTION
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 NCERT Comprehension4videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks5videos
MATHEMATICAL TOOLS
Similar Questions
Give the magnitude and direction of the net force acting on
(a) a drop of rain falling down with a constant speed
(b) a crok of mass 10 g floating on water
(c) a kit skilfully held stationary in the sky
(d) a car moving with a constant velocity of 30kh/h on a rough road
(e) a high speed electron in space for from all gravitational obects and free of electric and magnetic fields.02:35View SolutionA stone of mass 0.2 kg is tied to one end of a string of length 80cm Holding the other end, the stone is wirled into a vertical circle. What is the minimum speed of the stone at the lowest point so that it just completes the circle What is the tension in the string at the lowest point of the circular path ? . (g=10−2) .
05:44View SolutionThe minimum force required just to move a block on a rough horizontal surface is 10 N An applied force of 5 N fails to move the block. What are the values of static friction and dynamic friction ?
03:29View SolutionWhen a body is subjected to a uniform acceleratuib, it alwaus moves in a straight line.
Straight line motion is the natural tendency of the body.01:54View Solution(a+b)2+(a−b)2=….
02:49View SolutionTwo blocks of masses m_(1) and m_(2) are connected through a massless inextensible string .A block of mass m_(1) is placed at the fixed rigid inclined surface while the block of mass m_(2) hanging at the other end of the string which is passing through a fixed massless frictionless pulley shown in figure The coefficient of static friction between the block and the inclined plane is 0.8 The system of masses m_(1) and m_(2) released from rest
04:00View SolutionA system consists of three masses m1 , m1 , m1 , m2 and m3 connected by a string passing over a pulley P . The mass m1 hangs freely and m2 and m3 are on a rough horizontal table (the coefficient of friction=μ) The pulley is frictionless and of negligible mass. The (Assume m1=m2=m3=m).
 04:00View Solution
04:00View SolutionTwo masses m1 and m2 are attached to the ends of a massless string which passes over a frictionless pulley attached to the top of an inclined plane. The angle of inclination of the plane is θ. Take g=10ms−2
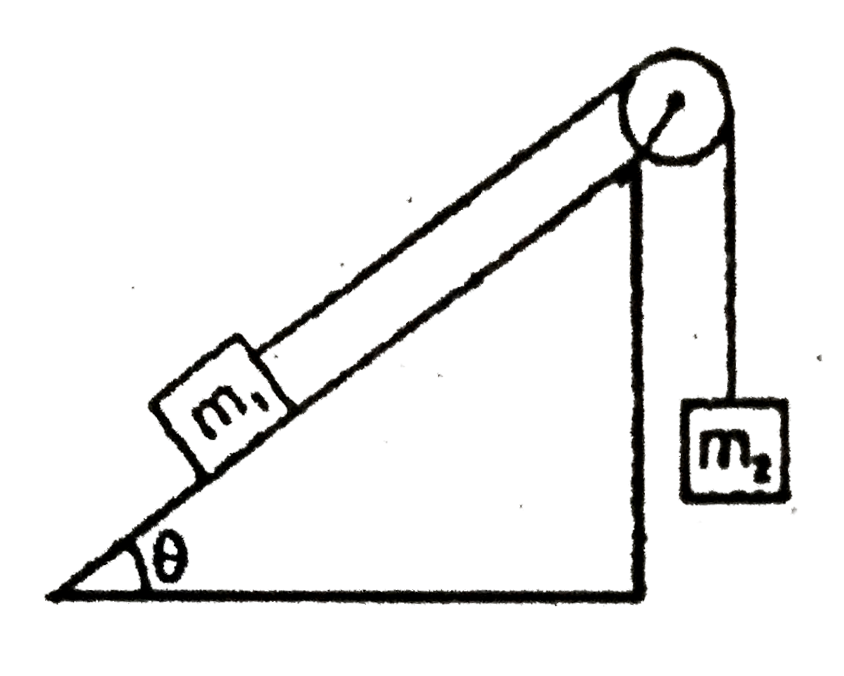
if m1=10kg,m2=5kg,θ=30∘, what is the acceleration of mass m2?View SolutionTwo masses M_(1) " and " M_(2) are attached to the ends of a string which passes over a pulley attached to the top of an inclined plane. The angle of inclination of the plane is 30^(@) and M_(1)=10 kg, M_(2)=5kg . What is the acceleration of mass M_(2) ?
04:14View SolutionA system consists of three masses m_(1),m_(2) " and " m_(3) connected by a string passing over a pulley P. The mass m_(1) hangs freely and m_(2) " and " m_(3) are on a rough horizontal table (the coefficient of friction= mu ). The pulley is frictionless and of negligible mass. The downward acceleration of mass m_(1) is (assume, m_(1)=m_(2)=m_(3)=m )
10:06View SolutionA wire of 9.8×10−3kg per meter mass passes over a fricationless pulley fixed on the top of an inclined frictionless plane which makes an angle of 30∘ with the horizontal. Masses M1 & M2 are tied at the two ends of the wire. The mass M1 rests on the plane and the mass M2 hangs freely vertically downwards. the whole system is in equilibrium. Now
01:49View SolutionTwo masses m_(1) and m_(2) ( m_(2) gt m_(1)) are hanging vertically over frictionless pulley. The acceleration of the two masses is :
05:18View SolutionTwo masses M_(1) and M_(2) are attached to the ends of string which passes over the pulley attached to the top of a double inclined plane. The angles of inclination of the inclined planes are alpha and beta . Take g=10ms^(-2) . If M_(1)=M_(2) and alpha=beta , what is the acceleration of the system?
04:21View SolutionA system consists of three masses m1m2 and m3 connected by a string passing over a pulley P. The mass m1 hangs freely and m2 and m3 are on a rough horizontal table (the co efficient of fircition = p). The pulley is frictionless and of negligible mass. The downward acceleration of mass m1 is (Assumem1−m2=m3=m)
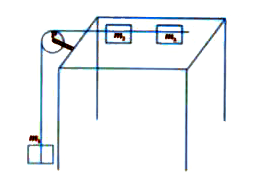 02:12View Solution
02:12View SolutionA system consists of three masses m1,m2 and m3 connected by a string passing over a pulley P. The mass m1 hangs freely and m2 and m3 are on a rough horizontal table (the coefficient of friction=μ). The pulley is frictionless and of negligible mass. The downward acceleration of mass m1 is (assume, m1=m2=m3=m)
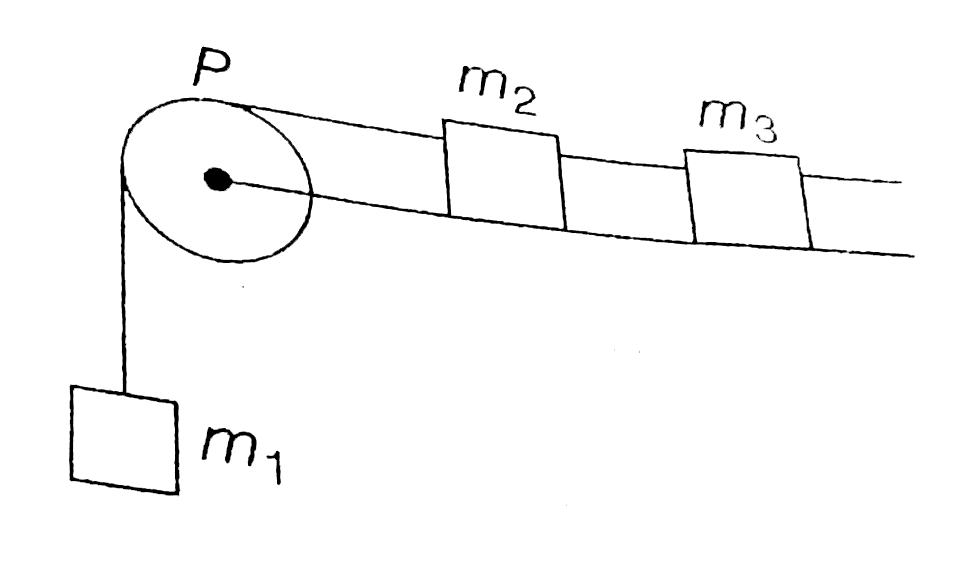 02:59View Solution
02:59View Solution

