A wooden block of mass M resting on a rough horizontal surface is pulled with a force T at an angle q to the horizontal. If m is coefficient of kinetic friction between the block and the surface, the acceleration of the block is
TcosθM−μg
Tm(cosθ−sinθ)−μg
Tm(cosθ−μsinθ)−μg
μTcosθM−μg
The correct Answer is:C
To find the acceleration of a wooden block of mass M being pulled with a force T at an angle θ to the horizontal on a rough surface, we can follow these steps:
Step 1: Analyze the Forces Acting on the Block
The forces acting on the block include:
- The gravitational force W=Mg acting downward.
- The normal force N acting upward.
- The pulling force T at an angle θ which can be resolved into two components:
- Horizontal component: Tcosθ
- Vertical component: Tsinθ
- The frictional force f acting opposite to the direction of motion.
Step 2: Write the Equation for the Vertical Forces
In the vertical direction, the forces must balance. Thus, we have:
N+Tsinθ=Mg
From this equation, we can express the normal force N:
N=Mg−Tsinθ
Step 3: Write the Equation for the Frictional Force
The frictional force f can be expressed as:
f=μN=μ(Mg−Tsinθ)
where μ is the coefficient of kinetic friction.
Step 4: Write the Equation for the Horizontal Forces
In the horizontal direction, the net force acting on the block is given by the difference between the horizontal component of the pulling force and the frictional force:
Tcosθ−f=Ma
Substituting the expression for f:
Tcosθ−μ(Mg−Tsinθ)=Ma
Step 5: Rearranging the Equation
Now, rearranging the equation gives:
Tcosθ−μMg+μTsinθ=Ma
Combining the terms involving T:
(Tcosθ+μTsinθ)−μMg=Ma
Step 6: Solve for Acceleration a
Now, we can isolate a:
a=Tcosθ+μTsinθ−μMgM
Final Expression for Acceleration
Thus, the acceleration a of the block is given by:
a=Tcosθ+μTsinθ−μMgM
The forces acting on the block include:
- The gravitational force W=Mg acting downward.
- The normal force N acting upward.
- The pulling force T at an angle θ which can be resolved into two components:
- Horizontal component: Tcosθ
- Vertical component: Tsinθ
- The frictional force f acting opposite to the direction of motion.
In the vertical direction, the forces must balance. Thus, we have:
N+Tsinθ=Mg
From this equation, we can express the normal force N:
N=Mg−Tsinθ
The frictional force f can be expressed as:
f=μN=μ(Mg−Tsinθ)
where μ is the coefficient of kinetic friction.
In the horizontal direction, the net force acting on the block is given by the difference between the horizontal component of the pulling force and the frictional force:
Tcosθ−f=Ma
Substituting the expression for f:
Tcosθ−μ(Mg−Tsinθ)=Ma
Now, rearranging the equation gives:
Tcosθ−μMg+μTsinθ=Ma
Combining the terms involving T:
(Tcosθ+μTsinθ)−μMg=Ma
Now, we can isolate a:
a=Tcosθ+μTsinθ−μMgM
Thus, the acceleration a of the block is given by:
a=Tcosθ+μTsinθ−μMgM
Topper's Solved these Questions
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - MOTION IN A PLANE
87 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )
52 Videos
- ATOMSBOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - PRACTICE EXERCISE
21 Videos
Similar Questions
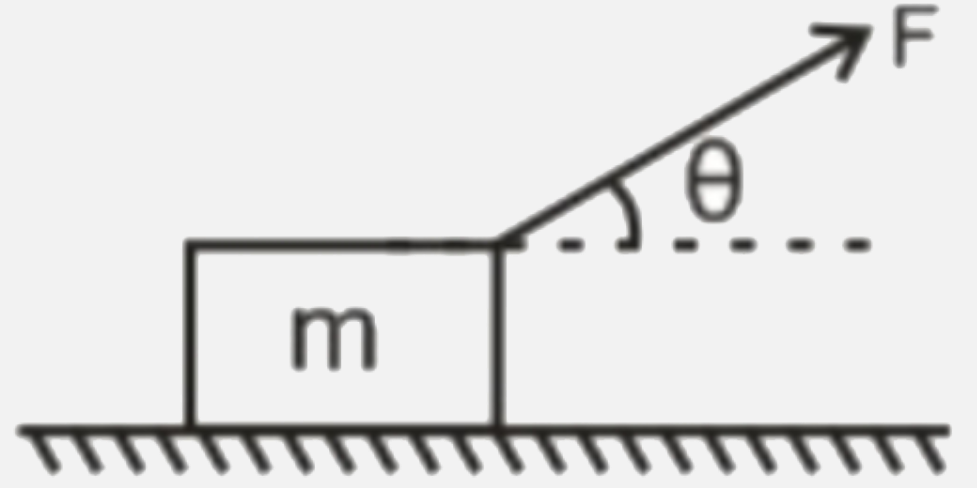
A wooden block of mass m resting on a rough horizontal table is pulled by a force F as shown in the figure. If μ is the coefficient of friction between block and table, its acceleration will be
View SolutionA block of weight 200N is pulled along a rough horizontal surface at constant speed by a force 100N acting at an angle 30∘ above the horizontal. The coefficient of friction between the block and the surface is
View Solution
Knowledge Check
A block of mass 3 kg rests on a rough inclined plane making an angle of 30∘. With the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
A9.8 NB0.7×9.8×√3 NC9.8×√3 ND0.7×9.8 NA block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
A10.3NB23.8NC11.9ND6.3N
A block of mass 10 kg is placed on the rough horizontal surface. A pulling force F is acting on the block which makes an angle θ above the horizontal. If coefficient of friction between block and surface is 43 then minimum value of force required to just move the block is (g=10ms2)
View SolutionA block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
View SolutionA block of mass m is moving on a rough horizontal surface. μ is the coefficient of kinetic friction between the block and the surface. What is the net force exerted by the surface on the block?
View SolutionA block of mass M is pulled along a horizontal surface by applying a force at angle θ with the horizontal. The friction coefficient between the block and the surface is μ. If the block travels at a uniform velocity, find the work done by this applied force during a displacement d of the block.
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal. If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View SolutionA block of mass M is pulled along a horizontal surface by applying a force at angle θ with the horizontal. The friction coefficient between the block and the surfasce is μ. If the block travels at a uniform velocity, find the work donen by this applied force during a displacement d of the blcok.
View Solution