A particle of mass m is acted upon by a force F given by the emprical law F=Rt2υ(t)
If this law is to be tested experimentally by observing the motion starting from rest, the best way is to plot :
log υ (t) given 1t
υ(t) against t2
log υ (t) given 1t2
logυ(t) against t
The correct Answer is:A
Step by step video & image solution for A particle of mass m is acted upon by a force F given by the emprical law F=(R)/(t^2)upsilon(t) If this law is to be tested experimentally by observing the motion starting from rest, the best way is to plot : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - MOTION IN A PLANE
87 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )
52 Videos
- ATOMSBOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - PRACTICE EXERCISE
21 Videos
Similar Questions
A particle of mass m is acted upon by a force F=t2−kx . Initially , the particle is at rest at the origin. Then
View SolutionA block of mass m at rest is acted upon by a force F for a time t. The kinetic energy of block after time t is
View SolutionThe velocity →v of a particle of mass 'm' acted upon by a constant force is given by →v(t)=A[cos(kt)¯i−sin(kt)¯j] . Then the angle between the force and the momentum of the particle is (Here A and k are constants)
View SolutionA particle is acted upon by a force given by F=(12t−3t2)N, where is in seconds. Find the change in momenum of that particle from t=1 to t=3 sec.
View SolutionPassage XII)_ A particle of mass m is constrained to move along x-axis. A force F acts on the particle. F always points toward the position labelled E. For example, when the particle is to the left of E,Fpoints to the right. The magnitude of F is consant except at point E where it is zero. The systm is horizontal. F is the net force acting on the particle. the particle is displaced a distance A towards left from the equilibrium position E and released from rest at t=0.
What it is the time period of periodic motion of particle.
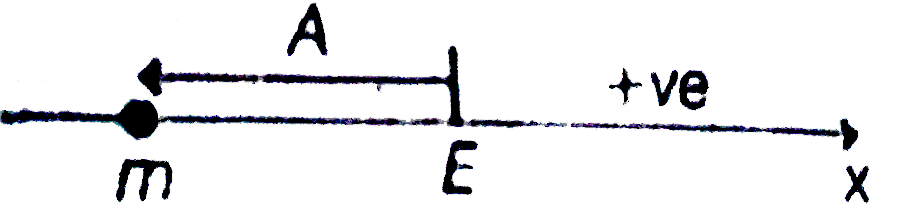
View SolutionPassage XII)_ A particle of mass m is constrained to move along x-axis. A force F acts on the particle. F always points toward the position labelled E. For example, when the particle is to the left of E,Fpoints to the right. The magnitude of F is consant except at point E where it is zero. The systm is horizontal. F is the net force acting on the particle. the particle is displaced a distance A towards left from the equilibrium position E and released from rest at t=0.
Velocity-time graph of the particle is
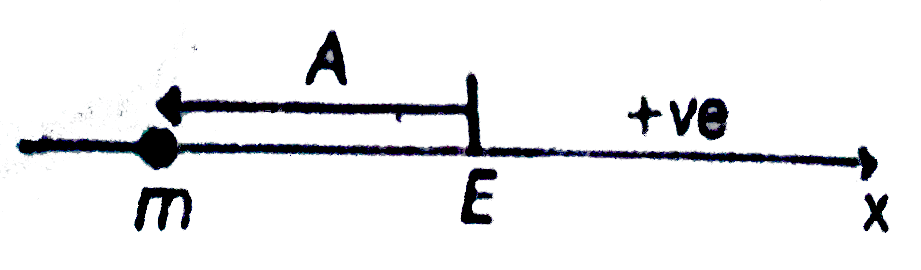
View SolutionA particle of mass m initially at rest is acted upon by a unidirectional force F=F∘cos(π2t). The distance travelled by the particle when it stops first in the subsequent motion is ,
View SolutionA particle of mass m initially at rest. A variabl force acts on the particle f=kx2 where k is a constant and x is the displacment. Find the work done by the force f when the speed of particles is v.
View SolutionA particle of mass m is driven by a machine that delivers a constant power k watts. If the particle starts from rest the force on the particle at time t is
View SolutionA particle of mass 70 g, moving at 50 cm/s , is acted upon by a variable force opposite to its direction of motion. The force F is shown as a function of time t
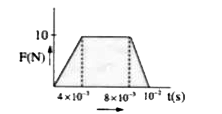
(a) its speed will be 50 cm/s after the force stops acting
(b) its direction of motion will reverse
(c) its average acceleration will be 1m/s2 during the interval in which the force acts
its average acceleration will be 10m/s2 during the interval in which the force acts
View Solution
