A wooden plank of length 1m and uniform cross-section is hinged at one end to the bottom of a tank as shown in fig. The tank is filled with water upto a hight 0.5m. The specific gravity of the plank is 0.5. Find the angle θ that the plank makes with the vertical in the equilibrium position. (Exclude the case θ=θ∘)
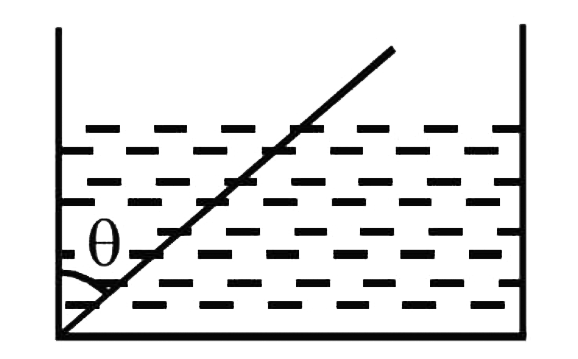
Let A : area of cross-section of rod
L : length of rod
σ : density of material of rod
Weight of plank W=σALg (vertically upward). Acting at distance 12(hcosθ)fromO.
Taking torque about O (net torque =0)
W×L2sinθ=FB×12hcosθsinθ
σALg(L2)sinθ=ρωAhcosθg.h2cosθsinθ
σ=0.5gm/cc,L=1m,ρω=1gm/cc,h=0.5m
0.5=(0.5)2cos2θ⇒cos2θ=0.5=12
cosθ=1√2⇒θ=4.5∘.
 .
.
Topper's Solved these Questions
Similar Questions
The wooden plank of length 1 m and uniform cross section is hinged at one end to the bottom of a tank as shown in figure. The tank is filled with water up to a height of 0.5 m. The specific gravity of the plank is 0.5. Find the angle θ that the plank makes with the vertical in the equilibrium position. (Exclude the case θ=0)
 ,View Solution
,View SolutionA wooden plank of length 1m and uniform cross-section is hinged at one end of the bottom of tank as shown in figure. The tank is filled with water upto a height of 0.5m. Find the angle θ that the plank makes with the vertical in the equilibrium position. [Exclude the case thea=0]
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A wooden rod of a uniform cross section and of length 120cm is hinged at the bottom of the tank which is filled with water to a height of 40cm. In the equilibrium position, the rod makes an angle of 60∘ with the vertical. The centre of buoyancy is located on the rod at a distance (from the hinge) of
A20cmB40cmC60cmD75cm - Question 2 - Select One
A uniform rod of length 2.0 m specific gravity 0.5 and mass 2 kg is hinged at one end to the bottom of a tank of water (specific gravity = 10) filled upto a height o f 1.0 m as shown in figure. Taking the case θ=−0∘ the force exerted by the hings on the rod is (g=10m/s2)
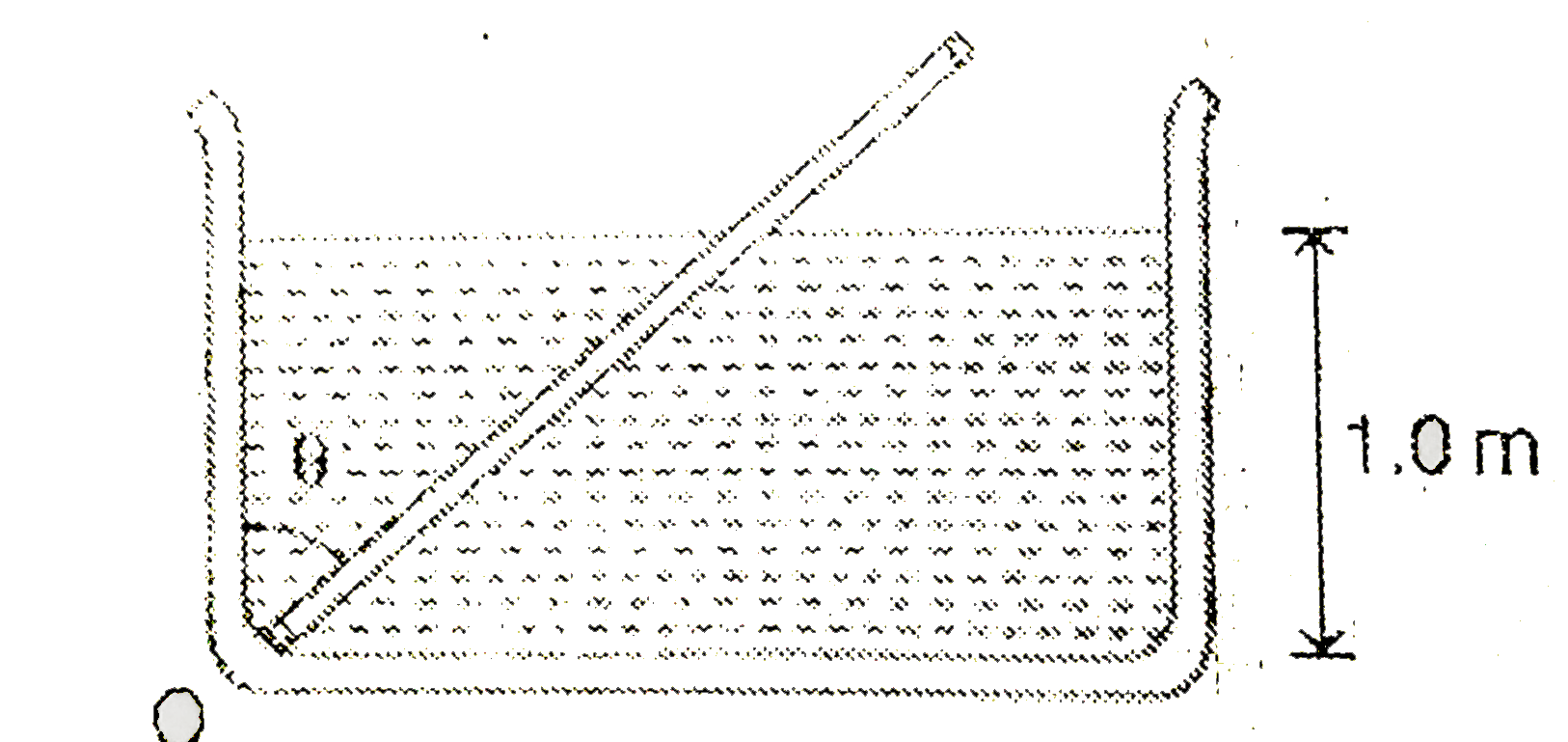 A10.2 N upwardsB4.2 N downwardsC8.3 N downwardsD6.2 N upwards
A10.2 N upwardsB4.2 N downwardsC8.3 N downwardsD6.2 N upwards
Two non-viscous, incomoressible and immiscible liquids of densities ρ and 1.5ρ are poured into the two limbs of a circules tube of radius R and small cross-section kept fixed in a vertical plane as shown in fig. Each liquid occupies one-fourth the cirumference of the tube.

(a) Find the angle θ the radius to the interface makes with the vertical in equilibrium position.
(b) If the whole liquid column is given a small displacement from its equilibrium position, show that the resulting oscillations alre simple harmonic. Find the time period of these oscillations.View SolutionTwo non-viscous, incompressible and immiscible liquids of densities p and 1.5p are poured into the two limbs of a circular tube of radius R and small cross section kept fixed in a vertical plane as shown in the figure. Each liquid occupies one fourth the circumference of the tube.
(i)Find the angle theta that the radius to the interface makes with the vertical in equilibrium position. _________
(ii) If the whole liquid column is given a small displacement from its equilibrium position, show that the resulting oscillations are simple harmonic. Find the time period of these oscillations. ____________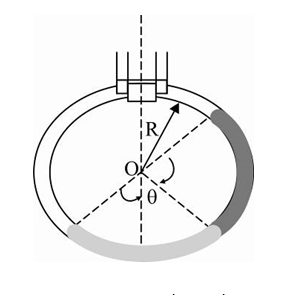 View Solution
View SolutionA tank of square cross section (2m×2m) is filled with water up to a height of 2.5m. Find the thrust experienced by the vertical and botom of the tank (g=10m/s2).
View SolutionA uniform wooden bar of length l and mass m hinged on a vertical wall of a containing water, at one end.

3/5th part of the bar is submerged in water. Find the ratio of densities of the liquid and the bar.View SolutionA box of mass 4 kg is placed on a wooden plank of length 1.5m which is lying on the ground. The plank is lifted from one end along its length so that it becomes inclined. It is noted that when the vertical height of the top end of the plank from the ground becomes 0.5m, the box begins to slide. Find the coefficient of friction between the box and the plank.
View SolutionA conical pendulum, a thin uniform rod of length l and mass m, rotates uniformly about a vertical axis with angular velocity ω(the upper end of the rod is hinged). Find the angle θ between the rod and the vertical.
View Solution

