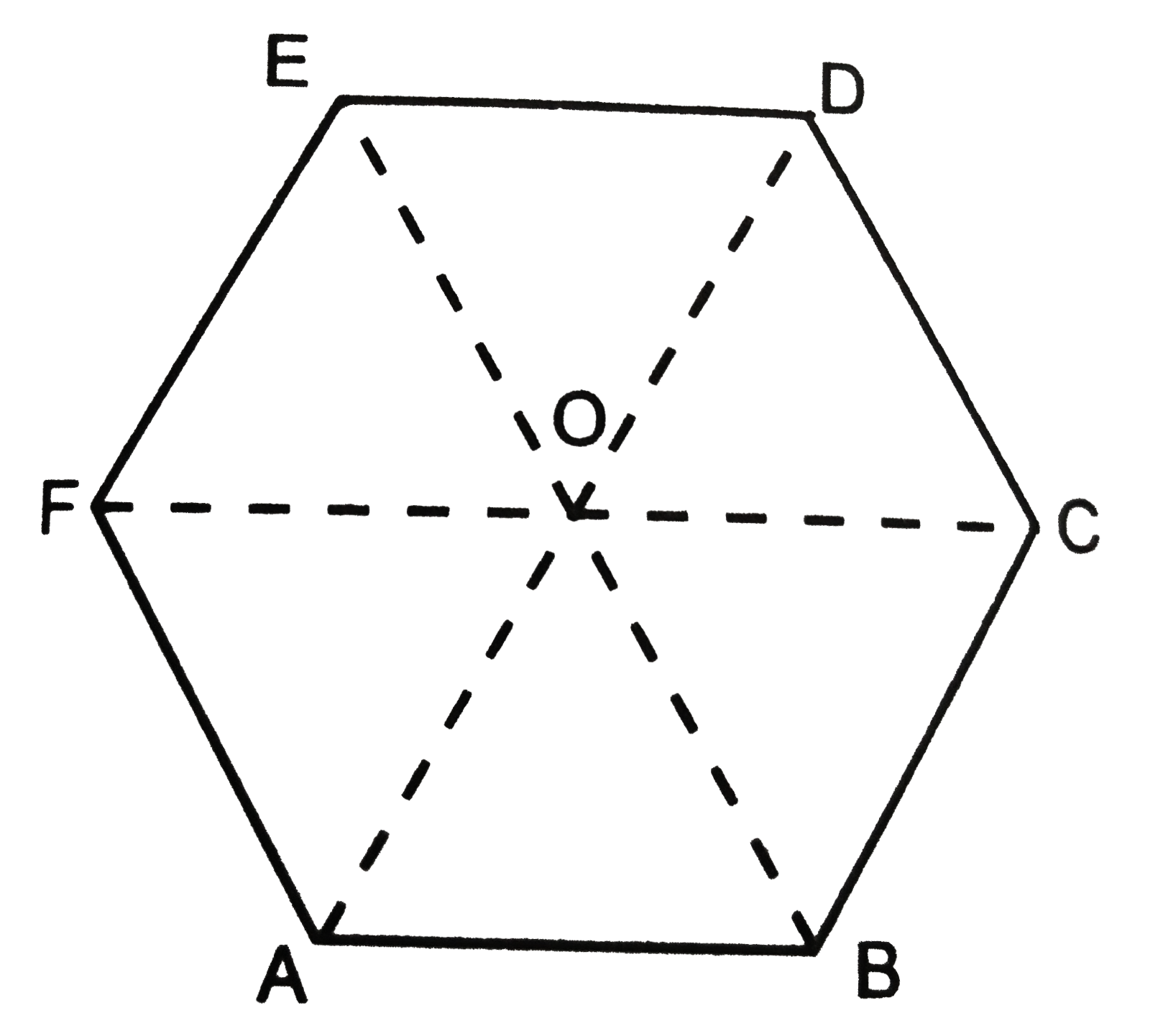
ABCDEF is a regular hexagon with point O as centre. The value of $- - \to A B + - - \to A C + - - \to A D + - - \to A E + - - \to A F$ is

A

$2 - - \to A O$

B

$2 - - \to A O$

C

$6 - - \to A O$

D

0

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:C

To solve the problem of finding the value of $\to A B + \to A C + \to A D + \to A E + \to A F$ for a regular hexagon ABCDEF with center O, we can follow these steps:
Step 1: Understand the Geometry of the Hexagon
A regular hexagon has equal sides and angles. The center O is equidistant from all vertices (A, B, C, D, E, F).
Step 2: Define the Vectors
- $\to A B$ is the vector from point A to point B.
- $\to A C$ is the vector from point A to point C.
- $\to A D$ is the vector from point A to point D.
- $\to A E$ is the vector from point A to point E.
- $\to A F$ is the vector from point A to point F.
Step 3: Express Each Vector in Terms of Center O
Since O is the center:
- $\to A C = \to A B + \to A O$
- $\to A E = \to A F + \to A O$
Step 4: Substitute and Rearrange
Now we can substitute the expressions for $\to A C$ and $\to A E$ :
$\to A B + \to A C + \to A D + \to A E + \to A F = \to A B + (\to A B + \to A O) + \to A D + (\to A F + \to A O) + \to A F$
Step 5: Group Similar Terms
Group the vectors:
$= \to A B + \to A B + \to A O + \to A D + \to A F + \to A O + \to A F$
This simplifies to:
$= 2 \to A B + \to A D + 2 \to A F + 2 \to A O$
Step 6: Analyze the Vectors
Notice that $\to A D$ can be expressed in terms of $\to A O$ as well. Since all vertices are symmetric about the center O, we can express $\to A D$ as $2 \to A O$ (because it goes from A to D, which is two vertices away).
Step 7: Combine the Vectors
Now, substituting $\to A D$ :
$= 2 \to A B + 2 \to A O + 2 \to A F + 2 \to A O$
This simplifies to:
$= 2 \to A B + 2 \to A F + 4 \to A O$
Step 8: Final Summation
Since $\to A B + \to A F$ is equivalent to $\to A O$ (as they are symmetric), we can write:
$= 2 \to A O + 4 \to A O = 6 \to A O$
Conclusion
Thus, the value of $\to A B + \to A C + \to A D + \to A E + \to A F$ is:
$6 \to A O$

|

Updated on:7/8/2024

Class 11 PHYSICS VECTOR

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Consider the ragular hexagon ABCDEF with centre at O (origin).
Five forces $- - \to A B, - - \to A C, - - \to A D, - - \to A E, - - \to A F$ act at the vertex A of a regular hexagon ABCDEF. Then their resultant is
A $3 - - \to A O$
B $2 - - \to A O$
C $4 - - \to A O$
D $6 - - \to A O$
Question 2 - Select One
Let O be the centre of a regular pentagon ABCDE and $- - \to O A = \to a$ , then $- - \to A B + - -- \to 2 B C + - -- \to 3 C D + - -- \to 4 D E + - -- \to 5 E A$ is equals:
A0
B $4 \to a$
C $5 \to a$
D $6 \to a$
Question 3 - Select One
Let O be the centre of a regular pentagon ABCDE and $- - \to O A = \to a$ , then $- - \to A B + - -- \to 2 B C + - -- \to 3 C D + - -- \to 4 D E + - -- \to 5 E A$ is equals:
A $6 \to a$
B $5 \to a$
C $4 \to a$
D $\to 0$

CENGAGE PHYSICS-VECTORS-Exercise Single Correct

Home
Ask Doubt
Profile