An air -filled parallel-plate capacitor is to be constructed which can store12μC of charge when operated at 1200V.What can be the minimum plate area of the capacitor?The dielectric strength air is 3×106Vm−1.
To solve the problem step by step, we will follow the reasoning laid out in the video transcript.
Step 1: Understand the Given Information
We have:
- Charge (Q) = 12 µC = 12×10−6 C
- Voltage (V) = 1200 V
- Dielectric strength of air (E) = 3×106 V/m
Step 2: Use the Formula for Capacitance
The capacitance (C) of a parallel-plate capacitor can be expressed in two ways:
1. C=ϵ0AD (where A is the area of the plates and D is the separation between them)
2. C=QV
Step 3: Relate Electric Field and Plate Separation
The electric field (E) between the plates is given by:
E=VD
From this, we can express the separation D as:
D=VE
Step 4: Substitute D into the Capacitance Formula
Substituting D from Step 3 into the capacitance formula from Step 2:
C=ϵ0AD
becomes:
C=ϵ0AEV
Step 5: Rearranging for Area A
From the second expression for capacitance C=QV, we can set the two expressions for capacitance equal to each other:
QV=ϵ0AEV
Cancelling V from both sides gives:
Q=ϵ0AE
Rearranging for area A:
A=Qϵ0E
Step 6: Substitute Known Values
Now we can substitute the known values into the area formula:
- Q=12×10−6 C
- ϵ0=8.85×10−12 F/m
- E=3×106 V/m
Thus:
A=12×10−68.85×10−12×3×106
Step 7: Calculate the Area
Calculating the denominator:
8.85×10−12×3×106=2.655×10−5
Now substituting back:
A=12×10−62.655×10−5
A≈0.452m2
Final Answer
The minimum plate area of the capacitor is approximately:
A≈0.45m2
---
We have:
- Charge (Q) = 12 µC = 12×10−6 C
- Voltage (V) = 1200 V
- Dielectric strength of air (E) = 3×106 V/m
The capacitance (C) of a parallel-plate capacitor can be expressed in two ways:
1. C=ϵ0AD (where A is the area of the plates and D is the separation between them)
2. C=QV
The electric field (E) between the plates is given by:
E=VD
From this, we can express the separation D as:
D=VE
Substituting D from Step 3 into the capacitance formula from Step 2:
C=ϵ0AD
becomes:
C=ϵ0AEV
From the second expression for capacitance C=QV, we can set the two expressions for capacitance equal to each other:
QV=ϵ0AEV
Cancelling V from both sides gives:
Q=ϵ0AE
Rearranging for area A:
A=Qϵ0E
Now we can substitute the known values into the area formula:
- Q=12×10−6 C
- ϵ0=8.85×10−12 F/m
- E=3×106 V/m
A=12×10−68.85×10−12×3×106
Calculating the denominator:
8.85×10−12×3×106=2.655×10−5
Now substituting back:
A=12×10−62.655×10−5
A≈0.452m2
The minimum plate area of the capacitor is approximately:
A≈0.45m2
Topper's Solved these Questions
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - short answer
7 Videos
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE 2
6 Videos
- BOHR'S MODEL AND PHYSICS OF THE ATOMBOOK - HC VERMA ENGLISHCHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Short Answer
10 Videos
- DISPERSION AND SPECTRABOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer
6 Videos
Similar Questions
What is the largest charge a metal ball of 1 mm radius can hold ? (Dielectric strength of air is 3×106Vm−1)
View SolutionA parallel plate capacitor is constructed with plates of area 0.0280m2 and separation 0.550mm. Find the magnitude of the charge on each plate of this capacitor when the potential between the plates is 20.1V

View SolutionA air filled parallel plate capacitor having circular plates of diameter D is given a charge Q.The magnitude of the force acting between plates is
View SolutionA parallel-plate capacitor having plate are 100cm2 and separation 1.0 mm holds a charge of 0.12μC when connected to a 120 V battery. Find the dielectric constant of the material filling the gap.
View SolutionA parallel plate capacitor has an electric field of 105V/m between the plates. If the charge on the capacitor plate is 1μC, then force on each capacitor plate is-
View SolutionA parallel plate capacitor, with plate area A and plate separation d, is filled with a dielectric slabe as shown. What is the capacitance of the arrangement ?
View SolutionA parallel plate capacitor is filled with a uniform dielectric , maximum charge that can be given to it does not depends upon
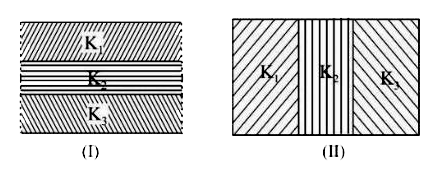
View SolutionTwo identical parallel plate capacitors, of capacitance C each, have plates of area A, separated by a distance d. The space between the plates of the two capacitors, is filled with three dielectrics, of equal thickness and dielectric constants K1,K2andK3. The first capacitor is filled as shown in fig. I, and the second one is filled as shown in fig. II. If these two modified capacitors are charged by the same potential V, the ratio of the energy stored in the two, would be (E1 refers to capacitor (I) and E2 to capacitor (II)):
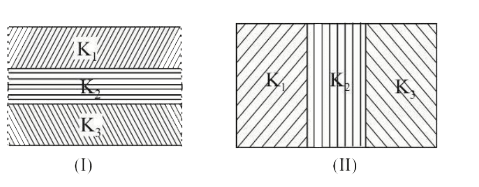
View SolutionTwo identical parallel plate capacitors, of capacitance C each, have plates of area A, separated by a distance d. The space between the plates of the two capacitors, is filled with three dielectrics, of equal thickness and dielectric constants K1,K2andK3.
The first capacitor is filled as shown in fig. I, and the second one is filled as shown in fig. II.
If these two modified capacitors are charged by the same potential V, the ratio of the energy stored in the two, would be ( E1 refers to capacitor (I) and E2 to capacitor (II)):
View SolutionA parallel plate air-core capacitor is connected across a source of constant potential difference. When a dielectric plate is introduced between the two plates then:
View Solution
