A air filled parallel plate capacitor having circular plates of diameter D is given a charge Q.The magnitude of the force acting between plates is
The correct Answer is:4
To find the magnitude of the force acting between the plates of an air-filled parallel plate capacitor with circular plates of diameter D and charge Q, we can follow these steps:
Step 1: Understand the Formula for Force
The force F between two charged plates of a capacitor can be expressed as:
F=Q22Aϵ0
where A is the area of one of the plates and ϵ0 is the permittivity of free space.
Step 2: Calculate the Area of the Circular Plates
The area A of a circular plate is given by the formula:
A=πr2
Since the diameter D is given, we can express the radius r as:
r=D2
Substituting this into the area formula gives:
A=π(D2)2=πD24
Step 3: Substitute the Area into the Force Formula
Now, we can substitute the area A back into the force formula:
F=Q22(πD24)ϵ0
This simplifies to:
F=Q22πD24ϵ0=Q2⋅42πD2ϵ0=2Q2πD2ϵ0
Step 4: Final Expression for the Force
Thus, the magnitude of the force acting between the plates of the capacitor is:
F=2Q2πϵ0D2
Conclusion
The final answer for the magnitude of the force acting between the plates of the capacitor is:
F=2Q2πϵ0D2
The force F between two charged plates of a capacitor can be expressed as:
F=Q22Aϵ0
where A is the area of one of the plates and ϵ0 is the permittivity of free space.
The area A of a circular plate is given by the formula:
A=πr2
Since the diameter D is given, we can express the radius r as:
r=D2
Substituting this into the area formula gives:
A=π(D2)2=πD24
Now, we can substitute the area A back into the force formula:
F=Q22(πD24)ϵ0
This simplifies to:
F=Q22πD24ϵ0=Q2⋅42πD2ϵ0=2Q2πD2ϵ0
Thus, the magnitude of the force acting between the plates of the capacitor is:
F=2Q2πϵ0D2
The final answer for the magnitude of the force acting between the plates of the capacitor is:
F=2Q2πϵ0D2
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-C (OBJECTIVE TYPE QUESTIONS (More than one answer))
13 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-D(COMPREHENSION-I)
2 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-B (OBJECTIVE TYPE QUESTIONS (ONLY ONE ANSWER) )
1 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
15 Videos
Similar Questions
Consider a parallel plate capacitor having charge Q. Then,
View SolutionA parallel plate capacitor is charged. If the plates are pulled apart
View SolutionA parallel plate capacitor with circular plates of radius R is being charged as shown. At the instant shown, the displacement current in the region between the plates enclosed between R2 and R is given by
View SolutionImagine a light planet revolving around a very massive star in a circular orbit of radius r with direction T. On what power of r, will the square of time period depends if the gravitational force of attraction between the planet and the star is proportional to r−5/2 .
View SolutionIn a parallel plate capacitor of capacitor 1μF two plates are given charges 2μC and 4μC the potential difference between the plates of the capacitor is
_2019_CBT2_E01_002_Q01.png)
View SolutionA parallel plate capacitor is charged by certain amount of charge Q. The force of interaction between the plates is F0. If region between the plates is filled by a dielectric material, the force of interaction between the plates is F. The correct statement is
View SolutionA parallel plate capacitor is constructed with plates of area 0.0280m2 and separation 0.550mm. Find the magnitude of the charge on each plate of this capacitor when the potential between the plates is 20.1V

View Solution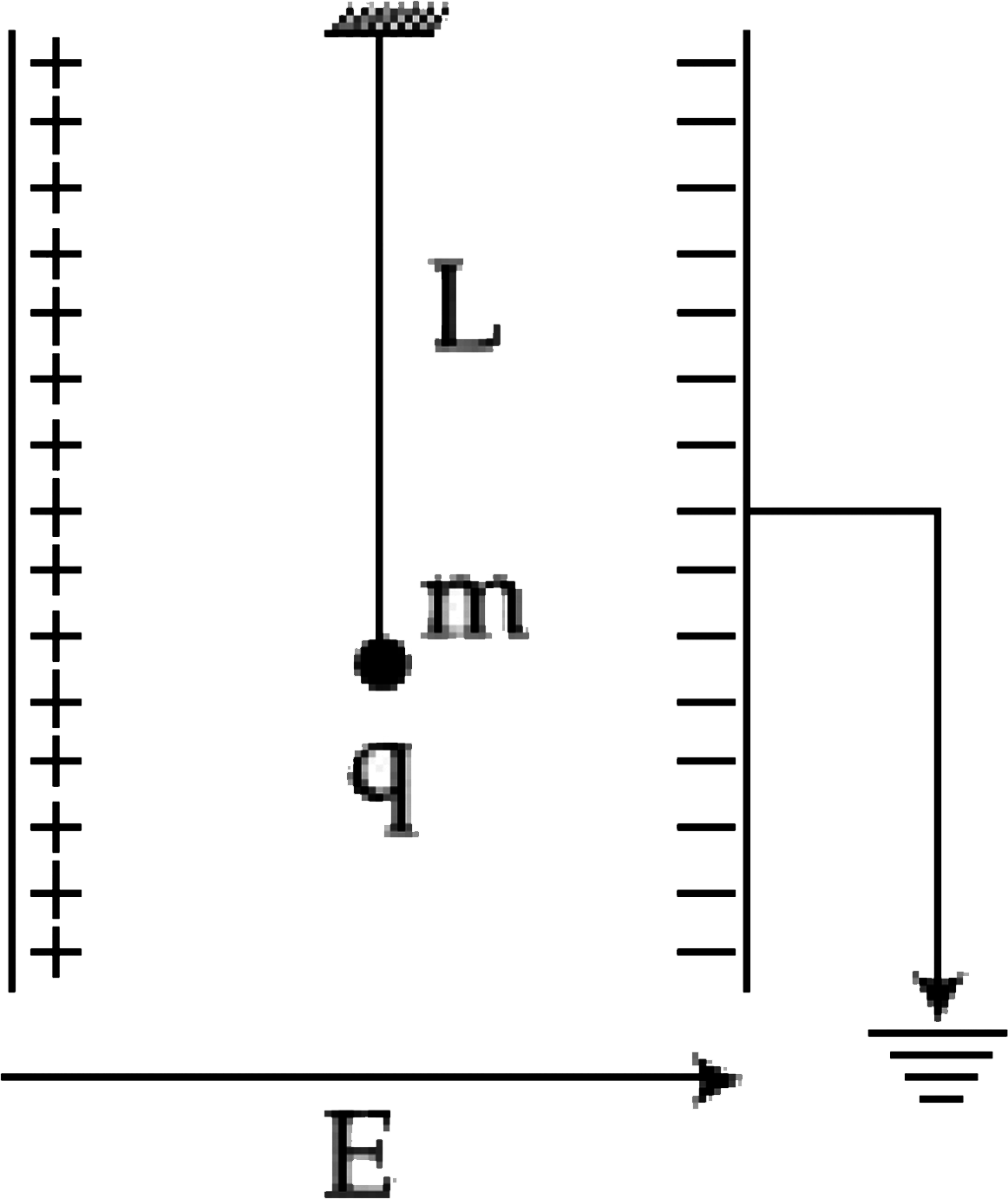
A simple pendulum of length L is placed between the plates of a parallel plate capacitor having electric field E, as shown in figure. Its bob has mass m and charge q. The time period of the pendulum is given by:
View SolutionA simple pendulum of length L is placed between the plates of a parallel plate capacitor having electric field E, as shown in figure. Its bob has mass m and charge q. The time period of the pendulum is given by:
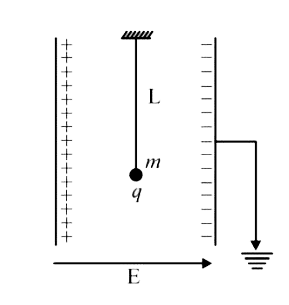
View SolutionA simple pendulum of length L is placed between the plates of a parallel plate capacitor having electric field E, as shown in figure. Its bob has mass m and charge q. The time period of the pendulum is given by:

View Solution
