An alternating current is given by
I=i1cosωt+i2sinωt.
The rms current is given by
i1+i2√2
|i1+i2|√2
√i21+i222
⎷i21+i22√2
The correct Answer is:C
To find the RMS (Root Mean Square) current for the given alternating current I=i1cos(ωt)+i2sin(ωt), we can follow these steps:
Step 1: Identify the components of the current
The given current can be expressed as:
I=i1cos(ωt)+i2sin(ωt)
Here, i1 and i2 are the amplitudes of the cosine and sine components, respectively.
Step 2: Use the trigonometric identity
To combine the two components, we can express the cosine function in terms of sine:
cos(ωt)=sin(ωt+π2)
Thus, we can rewrite the equation as:
I=i1sin(ωt+π2)+i2sin(ωt)
Step 3: Combine the sine terms
Using the sine addition formula, we can combine these terms into a single sine function:
I=√i21+i22sin(ωt+ϕ)
where ϕ is the phase difference between the two components.
Step 4: Calculate the RMS value
The RMS value of a sinusoidal current is given by:
IRMS=Imax√2
where Imax is the maximum (peak) current. In our case, the maximum current is:
Imax=√i21+i22
Thus, substituting this into the RMS formula gives:
IRMS=√i21+i22√2=√i21+i222
Final Result
Therefore, the RMS current is:
IRMS=√i21+i22√2
The given current can be expressed as:
I=i1cos(ωt)+i2sin(ωt)
Here, i1 and i2 are the amplitudes of the cosine and sine components, respectively.
To combine the two components, we can express the cosine function in terms of sine:
cos(ωt)=sin(ωt+π2)
Thus, we can rewrite the equation as:
I=i1sin(ωt+π2)+i2sin(ωt)
Using the sine addition formula, we can combine these terms into a single sine function:
I=√i21+i22sin(ωt+ϕ)
where ϕ is the phase difference between the two components.
The RMS value of a sinusoidal current is given by:
IRMS=Imax√2
where Imax is the maximum (peak) current. In our case, the maximum current is:
Imax=√i21+i22
Thus, substituting this into the RMS formula gives:
IRMS=√i21+i22√2=√i21+i222
Therefore, the RMS current is:
IRMS=√i21+i22√2
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - HC VERMA ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Objective 2
7 Videos
- ALTERNATING CURRENTBOOK - HC VERMA ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercise
19 Videos
- ALTERNATING CURRENTBOOK - HC VERMA ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Workder Examples
8 Videos
- BOHR'S MODEL AND PHYSICS OF THE ATOMBOOK - HC VERMA ENGLISHCHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Short Answer
10 Videos
Similar Questions
If the alternating current I=I1cosωt+I2sinωt, then the rms current is given by
View SolutionThe electric current in a circuit is given by I = 3 sin ωt+4cosωt. The rms current is
View SolutionTwo alternating currents are given by i1=i0sinωtandi2=i0sin(ωt+π3)).
Will the rms values of the currents be equal or different?
View SolutionThe current is given by i=i0+i0 sin omega t then its r.m.s value will be
View SolutionAn alternative current is given by I=(100√2sint)A. The RMS value of current is
View SolutionCurrent in an ac circuit is given by I=3sinωt+4cosωt, then
View SolutionThe voltage and current in a series AC circuit are given by V=V0cosωtandI=i0sinωt.
What is the power dissipated in the circuit?
View SolutionAn alternating current in a circuit is given by l = 20 sin ( 100πt + 0.05π) A. The rms value and the frequency of current respectively are
View SolutionThe electric current in AC circuit is given by the relation i =3sinωt+4cosωt. The rms value of the current in the circuit in ampere is
View SolutionFind the current I in the given circuit
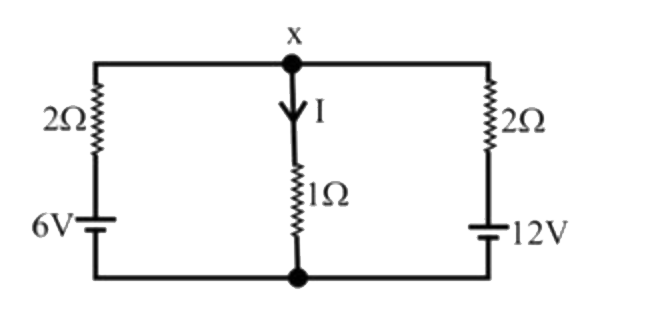
View Solution
