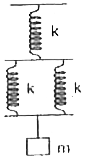
An arrangement of three identical spring and a block of mass 10 kg is shown in the adjoining figure. When the platform on which block is placed is slightly pressed down and released. It performs S.H.M. with a period of 2 s.
(i) Calculate the spring constant of the spring.
(ii) If a block of mass m is further placed on the platform, the new period of S.H.M. becomes 3.5 s. Find the value of m. (Assume platform to be massless)
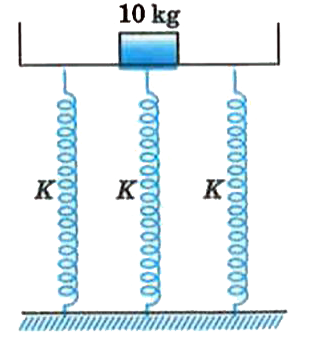
(i) given, spring constant of each spring = K
The three springs are connected in parallel.
∴ Spring constant of combination, K = 3K
M=10kg
now, time period is
T=2π√Mk.
⇒K=4π2MT2=4×9.86×1022
= 98.6 N/m
∴K=K./3=32.87 N/m
= 33 N/m
(ii) When a block of mass m is also placed on the platform, the period of oscillation, will be
T.=2π√m+MK.
∴T.T=√m+MM
Given, T.=3.5s
∴3.52=√m+1010
(1.75)2=m+1010
⇒3.0625×10=m+10
orm=20.625≈21 kg
Topper's Solved these Questions
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - PRACTICE PROBLEMS
15 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - PRACTICE PROBLEMS 2
20 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
Similar Questions
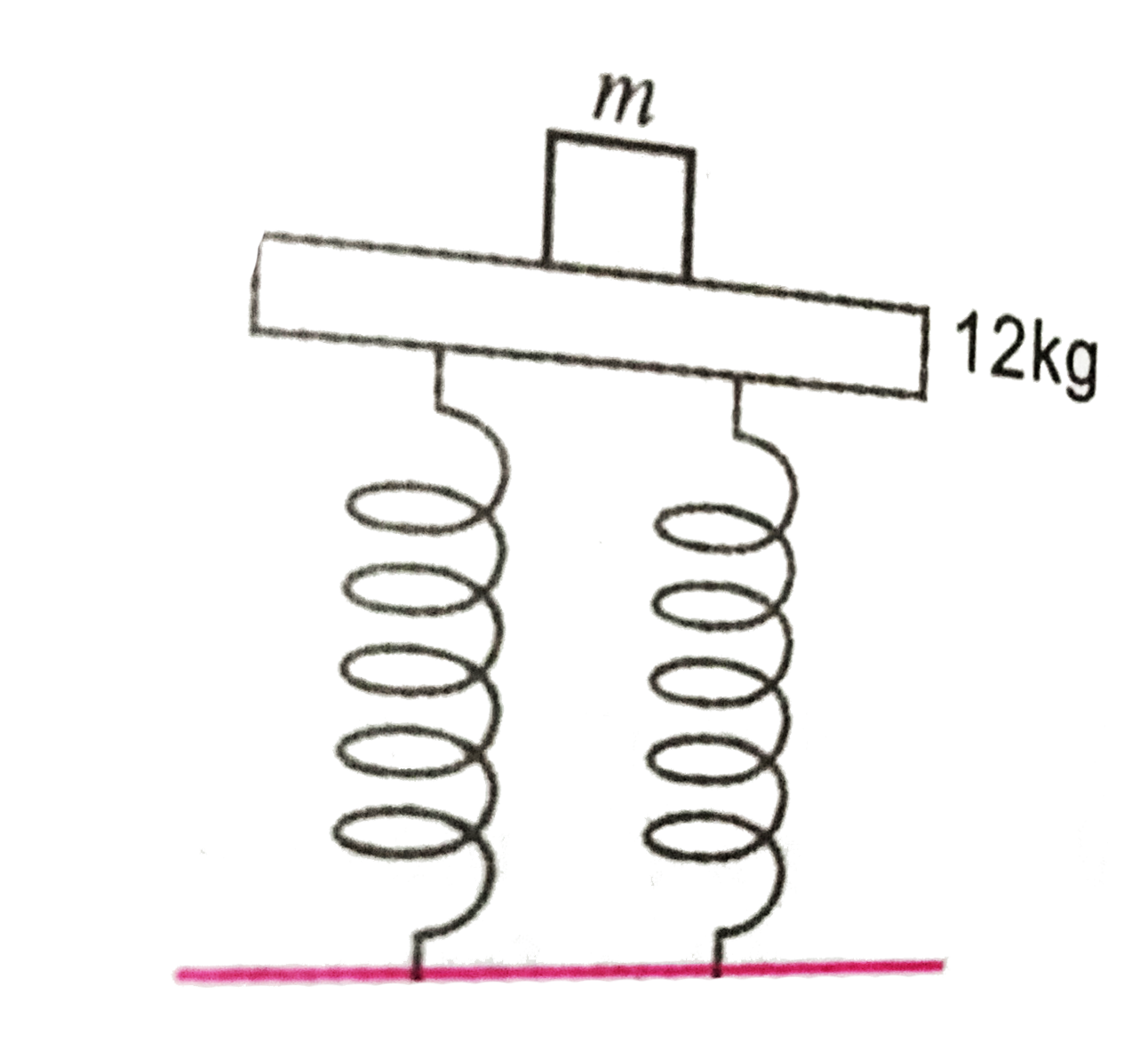
A tray of mass 12 kg is supported by two identical springs as shown in figure. When the tray is pressed down slightly and released, it executes SHM with a time period of 1.5s. What is the force constant of each spring?When a block of mass m is placed on the tray , the period of SHM changes to 3.0s. What is the mass of the block ?
View SolutionA spring mass system has time period of 2 second. What should be the spring constant of spring if the mass of the block is 10grams ?
View Solution
Knowledge Check
A tray of mass M = 10 kg executes SHM of period 1.5s. It is supported on two identical springs of spring constant k as shown in figure. If a block of mass m is also placed on the tray, the period of oscillation increases to 3s. The value of m is:
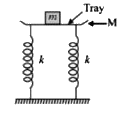 A10 kgB20 kgC30 kgD40 kg
A10 kgB20 kgC30 kgD40 kgA system consists of two spring and a mass m = 1 kg as shown in figure . If mass m is dispalced slightly along vertical and vertical and released. The system oscillates with a period of 2 s .Then , the spring canstant K is
 Aπ24Bπ26Cπ28Dπ22
Aπ24Bπ26Cπ28Dπ22A particle of mass 'm' is attached to three identical springs A,B and C each of force constant 'K' as shown in figure. If the particle of mass 'm' is pushed slightly against the spring 'A' and released the period of oscillations is
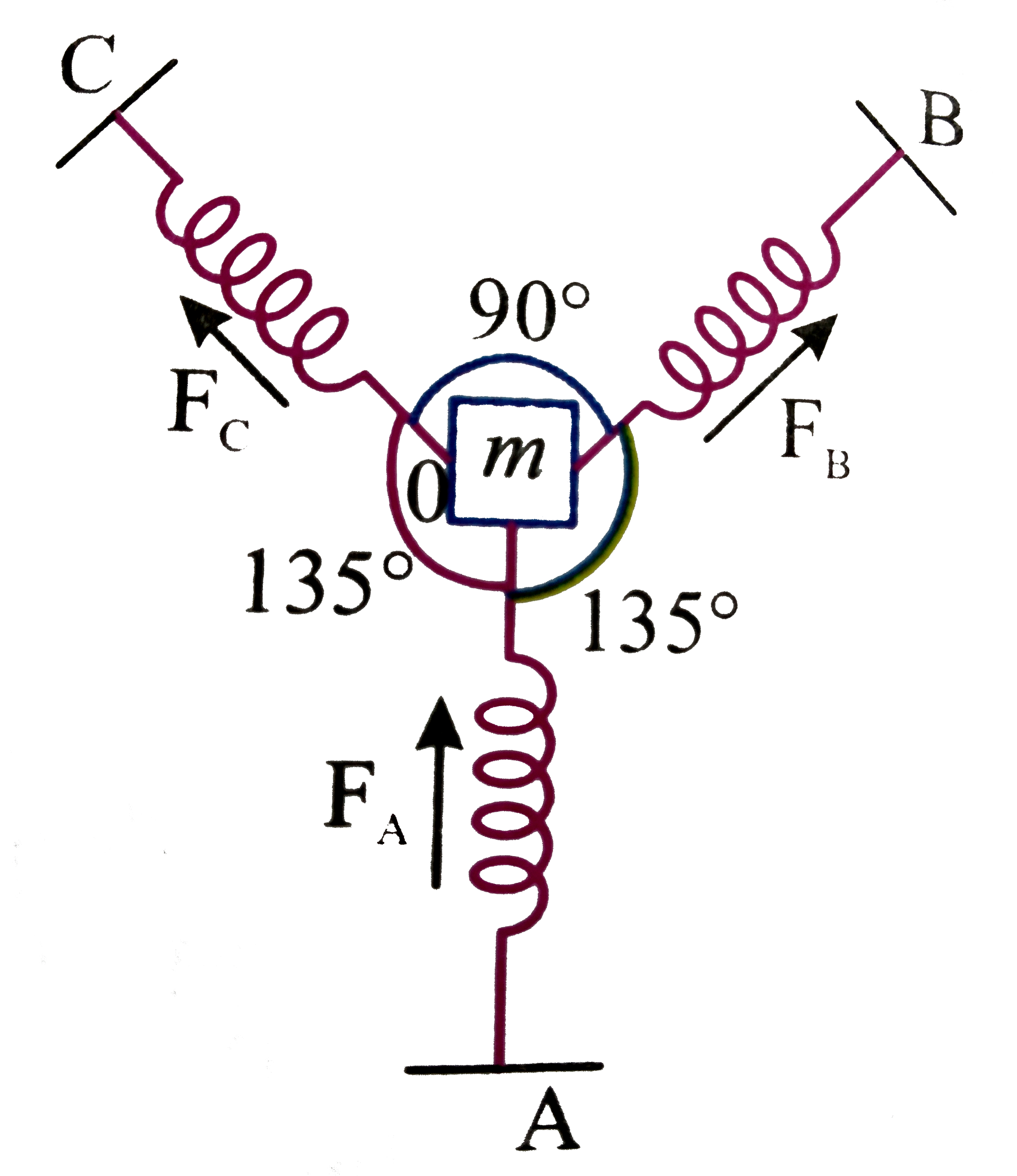 AT=2π√mKBT=2π√2mKCT=2π√m2KDT=π√mK
AT=2π√mKBT=2π√2mKCT=2π√m2KDT=π√mK
A spring mass system has time period of 2 second. What should be the spring constant of spring if the mass of the block is 10grams ?
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View SolutionCalculate the period of oscillations of block of mass m attached with a set of springs as shown
View SolutionA horizontal platform is undergoing vertical S.H>M of time period T. A block of mass M is placed on the platform . The maximum mplitude of the platform so that the block is not detached form it is
View Solution
A plank of mass 12 kg is supported by two identical springs as shown is Fig. The plank always remains horizontal. When the plank is pressed down and released it performs simple harmonic motion with time period 3 s. When a block of m is attached to the plank the time priod changes to 6 s. The mass of the block is
View Solution
