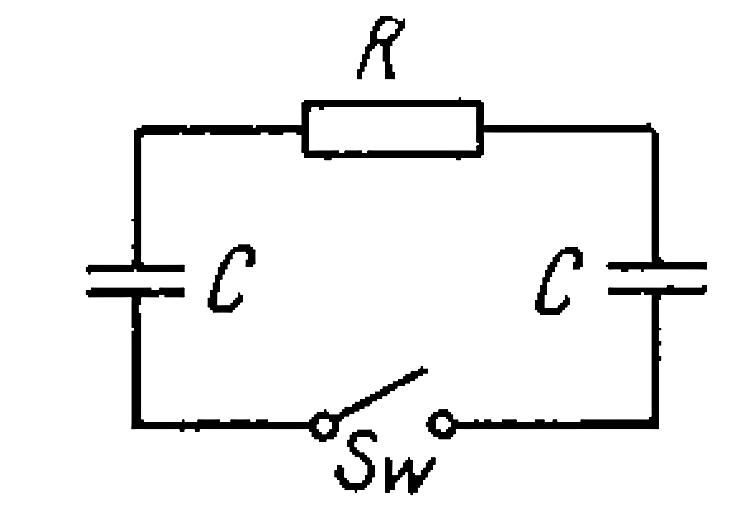
An electric circuit shown in figure has a negligibly small active resistance. The left− hand capacitor was charged to a voltage V0 and then at the moment t=0 the switch Sw was closed. Find the time dependence of the voltages in left and right capacitors.

Initially q1=CV0 and q2=0. After the switch is closed change flows and we get
q1+q2=CV0
q1C+LdIdt−q2C=0 ……..(1)
Also I=.q1=−.q2.Thus
L..I+2IC=0
Hence ..I+ω20I=0 ω20=2LC,
The solution of this equation subject to
I=0 at t=0
is I=I0sinω0t
Integrating q1=A−I0ω0cosω0t
q2=B+I0ω0cosω0t
Finally substituting in (1)
A−BC−2I0ω0Ccosω0t+LI0ω0cosω0t=0
Thus A=B=CV02 and
CV02+I0ω0=0
so q1=CV02(1+cosω0t)
q2=CV02(1−cosω0t)

Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Elastic Waves
39 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise
2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
Knowledge Check
In the circuit shown in figure, Voltage V0 is
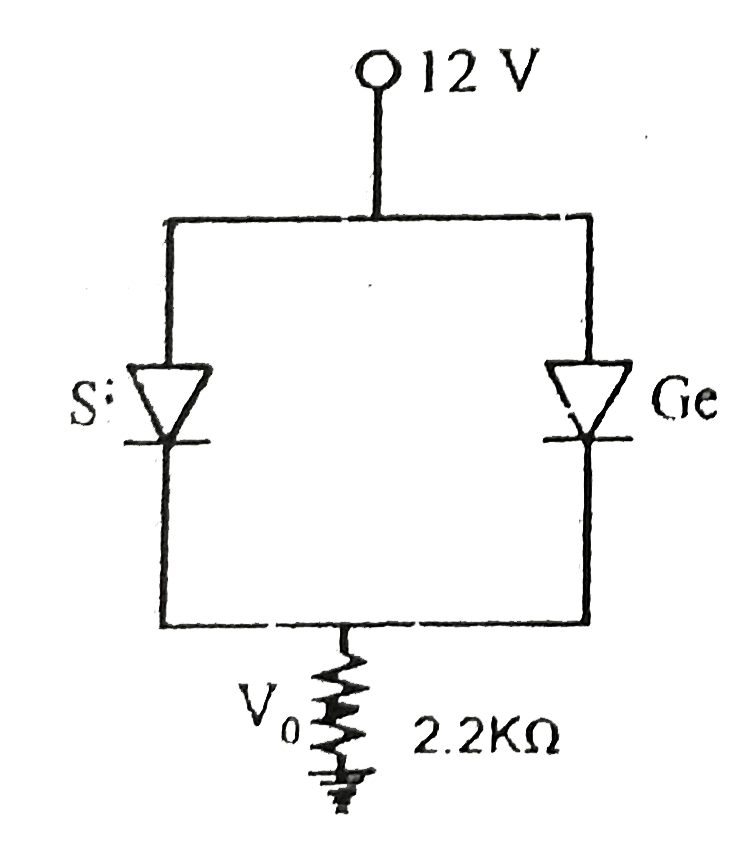 A11.7 voltB11.3 voltC0DNone
A11.7 voltB11.3 voltC0DNoneIn the circuit shown in the figure, the capacitor C is charged to a potential Vo. The heat generated in the circuit when the switch S is closed, is
ACV20B2CV20C4CV20D8CV20At t<0, the capacitor is charged and the switch is opened.At t=0 the switch is closed.The shortest time T at which the charge on the capacitor will be zero is given by:
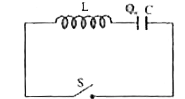 Aπ√LCB32π√LCCπ2√LCD2π√LC
Aπ√LCB32π√LCCπ2√LCD2π√LC
An oscillating circuit consists of a capacitor with capacitance C, a coil of inductance L with negligible resistance, and aswitch. With the switch disconnected , the capacitor was charged to a voltage Vm and then at the moment t=0 the switch was closed . Find :
(a) the current (I(t)) in the circuit as a function of time,
(b) the emf of self- inductance in the coil at the moments when the electric energy of the capacitor is equal to that of the current in the coil.
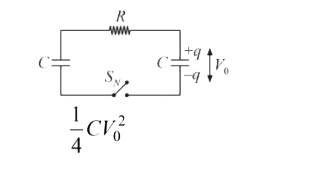
View SolutionIn a circuit shown in fig. the capacitance of each capacitor is equal to C and the resistance, to R One of the capacitor was connected to a voltage V0 and then at the moment t=0 was shorted by means of the swich Sw. Find:
(a) a current I in the circuit as a function of time t:
(b) the amount of generated heat provided a dependence I(t) is known.
View SolutionA circuit consists of a capacitor with capacitance C and a coil of inductance L connected in series, as well as a switch and a resistance equal to the critical value for this circuit. With the switch disconnected, the capacitor was charged to a voltage V0, and at the moment t=0, the switch was closed . Find the corrent I in the circuit as a function of time t.What is Imax equal to ?
View SolutionIn a circuit shown in fig. the capacitance of each capacitor is equal to C and the resistance, to R One of the capacitor was connected to a voltage V0 and then at the moment t=0 was shorted by means of the swich Sw. Find:
(a) a current I in the circuit as a function of time t:
(b) the amount of generated heat provided a dependence I(t) is known.

View SolutionIn a series CR circuit shown in figure,the applied voltage is 10V and the voltage across capacitor is found to be 8V
View Solution