An ideal gas is taken through a quasi-static process described by P=αV2, with α=5.00atm/m6. The gas is expanded to twice its original volume of 1.00m3. How much work is done by the gas in expanding gas in this process?
The correct Answer is:1.18 MJ
To solve the problem of calculating the work done by the gas during its expansion through a quasi-static process described by the equation P=αV2, we will follow these steps:
1. Identify the Given Values:
- The constant α=5.00atm/m6.
- The initial volume V1=1.00m3.
- The final volume V2=2×V1=2.00m3.
2. Convert Pressure Units:
- Convert α from atm to Pascals:
1atm=101325Pa
Therefore,
α=5.00atm/m6=5.00×101325Pa/m6=506625Pa/m6
3. Set Up the Work Integral:
- The work done W by the gas during expansion is given by the integral:
W=∫V2V1PdV
- Substitute P=αV2 into the integral:
W=∫V2V1αV2dV
4. Factor Out the Constant:
- Since α is a constant, we can take it out of the integral:
W=α∫V2V1V2dV
5. Evaluate the Integral:
- The integral of V2 is:
∫V2dV=V33
- Thus, we evaluate from V1 to V2:
W=α(V33)V2V1=α((V2)33−(V1)33)
6. Substitute the Limits:
- Substitute V1=1m3 and V2=2m3:
W=α((2)33−(1)33)=α(83−13)=α(73)
7. Calculate the Work Done:
- Substitute the value of α:
W=506625Pa/m6×73=7×5066253J
- Calculate:
W=35463753J≈1182125J
8. Convert to MegaJoules:
- Finally, convert the work done into MegaJoules:
W≈1.18MJ
Final Answer:
The work done by the gas in expanding is approximately 1.18MJ.
- The constant α=5.00atm/m6.
- The initial volume V1=1.00m3.
- The final volume V2=2×V1=2.00m3.
- Convert α from atm to Pascals:
1atm=101325Pa
Therefore,
α=5.00atm/m6=5.00×101325Pa/m6=506625Pa/m6
- The work done W by the gas during expansion is given by the integral:
W=∫V2V1PdV
- Substitute P=αV2 into the integral:
W=∫V2V1αV2dV
- Since α is a constant, we can take it out of the integral:
W=α∫V2V1V2dV
- The integral of V2 is:
∫V2dV=V33
- Thus, we evaluate from V1 to V2:
W=α(V33)V2V1=α((V2)33−(V1)33)
- Substitute V1=1m3 and V2=2m3:
W=α((2)33−(1)33)=α(83−13)=α(73)
- Substitute the value of α:
W=506625Pa/m6×73=7×5066253J
- Calculate:
W=35463753J≈1182125J
- Finally, convert the work done into MegaJoules:
W≈1.18MJ
The work done by the gas in expanding is approximately 1.18MJ.
Topper's Solved these Questions
- THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - 3
3 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - 4
3 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - 24
1 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Comprehension Type
5 Videos
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct
9 Videos
Similar Questions
A sample of ideal gas is expanded to twice its original volume of 1.00m3 in a quasi-static process for which p=αV2, with α=5.00atm/m6, as shown in Fig. How much work is done by the expanding gas?
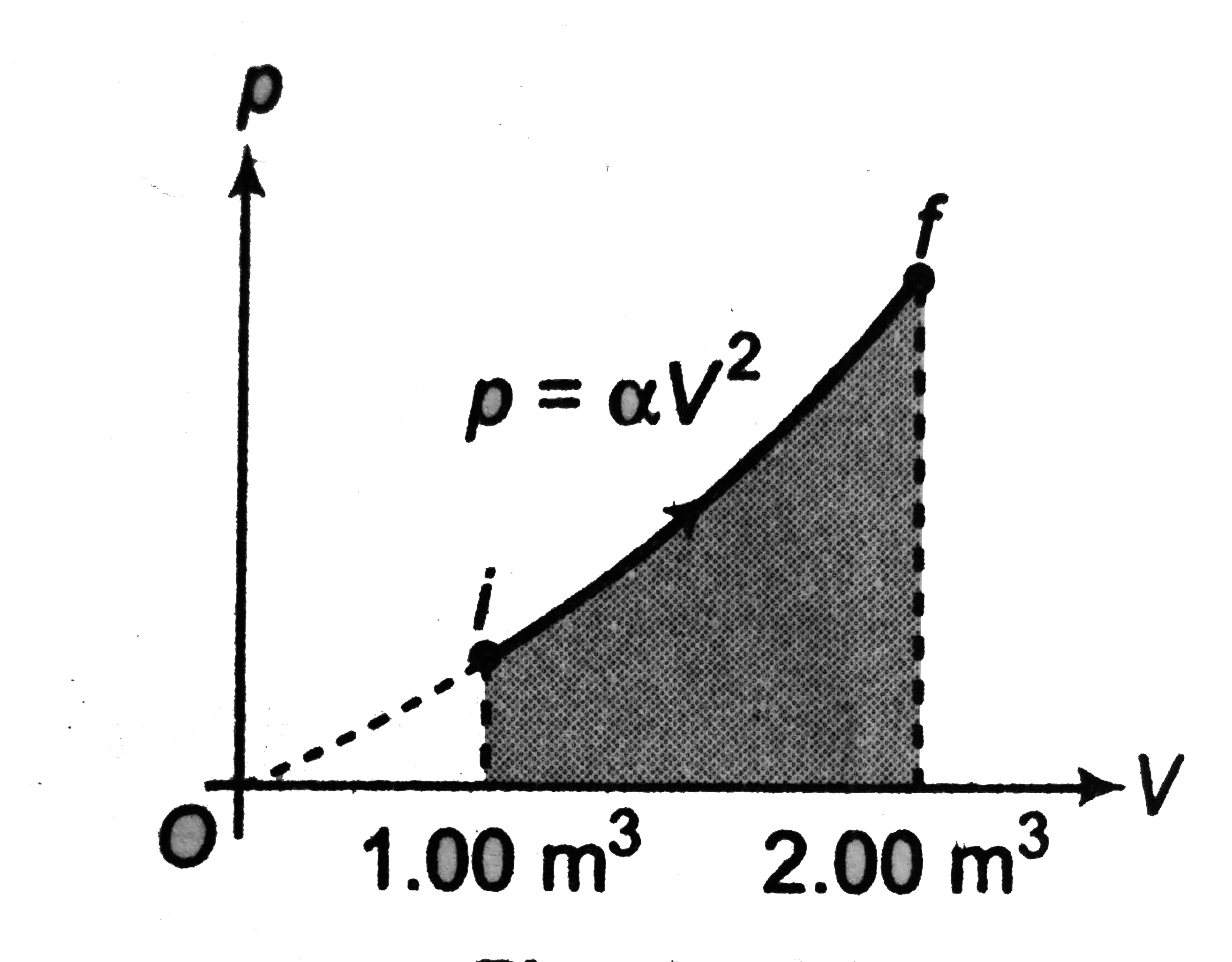
View SolutionA sample of ideal gas is expanded to twice its original volume of 1.00m3 in a quasi-static process for which p=αV2, with α=5.00atm/m6, as shown in Fig. How much work is done by the expanding gas?

View SolutionA gas can expand from 100mL to 250mL under a constant pressure of 2 atm. The work done by the gas is
View SolutionA sample of gas (γ=1.5) is taken through an adiabatic process in which the volume is compressed from 1600cm3→400cm3. If the initial pressure is 150kPa, (a) what is the final pressure and (b) how much work is done by the gas in the process?
View Solution5 mole of an ideal gas of volume is expanded against vaccum to make its volume 2 times, then work done by the gas is:
View SolutionA sample of gas expands from volume V1 to V2. The amount of work done by the gas is greatest when the expansion is
View Solution16kg oxygen gas expands at STP to occupy double of its oxygen volume. The work done during the process is:
View SolutionA diatomic gas done 80J work when expanded isobarically. Find the heat given to the gas during this process?
View SolutionA sample of an ideal gas is expanded 1m3 to 3m3 in a reversible process for which P=KV2 , with K=6bar/m6. What is work done by the gas (in kJ) ?
View SolutionOne mole of an ideal gas is expanded from a volume of 3L to 5L under a constant pressure of 1 atm. Calculate the work done by the gas.
View Solution
