An infinitely long rod lies along the axis of a concave mirror of focal length f. The near end of the rod is distance u>f from the mirror. Its image will have length
ufu−f
ufu+f
f2u+f
f2u−f
The correct Answer is:D
To solve the problem of finding the image length of an infinitely long rod placed along the axis of a concave mirror, we can follow these steps:
Step 1: Understand the Setup
We have a concave mirror with a focal length f and an infinitely long rod positioned such that the near end of the rod is at a distance u from the mirror, where u>f.
Step 2: Use the Mirror Formula
The mirror formula relates the object distance u, the image distance v, and the focal length f:
1v+1u=1f
Since we are dealing with a concave mirror, the object distance u will be taken as negative:
1v−1|u|=−1f
Thus, we can rearrange this to find v:
1v=1|u|−1f
Step 3: Solve for Image Distance v
Rearranging gives:
v=11|u|−1f=uff−u
Here, we have used the fact that |u|=u since u is given as positive and greater than f.
Step 4: Determine the Image Length
The image of the infinitely long rod will also be infinitely long, but we need to find the distance from the mirror to the image of the near end of the rod. The image length L′ can be calculated as:
L′=v−f
Substituting the expression for v:
L′=uff−u−f
To simplify this:
L′=uf−f(f−u)f−u=uf−f2+uff−u=2uf−f2f−u
Step 5: Final Image Length
Thus, the length of the image of the rod is given by:
L′=f2u−f
Conclusion
The image length of the infinitely long rod is:
f2u−f
We have a concave mirror with a focal length f and an infinitely long rod positioned such that the near end of the rod is at a distance u from the mirror, where u>f.
The mirror formula relates the object distance u, the image distance v, and the focal length f:
1v+1u=1f
Since we are dealing with a concave mirror, the object distance u will be taken as negative:
1v−1|u|=−1f
Thus, we can rearrange this to find v:
1v=1|u|−1f
Rearranging gives:
v=11|u|−1f=uff−u
Here, we have used the fact that |u|=u since u is given as positive and greater than f.
The image of the infinitely long rod will also be infinitely long, but we need to find the distance from the mirror to the image of the near end of the rod. The image length L′ can be calculated as:
L′=v−f
Substituting the expression for v:
L′=uff−u−f
To simplify this:
L′=uf−f(f−u)f−u=uf−f2+uff−u=2uf−f2f−u
Thus, the length of the image of the rod is given by:
L′=f2u−f
The image length of the infinitely long rod is:
f2u−f
Topper's Solved these Questions
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - B. More than one option is correct
20 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - C. comprehension type question
14 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
Similar Questions
For a concave mirror of focal length f, image is 2 times larger. Then the object distance from the mirror can be
View SolutionA short linear object of length b lies along the axis of a concave mirror or focal length f at a distance u from the pole of the mirror. The size of the image is approximately equal to
View SolutionOn the axis of a spherical mirror of focal length f a short linear object of length L lies on the axis at a distance μ from the mirror. Its image has an axial length L' equal to
View SolutionA luminous point object is moving along the principal axis of a concave mirror of focal length 12 cm towards it. When its distance from the mirror is 20 cm its velocity is 4 cm/s. the velocity of the image in cm/s at that instant is
View Solution(a) A short linear object of length b lies along the axis of a concave mirror of focal length f at a distance u from the pole. What is the size of the image? (b) If the object begins to move with speed V0 , what will be the speed of its image?
View SolutionA point object is moving on the principal axis of a concave mirror of focal length 24cm towards the mirror. When it is at a distance of 60cm from the mirror, its velocity is . 9sec/cm What is the velocity of the image at that instant
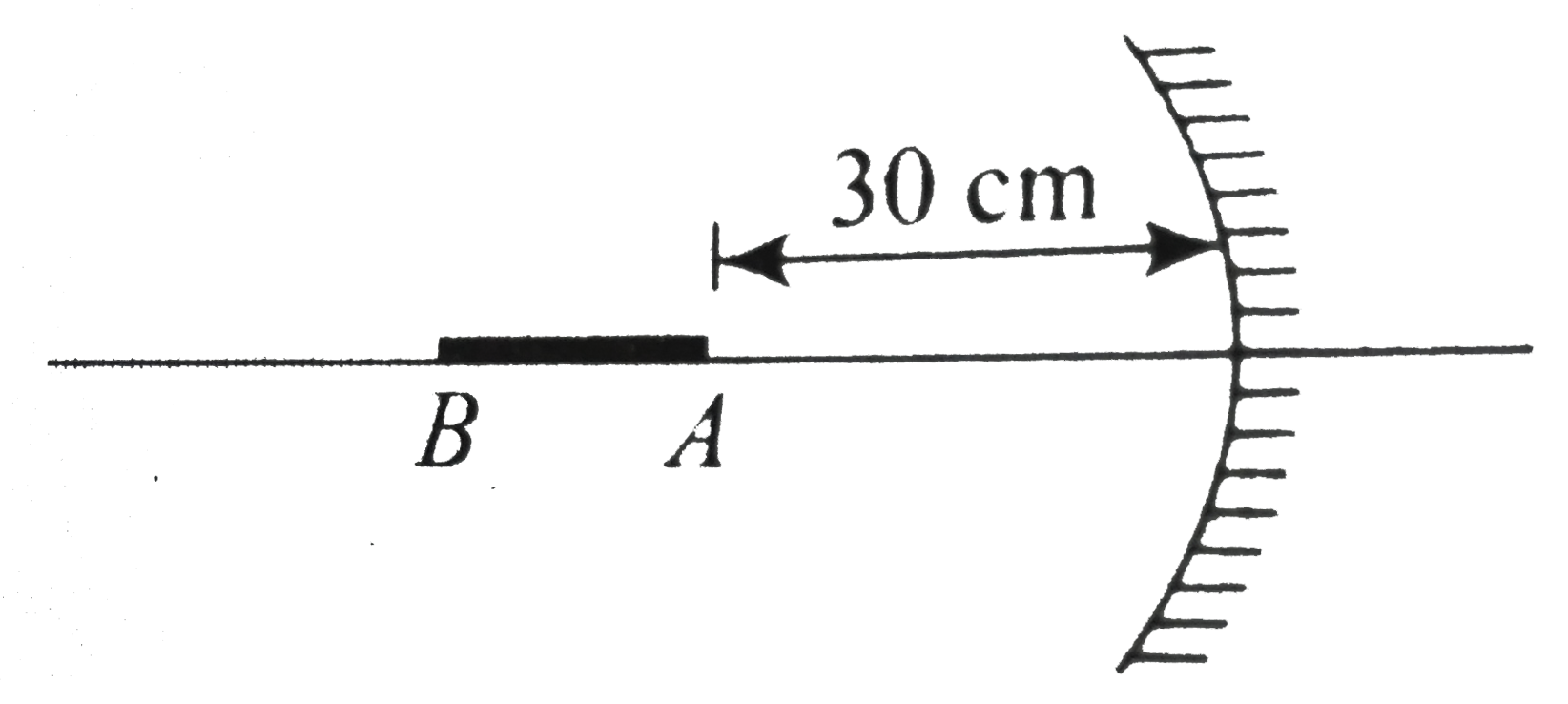
View SolutionObject AB is placed on the axis of a concave mirror of focal length 10cm. End A of the object is at 30cm from the mirror. Find the length of the image
a. if length of object is 5cm.
b. if length of object is 1 mm.
View SolutionAn object is placed at 20 cm from a convex mirror of focal length 20 cm. The distance of the image from the pole of the mirror is
View SolutionThe image formed by a convex mirror of focal length 30cm. is a quarter of the object. What is the distance of the object from the mirror ?
View SolutionA thin rod of length (f3) is lying along the principal axis of a concave
mirror of focal length f.Image is real , magnified and inverted and one of the end or rod coincides with its image itself. Find length of the image.
View Solution
