An iron ball hangs from a 21.5m steel cable and is used in the demolition of a building at a location where the acceleration due to gravity is 9.75m/s2. The ball is swung outward from its equilibrium position for a distance of 4.20m. Assuming the system behaves as a simple pendulum, find the maximum speed of the ball during its swing.
4.45m/s
2.83m/s
17.8m/s
1.71 m/s
The correct Answer is:B
To find the maximum speed of the iron ball during its swing, we can use the principle of conservation of mechanical energy. Here are the steps to solve the problem:
1. Identify the parameters:
- Length of the steel cable (L) = 21.5 m
- Horizontal displacement (d) = 4.2 m
- Acceleration due to gravity (g) = 9.75 m/s²
2. Determine the height (h) raised:
- The height (h) to which the ball is raised can be calculated using the Pythagorean theorem. The vertical distance (x) from the pivot to the ball when swung out can be found as follows:
x=√L2−d2
Substituting the values:
x=√(21.5)2−(4.2)2=√462.25−17.64=√444.61≈21.1 m
- Now, calculate the height (h) raised:
h=L−x=21.5−21.1=0.4 m
3. Apply the conservation of energy:
- At the highest point of the swing, all the energy is potential energy (PE), and at the lowest point (equilibrium position), all the energy is kinetic energy (KE).
- Potential energy at the height (h):
PE=mgh
- Kinetic energy at the lowest point:
KE=12mv2
- By conservation of energy, we set PE equal to KE:
mgh=12mv2
- The mass (m) cancels out:
gh=12v2
4. Solve for maximum speed (v):
- Rearranging the equation gives:
v2=2gh
- Taking the square root:
v=√2gh
- Substituting the values:
v=√2×9.75×0.4=√7.8≈2.8 m/s
5. Conclusion:
- The maximum speed of the ball during its swing is approximately 2.83 m/s.
- Length of the steel cable (L) = 21.5 m
- Horizontal displacement (d) = 4.2 m
- Acceleration due to gravity (g) = 9.75 m/s²
- The height (h) to which the ball is raised can be calculated using the Pythagorean theorem. The vertical distance (x) from the pivot to the ball when swung out can be found as follows:
x=√L2−d2
Substituting the values:
x=√(21.5)2−(4.2)2=√462.25−17.64=√444.61≈21.1 m
- Now, calculate the height (h) raised:
h=L−x=21.5−21.1=0.4 m
- At the highest point of the swing, all the energy is potential energy (PE), and at the lowest point (equilibrium position), all the energy is kinetic energy (KE).
- Potential energy at the height (h):
PE=mgh
- Kinetic energy at the lowest point:
KE=12mv2
- By conservation of energy, we set PE equal to KE:
mgh=12mv2
- The mass (m) cancels out:
gh=12v2
- Rearranging the equation gives:
v2=2gh
- Taking the square root:
v=√2gh
- Substituting the values:
v=√2×9.75×0.4=√7.8≈2.8 m/s
- The maximum speed of the ball during its swing is approximately 2.83 m/s.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Problems39videos
OSCILLATIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)10videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - PHOTONS AND MATTER WAVESEXERCISE - PRACTICE QUESTIONS(Integer Type)4videos
PHOTONS AND MATTER WAVES
Similar Questions
A rubber ball is dropped from a height of 5m on a plane, where the acceleration due to gravity is not shown. On bouncing it rises to 1.8m. The ball loses its velocity on bouncing by a factor of
View SolutionA car is moving along a horizontal curve of radius 20 m , and coefficient of friction between the road and wheels of the car is 0.25 . If acceleration due to gravity is (9.8m/s2), then its maximum speed is
View Solution
Knowledge Check
- Question 1 - Select One
A ball is thrown upwards . Its height varies with time as shown in figure. If the acceleration due to gravity is 7.5m/s2, then the height h is
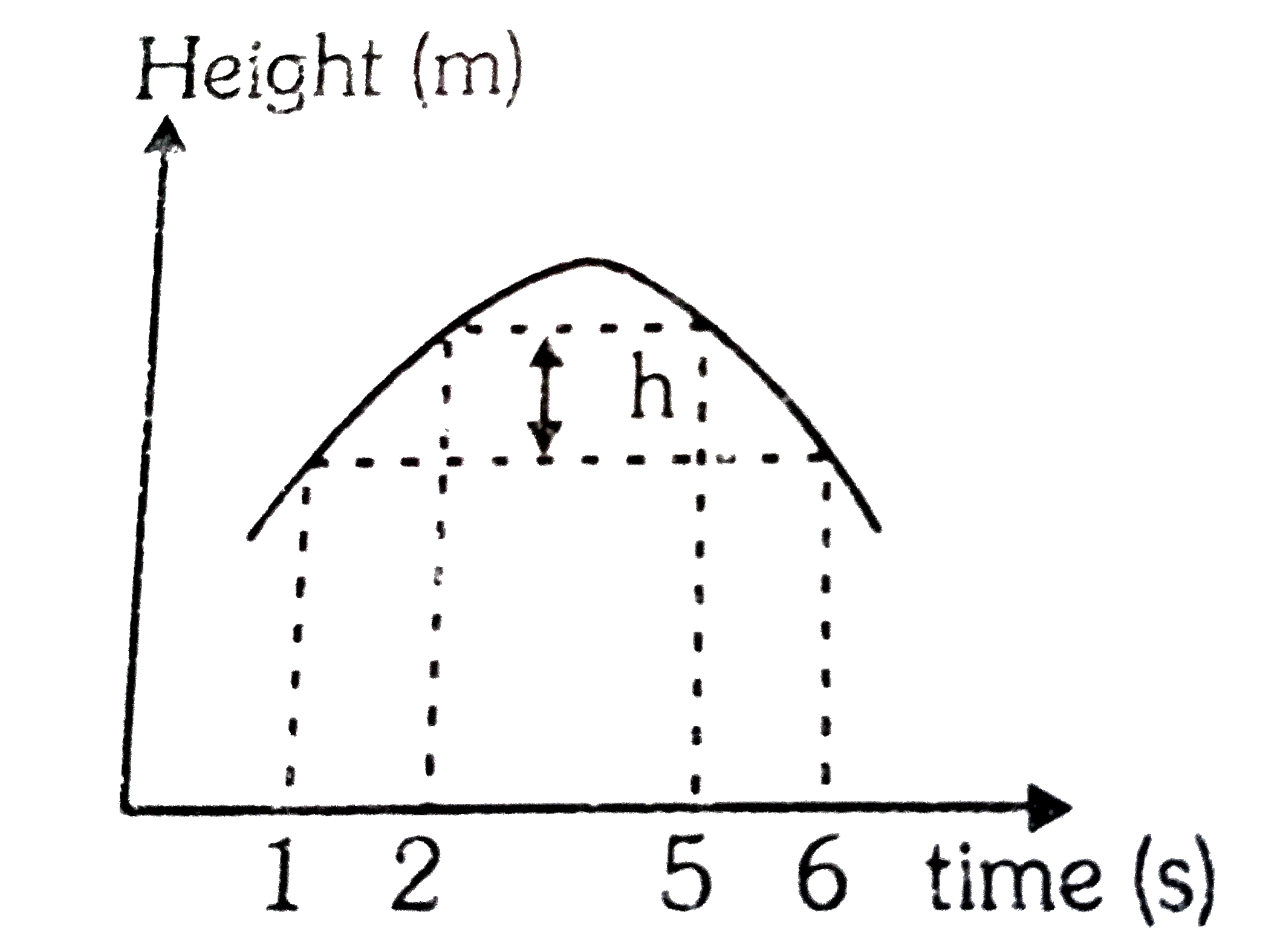 A10mB15mC20mD25m
A10mB15mC20mD25m - Question 2 - Select One
The acceleration due to gravity changes from 9.8m/s2 to 9.5m/s2. To keep the period of pendulum constant, its length must changes by
A3 mB0.3 mC0.003 mD3 cm - Question 3 - Select One
Two balls are dropped from the same point after an interval of 1s. If acceleration due to gravity is 10m/s2, what will be their separation 3 seconds after the release of first ball?
A5 mB10 mC25 mD30 m
Two simple pendulum A and B of lengths 1.69m and 1.44m start swinging at the time from a location where acceleration due to gravity is 10ms−1. Answer the following question.
After how much time, the two pendulums will be in phase again ?View SolutionTwo simple pendulum A and B of lengths 1.69m and 1.44m start swinging at the time from a location where acceleration due to gravity is 10ms−1. Answer the following question.
What will be the apporximate gain or loss ot time by pendulum A in a day with respect to second's pendulum ?View SolutionA simple pendulum consists of a ball of mass m suspended from the ceiling using a string of length L. The ball is displaced from its equilibrium position by a small angle θ. What is the magnitude of the restoring force that moves the toward its equilibrium position and produces simple harmonic motion?
View SolutionTwo simple pendulum A and B of lengths 1.69m and 1.44m start swinging at the time from a location where acceleration due to gravity is 10ms−1. Answer the following question.
How many vibratinos pendulum A will compelte when it will be out of phase with B ?View SolutionA ball falls from 20 m height on floor and rebounds to 5 m. Time of contact is 0.02 s. Find acceleration during impact.
View Solution

