An LR circuit with emf ε is connected at t = 0. (a) find the charge Q which flows through the battery during O to t. (b) Calculate the work done by the battery during this period. (d) find the magnetic field energy stored in the circuit at time t. (e) Verify that the results in the three parts above are consistent with energy conservation.
(a)(dq)=
=i0(1−e−t/(τ))dt
=i0(1−e−t/(τ))dt[∴(τ)=(LR)]
Q=int_(0)^(t) (dq)<br>=i_(0)[int_(0)^(t)(dt)-int_(0)^(t)(e^(-(tR)//L)(dt)]<br>i_(0)[t-(L/R)(1-(e^(-(tR)//L))]<br>i_(0)[t-(-(L)/(R))(1-(e^(-(tR)//L))]_(0)^(t)<br>Q=(E/R)[t-((L)/(R))(1-(e^(-(tR)//L))]<br>(b)similarlyasweknowworkdo≠<br>=Vl=Ei
Ei0[t−(LR)(1−(e−(tR)/L))]
=E2R[t−(LR)(1−(e−(tR)/L)]
(c) H=∫t0(i2)(R).(dt)
=E2R2.R.∫t0(1−(e−(tR)/L)2.(dt)
E2R∫t0(1−(e−(2tR)/L)−2e−(tR)/L)(dt)]
E2R(t−L2Re−2tR/L+LR2.(e−(tR)/L))t0
E2R(t−L2Re−2tR/L+LR2.(e−(tR)/L))
−(−L2R+2LR)
E2R{t−L2R(x2−4x+3)}
[wherex=e−tR/L]
(d) E=(12)Li2=12(L)(E2R2(1−(e−(tR)/L))2
(LE)22R2(1−x)2
[wherex=(e−(tR)/L)]
(e) Total energy stored in magnetic field
E2Rt−E2LR2(e−(tR)/L)
E2R{t−L2R(1−x)}
=Energy drawn from battery.
(Hence conservation of energy hold good).
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE9videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 210videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises75videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercises9videos
ELECTROMAGNETIC WAVES
Similar Questions
A capacitor having a capacitance of 200 μF is charged to a potential difference of 20V. The charging battery is disconnected and the capacitor is connected to another battery of emf 10V with the positive plate of the capacitor joined with the positive terminal of the battery.
(a) Find the charges on the capacitor before and after the reconnection in steady state.
(b) Find the net charge flown through the 10 V battery
Is work done by the battery or is it done on the battery? Find its magnitude.
(d) Find the decrease in electrostatic field energy.
(e) Find the heat developed during the flow of charge after reconnection .View SolutionA parellel - plate capacitor having plate area 20cm2 and seperation between the plates 1.00mm is connected to a bettery of 12.0V. The plates are pulled apart to incrase the separation to 2.0mm . (a ) calculate the charge flown through the circuit during the process . (b ) How much energy is absorbed by the bettery during the process ? (c ) calculate the stored energy in the electric field before and after the process . (d ) Using the expression for the force between the plates , find the work done by the person polling the plates apart . (e ) Show and justify that no heat is producted during this transfer of charge as the separation is increased.
View Solution
Knowledge Check
- Question 1 - Select One
In the circuit shown in figure switch S is closed at time t=0. The charge which passes through the battery in one time constant is
 AeR2ELBE(LR)CELeR2DeLER
AeR2ELBE(LR)CELeR2DeLER - Question 2 - Select One
The heat produced by a resistor in any time t during the charging of a capacitor in a series circuit is half the energy stored in the capacitor by that time.
Current in the circuit is equal to the rate of increase in charge on the capacitor.ABoth A and R falseBBoth A and R true and R is not correct reason for ACA is true and R is falseDBoth A and R are true and R is correct reason of A. - Question 3 - Select One
If maximum energy is stored in capacitor at t = 0 then find the time after which current in the circuit will be maximum.
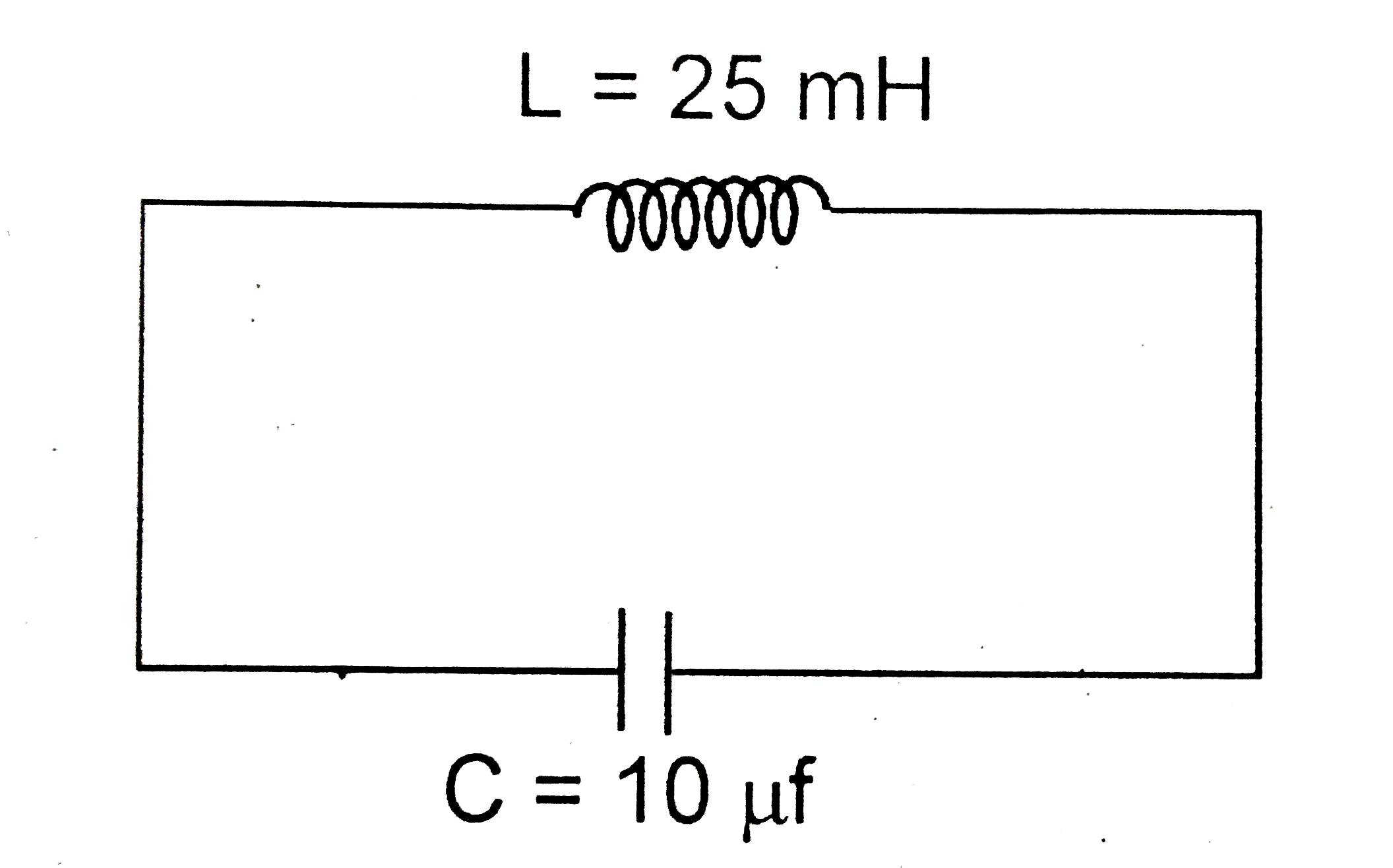 Aπ2msBπ4msCπmsD2ms
Aπ2msBπ4msCπmsD2ms
A coil having an inductance L and a resistance R is connected to a battery of emf E . Find the time taken for the magnetic energy stored in the circuit to change from one fourth of the steady-state value.
View SolutionIn the circuit shown all the resistors are of same resistance R=11Ω and C=2μF. They are connected through a battery of 10 V. When the cell is switched on, find
(a) maximum current in the circuit, and
(b) energy stored in the capacitor after time t
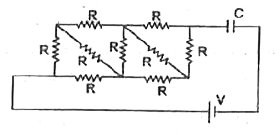 View Solution
View SolutionA coil of inductance 1H and resistance 10Ω is connected to a resistanceless battery of emf 50V at time t=0. Calculate the ratio of rthe rate which magnetic energy is stored in the coil to the rate at which energy is supplied by the battery at t=0.1s.
View SolutionAt t=0 , switch S closed. Find the ratio of the rate at which magnetic energy stored in the coil to the rate at which energy is supplied by the battery at time t=τ=L/R .
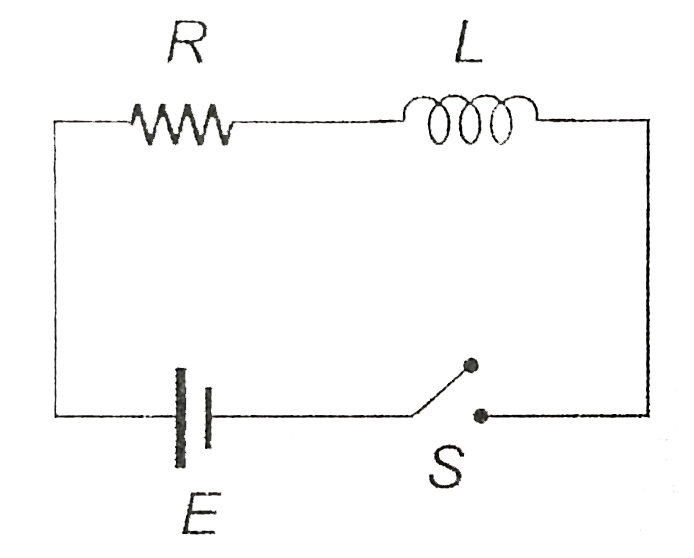 View Solution
View SolutionA circuit contains an inductor of value 2H as shown at t=0 no current was flowing through battery. Find the energy stored in inductor at t=4 sec.
 View Solution
View Solution

