Question

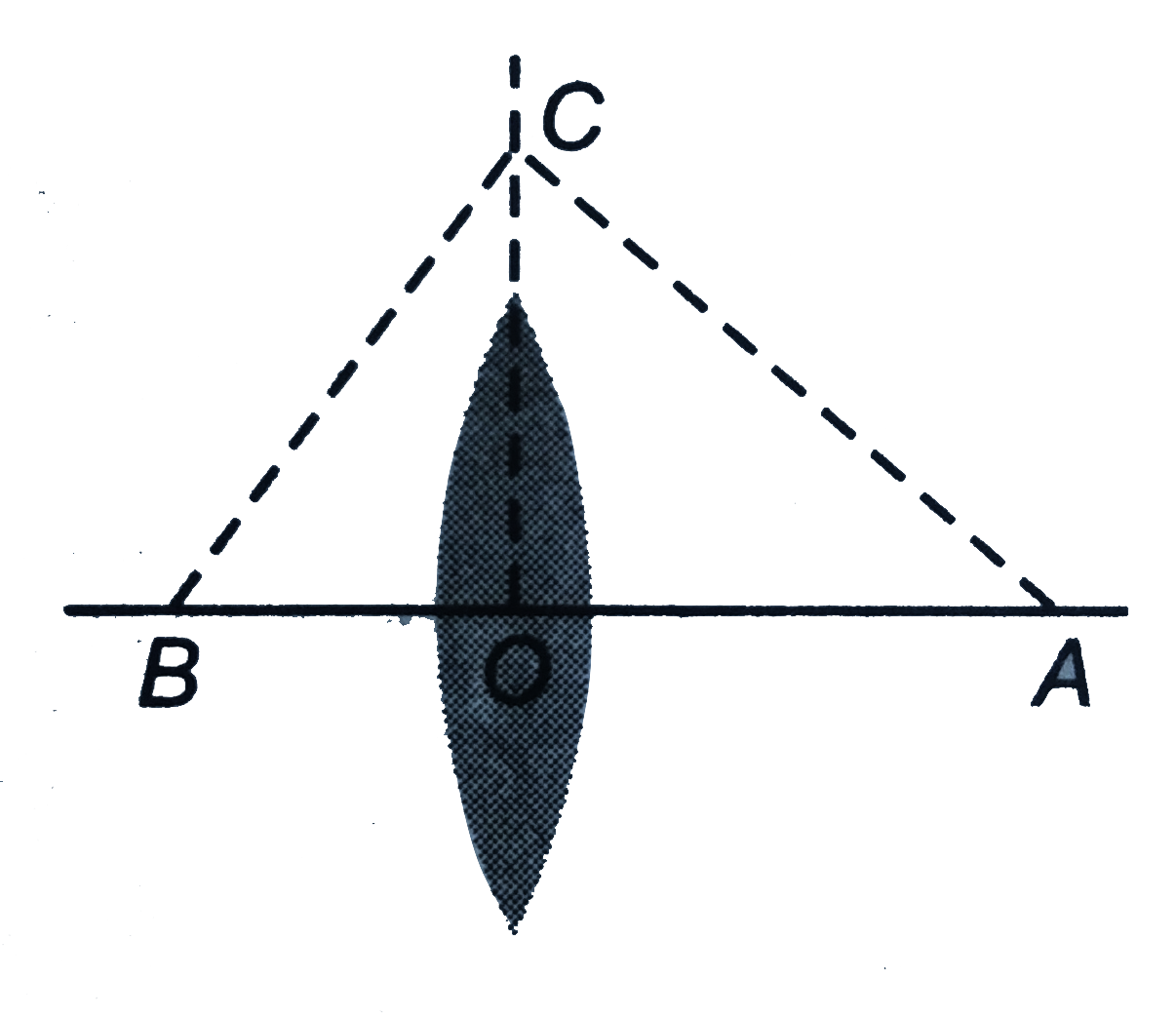
An object is placed at $A(OA>f)$. Here, f is the focal length of the lens. The image is formed at B. A perpendicular is erected at O and C is chosen such that $\angle BCA={90}^{\circ }$. Let OA = a, OB = b and OC = c. Then the value of f is

Options

A. `((a+b)^(3))/(c^(2))`
B. `((a+b)c)/((a+c))`
C. `(c^(2))/(a+b)`
D. `(a^(2))/(a+b+c)`

Answer

C

Explanation

To solve the problem step by step, we will follow the concepts of lens optics and the Pythagorean theorem.

Step 1: Understanding the Setup
We have an object placed at point A, and the distance from the optical center O to A is denoted as OA = a. The image is formed at point B, with OB = b. A perpendicular is erected at O, and point C is chosen such that angle BCA = 90°.

Step 2: Use the Lens Formula
The lens formula is given by:
\( \frac{1}{v} - \frac{1}{u} = \frac{1}{f} \)
where:
- \( v \) is the image distance (OB = b)
- \( u \) is the object distance (OA = -a, as per the sign convention for lenses)
- \( f \) is the focal length of the lens.

Since OA is greater than f, we can write:
\( \frac{1}{b} + \frac{1}{a} = \frac{1}{f} \)
This simplifies to:
\( \frac{a + b}{ab} = \frac{1}{f} \)
Thus, we can express \( f \) as:
\( f = \frac{ab}{a + b} \)

Step 3: Apply the Pythagorean Theorem
In triangle ABC, since angle BCA = 90°, we can apply the Pythagorean theorem:
\( AB^2 = AC^2 + BC^2 \)
Here, \( AB \) is the hypotenuse, which is the distance from A to B, and can be expressed as:
\( AB = OA + OB = a + b \)
Let \( OC = c \). Therefore, we have:
\( (a + b)^2 = c^2 + b^2 \)

Step 4: Expand and Rearrange
Expanding the left side:
\( a^2 + 2ab + b^2 = c^2 + b^2 \)
Now, we can cancel \( b^2 \) from both sides:
\( a^2 + 2ab = c^2 \)
This can be rearranged to:
\( c^2 = a^2 + 2ab \)

Step 5: Relate c to f
From the previous step, we can express \( f \) in terms of \( c \):
\( f = \frac{c^2}{a + b} \)

Step 6: Substitute for c^2
We already found that:
\( c^2 = a^2 + 2ab \)
Substituting this into the expression for \( f \):
\( f = \frac{a^2 + 2ab}{a + b} \)

Step 7: Final Simplification
Now, we can simplify this expression:
\( f = \frac{a^2 + 2ab}{a + b} = \frac{a(a + 2b)}{a + b} \)
This gives us the final expression for the focal length \( f \).

Conclusion
Thus, the value of \( f \) is:
\( f = \frac{c^2}{a + b} \)