An object of mass 4 kg is attached to a spring having spring constant 100Nm. It performs simple harmonic motion on a smooth horizontal surface with an amplitude of 2 m. A 6 kg object is dropped vertically onto the 4 kg object when it crosses the mean position, and sticks to it. the change in amplitude of oscillation due to collision is
1m
zero
2[1−√25]
2[1−1√5]
The correct Answer is:C
Time period of the system (object of mass 4 kg) before collision is T1=2π√4100
After collision, time period of the combined mass is
T2=2π√10100
We can apply momentum conservation for just before the collision and just after the collision in the horizontal direction.
4A1ω1=10A2ω2⇒A4×2×√100410×√10010=2√25m
So change in amplitude, △A=A1−A2=2[1−√25]m
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning
6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective
21 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
A block of mass 4kg attached with spring of spring constant 100N/m is executing SHM of amplitude 0.1m on smooth horizontal surface as shown in figure. If another block of mass 5kg is gently placed on it, at the instant it passes through the mean position and new amplitude of motion is n−1 meter then find n. Assuming that two blocks always mvoe together .
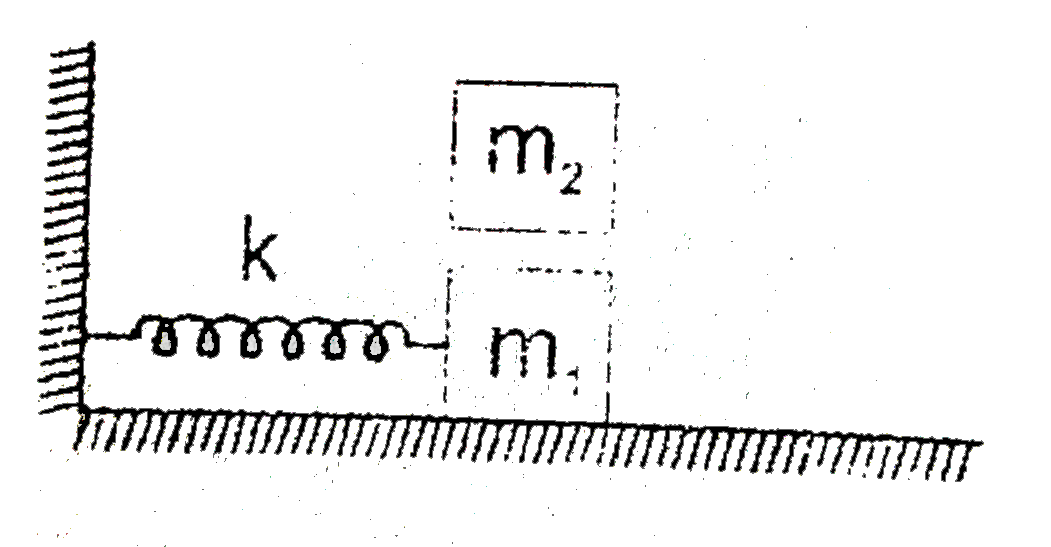
View SolutionAn object of mass m, oscillating on the end of a spring with spring constant k has amplitude A. its maximum speed is
View Solution
Knowledge Check
A 0.20kg object mass attached to a spring whose spring constant is 500N/m executes simple harmonic motion. If its maximum speed is 5.0m/s, the amplitude of its oscillation is
A0.0020mB0.10mC0.20mD25mA particle of mass 3 kg , attached to a spring with force constant 48Nm−1execute simple harmonic motion on a frictionless horizontal surface. The time period of oscillation of the particle, is seconds , is
Aπ4Bπ2C2πD8πA mass m, which is attached to a spring with spring constant k, oscillates on a horizontal table, with amplitude A. At an instant when the spring is streched by √3A/2, a second mass m is dropped vertically onto the original mass and immediately sticks to it. what is the amplitude of the resulting motion-
A√32AB√78AC√1316AD√23A
A body of mass of 4 kg is mounted on four vertical springs each having a spring constant of 400 N/m. The period with which the body vibrates vertically is
View Solution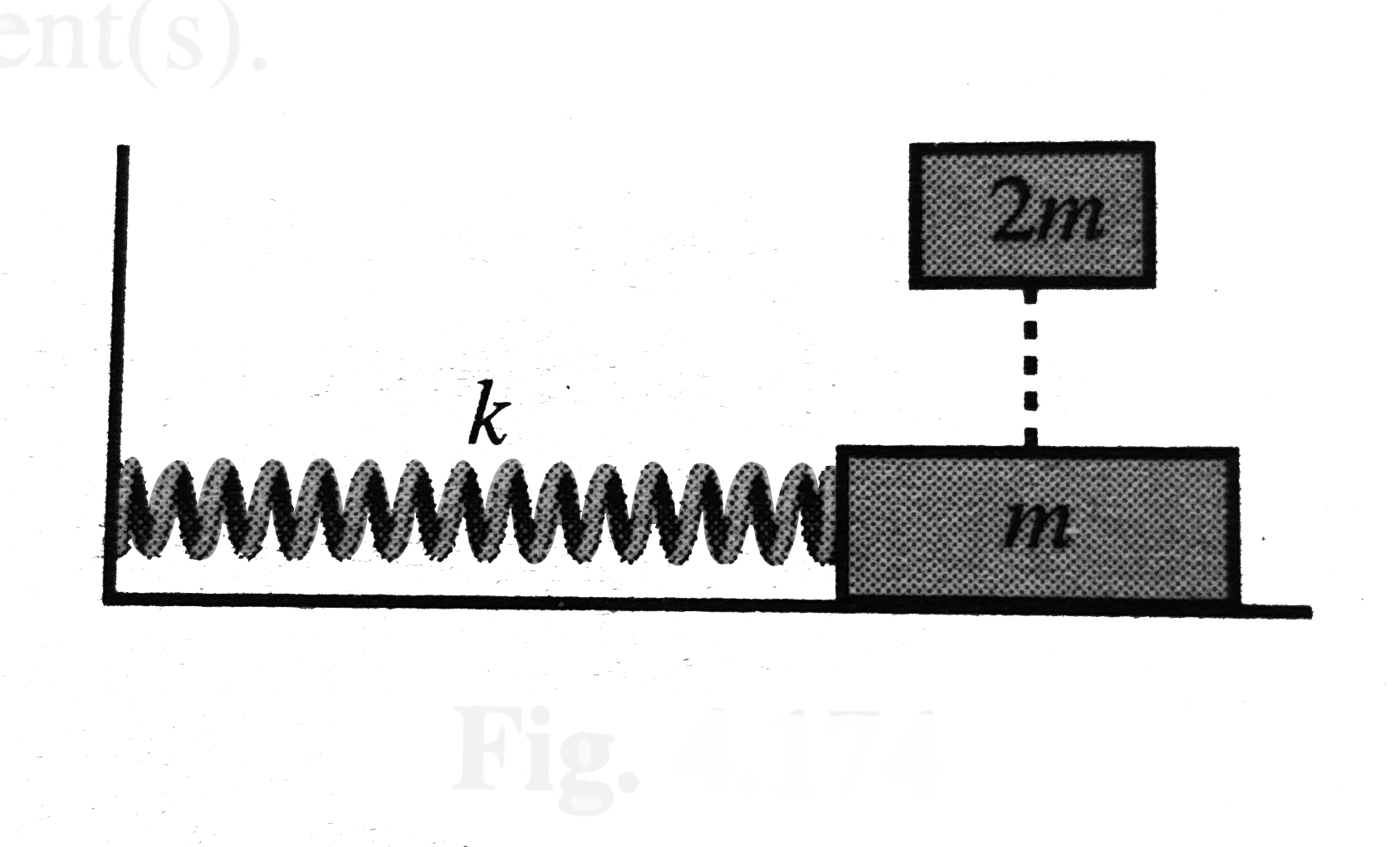
An object of mass m is performing simple harmonic motion on a smooth horizontal surface as shown in Fig. just as the oscillating object reaches its extreme position, another object of mass 2 m is dropped on to oscillating object, which sticks to it. For this situation mark out the correct statement (s).
View SolutionAn object of mass m is performing simple harmonic motion on a smooth horizontal surface as shown in figure. Just as the oscillating object reaches its extreme position, another object of mass 2m is dropped on it, which sticks to it. For this situation, mark out the correct statement(s).
View SolutionA body of mass 0.25 kg is attached to a vertical spring. The spring is executing damped simple harmonic spring will drop to half its initial value ? [The damping constant b = 0.05 kg/s]
View SolutionA 1 kg mass is attached to a spring of force constant 600 N/m and rests on a smooth horizontal surface with other end of the spring tied to wall as shown in figure. A second mass of 0.5 kg slides along the surface towards the first at 3m/s. If the masses make a perfectly inelastic collision, then find amplitude and time period of oscillation of combined mass.

View Solution
