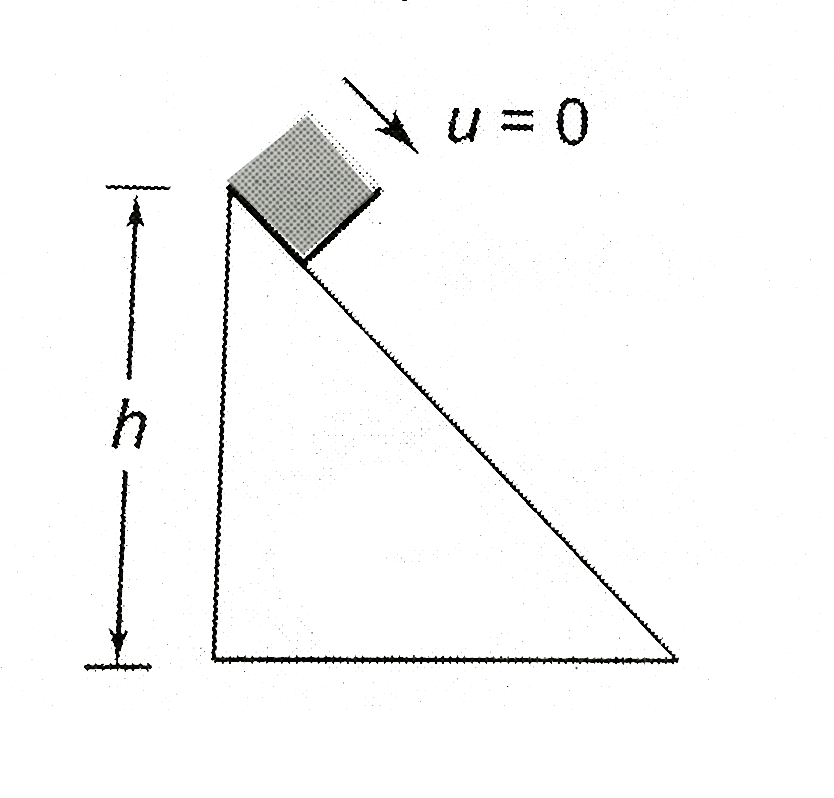An object of mass m is allowed to fall from rest along a rough inclined plane. The speed of the object on reaching the bottom of the plane is proportional to:
m0
m
m2
m−1
From work work energy principal.
12mv2=mgh−μmgcosθhsinθ
v−√2gh−2μmgcosθ or v∝m0.
Topper's Solved these Questions
Similar Questions
Knowledge Check
An object of mass m is released from rest from the top of a smooth inclined plane of height h. Its speed at the bottom of the plane is proportional to
Am0BmCm2Dm−1A block of mass m is released from the top of a mooth inclined plane of height h its speed at the bottom of the plane is proportion to
Am0BmCm2Dm−1A disc of mass 3 kg rolls down an inclined plane of height 5 m. The translational kinetic energy of the disc on reaching the bottom of the inclined plane is
A50 JB100 JC150 JD175 J
A block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionA small blockofmass 'm' is released from rest at the top of a rough inclined plane as shown The coefficient of friction between the block and inclined plane is 'μ' Using work-energy theorem, find the speed of block as it passes the lowest point.
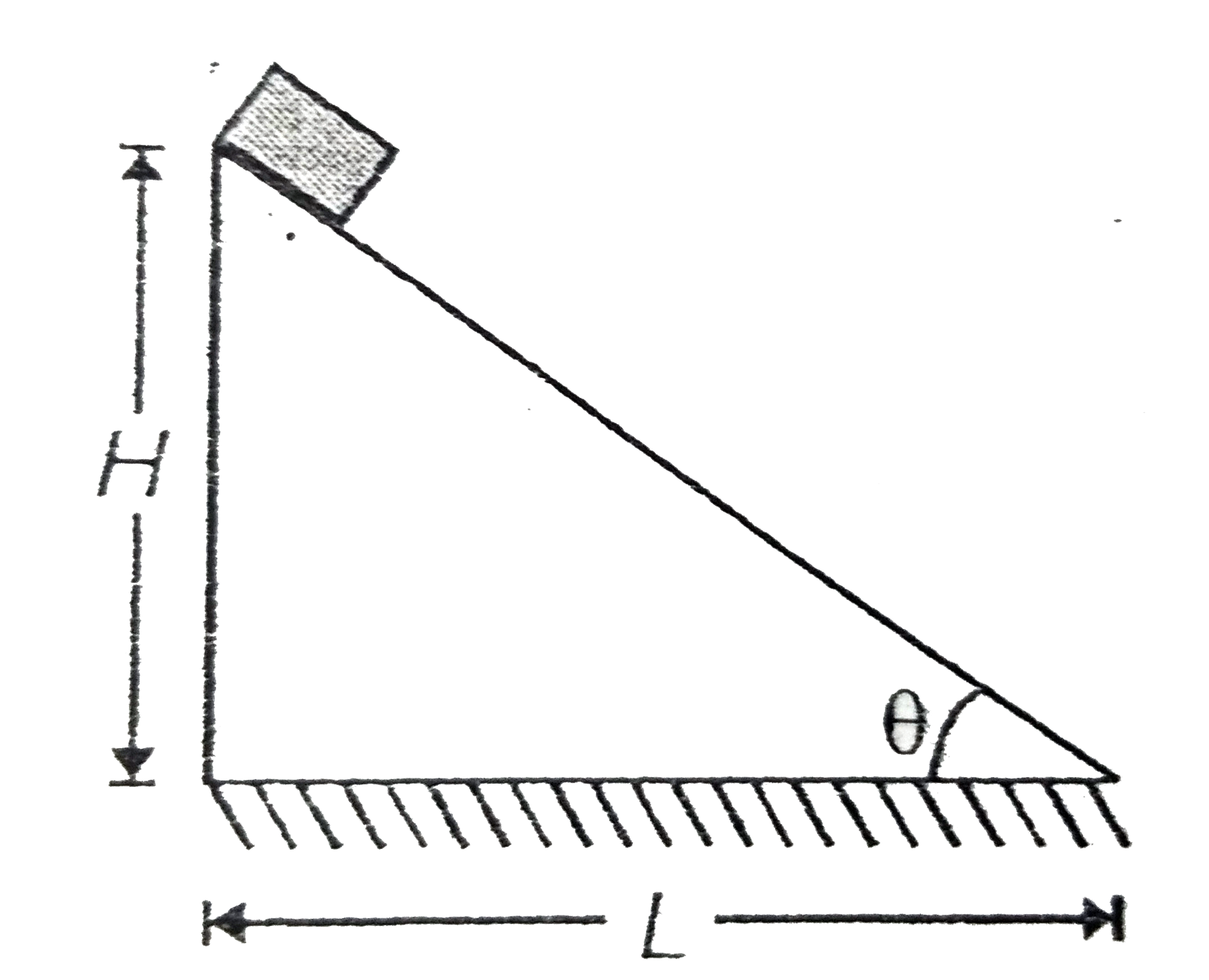
View SolutionA block of mass 4kg is released from the top of a rough inclines plane of height 10m. If velocity of the block is10ms at the bottom of the inclined then work done by the friction force on the block will be
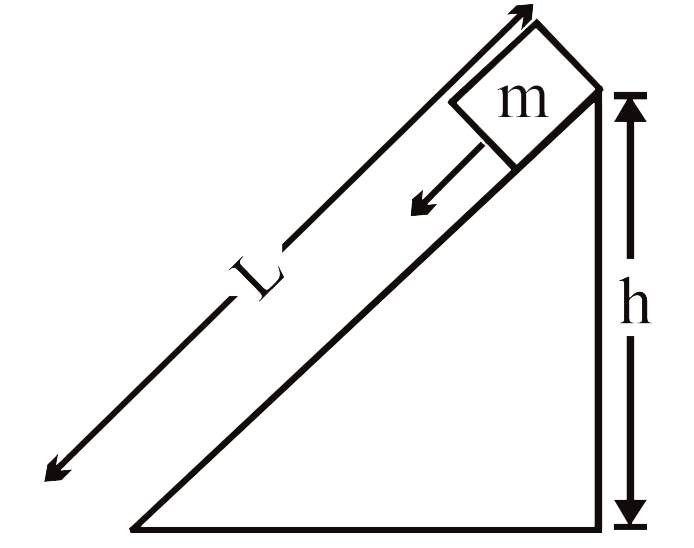
View SolutionA body of mass m is released from the top of a rough inclined plane as shown in figure. If the frictional force be F, then body will reach the bottom with a velocity
View SolutionThere different objective of masses m1,m2 and m2 are allowed to fall from rest and from the same point O along three difference frictionless path .The speeds of three objects on reaching the ground will be
View Solution