An open cubical tank was initially fully filled with water. When the tank was accelerated on a horizontal plane along one of its side it was found that one thrid of volume of water was spilled out. The acceleration was
g/3
2g/3
g/2
g/4
The correct Answer is:B
To solve the problem step by step, we will analyze the situation of the cubical tank filled with water and how the acceleration affects the water level.
Step 1: Understand the initial conditions
The tank is a cube with side length L. The initial volume of water in the tank is:
V=L3
Step 2: Analyze the effect of acceleration
When the tank is accelerated horizontally, the water inside will tilt, creating an angle θ with respect to the horizontal. One-third of the volume of water spills out, which means that two-thirds of the volume remains in the tank.
Step 3: Calculate the remaining volume of water
Since one-third of the volume spills out, the remaining volume V′ is:
V′=V−V3=2V3=2L33
Step 4: Determine the geometry of the water
When the tank is tilted, the water forms a triangular prism shape on one side. The height of the water on the side where it is lower can be represented as L−x, where x is the horizontal distance from the bottom of the tank to the new water level.
Step 5: Calculate the volume of the remaining water
The volume of the remaining water can be expressed as the sum of the volume of the triangular part and the rectangular part:
1. The triangular part has a base of L and height L−x:
Volume of triangular part=12×base×height×width=12×L×(L−x)×L=L2(L−x)2
2. The rectangular part has a height x:
Volume of rectangular part=L×x×L=L2x
Combining these volumes gives:
V′=L2(L−x)2+L2x=L2(L−x+2x)2=L2(L+x)2
Step 6: Set up the equation for volume
We know that the remaining volume V′ is equal to 2L33:
L2(L+x)2=2L33
Step 7: Solve for x
Cross-multiplying gives:
3L2(L+x)=4L3
Dividing by L2 (assuming L≠0):
3(L+x)=4L
3x=4L−3L=L
x=L3
Step 8: Relate x to the angle θ
Using the triangle formed by the water level, we have:
tanθ=L−xL=L−L3L=2L3L=23
Step 9: Use the relationship between acceleration and angle
From the relationship tanθ=Ag:
Ag=23
Thus, the acceleration A is:
A=2g3
Final Answer
The acceleration of the tank is:
2g3
The tank is a cube with side length L. The initial volume of water in the tank is:
V=L3
When the tank is accelerated horizontally, the water inside will tilt, creating an angle θ with respect to the horizontal. One-third of the volume of water spills out, which means that two-thirds of the volume remains in the tank.
Since one-third of the volume spills out, the remaining volume V′ is:
V′=V−V3=2V3=2L33
When the tank is tilted, the water forms a triangular prism shape on one side. The height of the water on the side where it is lower can be represented as L−x, where x is the horizontal distance from the bottom of the tank to the new water level.
The volume of the remaining water can be expressed as the sum of the volume of the triangular part and the rectangular part:
1. The triangular part has a base of L and height L−x:
Volume of triangular part=12×base×height×width=12×L×(L−x)×L=L2(L−x)2
2. The rectangular part has a height x:
Volume of rectangular part=L×x×L=L2x
V′=L2(L−x)2+L2x=L2(L−x+2x)2=L2(L+x)2
We know that the remaining volume V′ is equal to 2L33:
L2(L+x)2=2L33
Cross-multiplying gives:
3L2(L+x)=4L3
Dividing by L2 (assuming L≠0):
3(L+x)=4L
3x=4L−3L=L
x=L3
Using the triangle formed by the water level, we have:
tanθ=L−xL=L−L3L=2L3L=23
From the relationship tanθ=Ag:
Ag=23
Thus, the acceleration A is:
A=2g3
The acceleration of the tank is:
2g3
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - DC PANDEYCHAPTER - PROPERTIES OF MATTEREXERCISE - More than one option is correct
21 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEYCHAPTER - PROPERTIES OF MATTEREXERCISE - Comprehension
32 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEYCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
- PROJECTILE MOTIONBOOK - DC PANDEYCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
- RAY OPTICSBOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - Integer type q.
15 Videos
Similar Questions
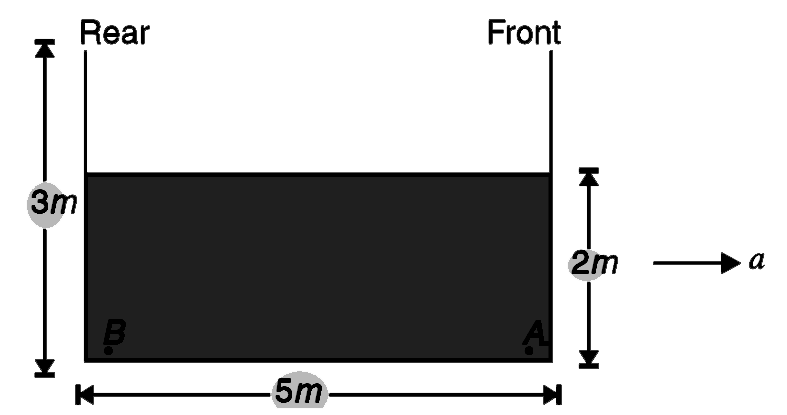
An open rectangular tank 5mxx4mxx3m in dimension is containing water up to a height of 2m the tank is accelerated horizontally along the longer side. Assuming water to be and ideal liquid find-
(a) the maximum acceleration with which the tank can be moved so that water does not fall from the rear side.
(b) the gauge pressure at the bottom of the front and back of the tank (points A and B) if the tank is closed at the top and is then acclerated horizontally at 9m/s2. Assume that the top cover has a small hole at the right side of the tank so taht pressure of air inside the tank is maintained at atmospheric pressure. Gauge pressure at a point is difference in absolute pressure at the point and atmospheric pressure.
View SolutionAn open cubical tank completely filled with water is kept on a horizontal surface. Its acceleration is then slowly increasesd to 2m/s2 as shown in the figure. The side of the tank is 1m. Find the mass of water that would spill out of the tank.

View Solution
Knowledge Check
A closed cubical box is completely filled with water and is accelerated horizontally towards right with an acceleration a. The resultant normal force by the water on the top of the box.
Apasses through the centre of topBpasses through a point to the righ of the centreCpasses through a point to the left of the centreDbecomes zeroA closed rectangular tank is completely filled with water and is accelerated horizontally with an acceleration towards the righ. Pressure is i. maximum and ii. minimum at
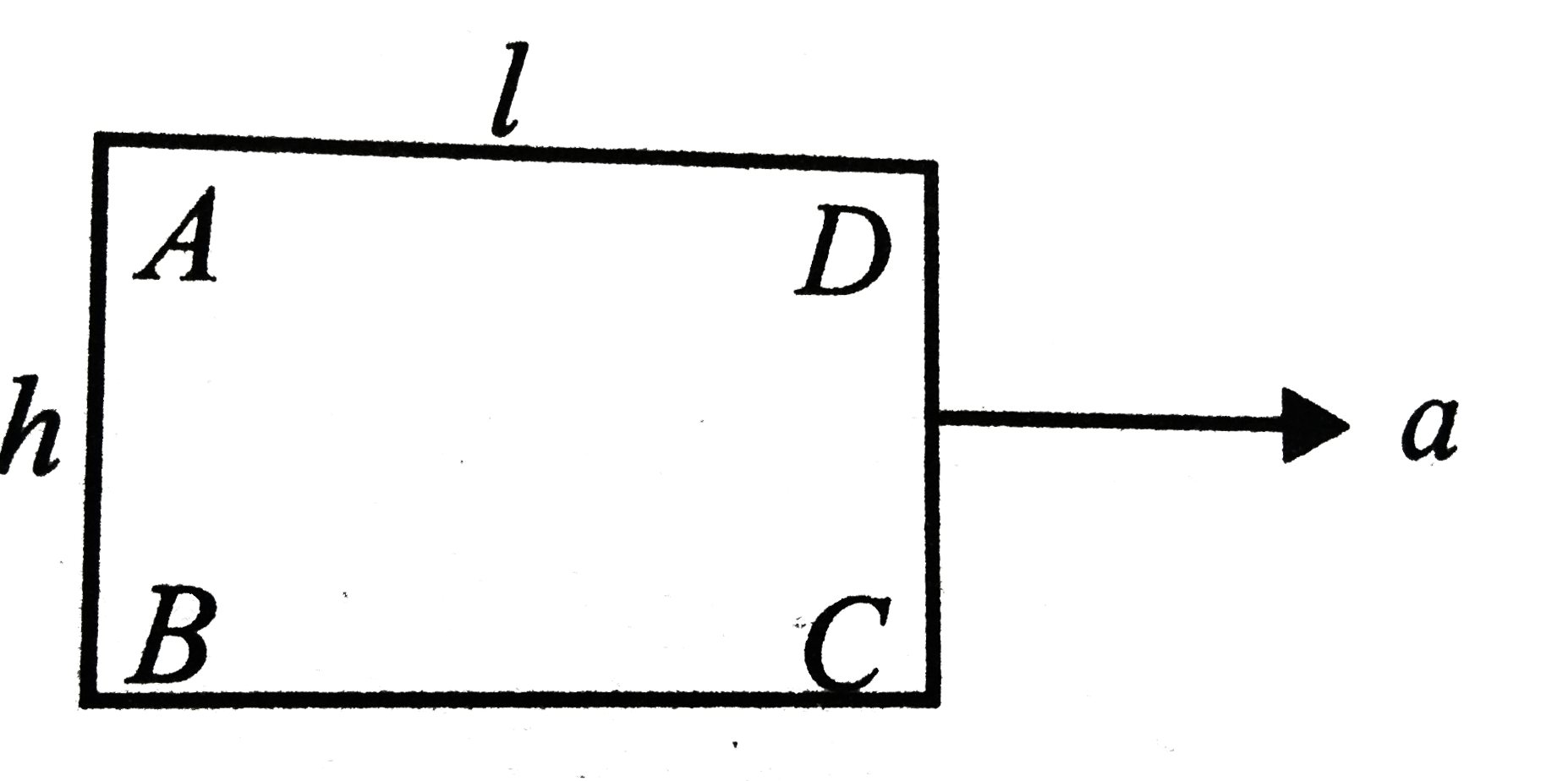 Ai. B ii DBi C ii DCi B ii CDi B ii A
Ai. B ii DBi C ii DCi B ii CDi B ii AA tank if filled with water upto height H. When a hole is made at a distance h below the level of water. What will be the horizontal range of water jet ?
A2√h(H−h)B4√h(H+h)C4√h(H−h)D2√h(H+h)
An open cubical tank completely filled with water is kept on a horizontal surface. Its acceleration is then slowly increasesd to 2m/s2 as shown in the figure. The side of the tank is 1m. Find the mass of water that would spill out of the tank.

View SolutionAn open rectangular tank 1.5 m wide 2m deep ad 2 m long is half filled with water. It is accelerated horizontally at 3.27m/s2 in the direction of its length determine the depth of water at each end of tank.
View SolutionA rectangular tank is placed on a horizontal ground and is filled with water to a height H above the base. A small hole is made on one vertical side at a depth D below the level of the water in the tank. The distance x from the bottom of the tank at which the water jet from the tank will hit the ground is
View SolutionA cart supports a cubic tank filed with a liquid up to the top. The cart moves with a constant acceleration a in the horizontal direction. The tank is tightly closed. Assume that the liquid when in motion with uniform acceleration. The pressure at a point at a depth h and distance I from the front wall is :
View SolutionA tank of height 5 m/s completely filled with water. There is a hole of cross sectional area 1cm2 near its bottom. What is the initial volume of water that will come out of the hole per second. (Use g=10m/s2)
View Solution
