Answer the following question :
The motion of a simple pendulum is approximately simple harmonic for small angle oscillations. For larger angles of oscillation, a more involved analysis shows that T is greater than 2π√lg, Think of a qualitative argument to appreciate this result.Solution in Gujrati
The restoring force for the bob of the pendulum from its equilibrium position is, F=−mgsinθ
If θ is small, then sinθ≈θ hence time period of simple pendulum T=2π√lg but it θ is large then sinθ≈θ is not to be taken and hence time period of simple pendulum T=2π√lg gets slightly large.
Topper's Solved these Questions
- BOOK - KUMAR PRAKASHANCHAPTER - OSCILLATIONSEXERCISE - SECTION-B (ADDITIONAL EXERCISE)9videos
OSCILLATIONS
- BOOK - KUMAR PRAKASHANCHAPTER - OSCILLATIONSEXERCISE - SECTION-B (NUMERICAL FROM DARPAN BASED ON TEXTBOOK)15videos
OSCILLATIONS
- BOOK - KUMAR PRAKASHANCHAPTER - OSCILLATIONSEXERCISE - SECTION-B (NUMERICAL FROM TEXTUAL ILLUSTRATIONS)40videos
OSCILLATIONS
- BOOK - KUMAR PRAKASHANCHAPTER - OBJECTIVE QUESTIONS AS PER NEW PAPER STYLE EXERCISE - CHAPTER - 8 (Match Type questions)5videos
OBJECTIVE QUESTIONS AS PER NEW PAPER STYLE
- BOOK - KUMAR PRAKASHANCHAPTER - PHYSICAL WORLDEXERCISE - SECTION-E (QUESTIONS FROM MODULE)9videos
PHYSICAL WORLD
Similar Questions
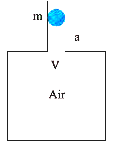
An air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.14.27). Show that when the ball is pressed down a little and released , it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27].
 09:59View Solution
09:59View SolutionThe displacement of a simple harmonic oscillator is given by y=0.40sin(440t+0.61). For this, what are the value of amplitude.
02:17View SolutionOn an average, a human heart is found to beat 75 times in a minute. Calculate its frequency and period.
09:03View SolutionType of satellites are given in Column-I and their uses are given in Column-II. Match them properly :
Column-IColumn-II(1) Polar satellite(a) Tele communication(2) Geo-stationary satellite(b) Investigation(c) For information about atmosphere04:00View Solution.…. state of substance at very high temperature has generated hope of energy source for mankind.
04:00View SolutionAnswer the following questions: (a) Time period of particle is S.H.M. depends on the force constant k and mass m of the particle :T=2π√m/k. A simple pendulum executes S.H.M. approximately. Why then is the time-period of a pendulum independent of the mass of the pendulum?
(b) The motino of simple pendulum is approximatley simple harmonic for small angles of oscillation. For large angle of oscillation, a more involved analysis (beyond the scope of this book) shows that T is greater that 2π√l/g. Think of a quanlitative argument to appreciate this result.
(c) A man with a wrist watch on his hand falls from the top of tower. Does the watch give correct time during the free fall?
(d) What is teh frequency of oscillation of a simple pendulum mounted iin a cabin that is freely falling under gravity?View SolutionAnswer the following questions: (a) The motion of a simple pendulum is approximately simple harmonic for small angle oscillation. For larger angles of oscilliation, a more involved analysis shows that T is greater than 2pisqrt((t)/(g)) Think of a qualitative argument to appreciate this result. (b) What is the frequency of oscillation of a simple pendulum mounted in a cabin that is freely falling under gravity ?
11:21View Solutionनिचे दिए गए प्रश्नों के उत्तर दीजिए :
(a) किसी कण की सरल आवर्त गति के आवर्तकाल का मान उस कण के द्रव्यमान तथा बल-स्थिरांक पर निर्भर करता है : T=2π√mk | कोई सरल लोलक सन्निकट सरल आवर्त गति करता है | तब फिर किसी लोलक का आवर्तकाल लोलक के द्रव्यमान पर निर्भर क्यों नही करता ?
(b) किसी सरल लोलक की गति छोटे कोण के सभी दोलनों के लिए सन्निकट सरल आवर्त गति होती है | बड़े कोणों के दोलनों के लिए एक अधिक गुण विश्लेषण यह दर्शाता है कि T का मान 2π√lg से अधिक होता है | इस परिणाम को समझने के लिए किसी गुणात्मक कारण का चिंतन कीजिए |
(c) कोई व्यक्ति कलाई घड़ी बाँधे किसी मीनार की चोटी से गिरता है | क्या मुक्त रूप से गिरते समय उसकी घड़ी यथार्थ समय बताती है ?
(d) गुरुत्व बल के अंतगर्त मुक्त रूप से गिरते किसी केबिन में लगे सरल लोलक के दोलन की आवर्ती क्या होती है ?05:07View Solutionनीचे दिए गए प्रश्नों के उत्तर दीजिए :
( b ) किसे सरल लोलक की गति छोटे कोण के सभी दोलनों के लिए सन्निकट सरल आवर्त गति होती है | बड़े कोणों के दोलनों के लिए एक अधिक गूढ़ विश्लेषण यह दर्शाता है कि T का मान 2π√lg से अधिक होता है |इस परिणाम को समझने के लिए किसी गुणात्मक कारण का चिंतन कीजिए |View Solutionकिसी सरल लोलक की गति छोटे कौन के सभी दोलनों के लिए एक अधिक गुड़ विश्लेषण यह दर्शाता है की T का मान 2π√lg से अधिक होता है। इस परिणाम को समझने के लिए किसी गुणात्मक कारण का चिंतन कीजिए।
02:36View Solutionनीचे दिए गए प्रश्नों के उत्तर दीजिए:
(a) किसी कण की सरल आवर्त गति के आवर्तकाल का मान उस कण के द्रव्यमान तथा बल-स्थिरांक पर निर्भर करता है: T=2π√m/k कोई सरल लोलक सन्निकट सरल आवर्त गति करता है। तब फिर किसी लोलक का आवर्तकाल लोलक के द्रव्यमान पर निर्भर क्यों नहीं करता?
(b) किसी सरल लोलक की गति छोटे कण के सभी दोलनों के लिए सन्निकट सरल आवर्त गति होती है। बड़े कोणों के दोलनों के लिए एक अधिक गूढ़ विश्लेषण यह दर्शाता है कि Tका मान 2π√ से अधिक होता है। इस परिणाम को समझने के लिए किसी गुणात्मक कारण का चिंतन कीजिए।
(c) कोई व्यक्ति कलाई घड़ी बाँधे किसी मीनार की चोटी से गिरता है। क्या मुक्त रूप से गिरते समय उसकी घड़ी यथार्थ समय बताती
(d) गुरुत्व बल के अंतर्गत मुक्त रूप से गिरते किसी केबिन में लगे सरल लोलक के दोलन की आवृत्ति क्या होती है?View SolutionShow that for a small oscillations the motion of a simple pendulum is simple harmonic. Derive an expression of its time period.
02:27View Solutionसरल लोलक की गति, अल्प दोलन कोण के लिए लगभग सरल आवर्त गति होती है। बड़े दोलन कोण के लिए आवर्तकाल Tका मान 2π√lg से अधिक होता है। इसका गुणात्मक विवेचन कीजिये।
View SolutionAnswer the following question : The motion of a simple pendulum is approximately simple harmonic for small angle oscillations. For larger angles of oscillation, a more involved analysis shows that T is greater than 2pisqrt(l/g) , Think of a qualitative argument to appreciate this result.
03:53View SolutionAnswer the following question : The motion of a simple pendulum is approximately simple harmonic for small angle oscillations. For larger angles of oscillation, a more involved analysis shows that T is greater than 2pisqrt(l/g) , Think of a qualitative argument to appreciate this result.
View Solution

