Answer the following question :
The motion of a simple pendulum is approximately simple harmonic for small angle oscillations. For larger angles of oscillation, a more involved analysis shows that T is greater than 2π√lg, Think of a qualitative argument to appreciate this result.
sinθ<θ , if the restoring force, mgsinθ is replaced by m>hη, this amounts to effective reduction in angular acceleration [Eq.(14.27)] for large angles and hence an increase in time period T over that given by the formula T=2π√lg where one assumes sinθ=θ
Topper's Solved these Questions
- BOOK - NCERT BANGLISHCHAPTER - OSCILLATIONSEXERCISE - Additional Exercises6videos
OSCILLATIONS
- BOOK - NCERT BANGLISHCHAPTER - OSCILLATIONSEXERCISE - Additional Exercises6videos
OSCILLATIONS
- BOOK - NCERT BANGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ADDITIONAL EXERCISES5videos
MOTION IN A STRAIGHT LINE
- BOOK - NCERT BANGLISHCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EXERCISES (TRUE OR FALSE)3videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
Similar Questions
Answer the following questions:
(a) The motion of a simple pendulum is approximately simple harmonic for small angle oscillation. For larger angles of oscilliation, a more involved analysis shows that T is greater than 2π√tg Think of a qualitative argument to appreciate this result.
(b) What is the frequency of oscillation of a simple pendulum mounted in a cabin that is freely falling under gravity ?View SolutionAnswer the following questions: (a) Time period of particle is S.H.M. depends on the force constant k and mass m of the particle :T=2π√m/k. A simple pendulum executes S.H.M. approximately. Why then is the time-period of a pendulum independent of the mass of the pendulum?
(b) The motino of simple pendulum is approximatley simple harmonic for small angles of oscillation. For large angle of oscillation, a more involved analysis (beyond the scope of this book) shows that T is greater that 2π√l/g. Think of a quanlitative argument to appreciate this result.
(c) A man with a wrist watch on his hand falls from the top of tower. Does the watch give correct time during the free fall?
(d) What is teh frequency of oscillation of a simple pendulum mounted iin a cabin that is freely falling under gravity?View Solution
Knowledge Check
- Question 1 - Select One
A simple pendulum suspended from the ceilling of a stationary trolley has a length l. its period of oscillation is 2π√l/g. What will be its period of oscillation if the trolley moves forward with an acceleration f ?
A2π√lf−gB2π√lf+gC2π√l(f2+g2)1/2D2π√lf2−g2 - Question 2 - Select One
A simple pendulum of length l is made to oscillate with an amplitude of 45 degrees. The acceleration due to gravity is g. Let T0=2π√l/g . The time period of oscillation of this pendulum will be -
AT0 irrespective of the amplitudeBslightly less than T0Cslightly more than T0Ddependent on whether it swings in a plane aligned with the north-south or east-west directions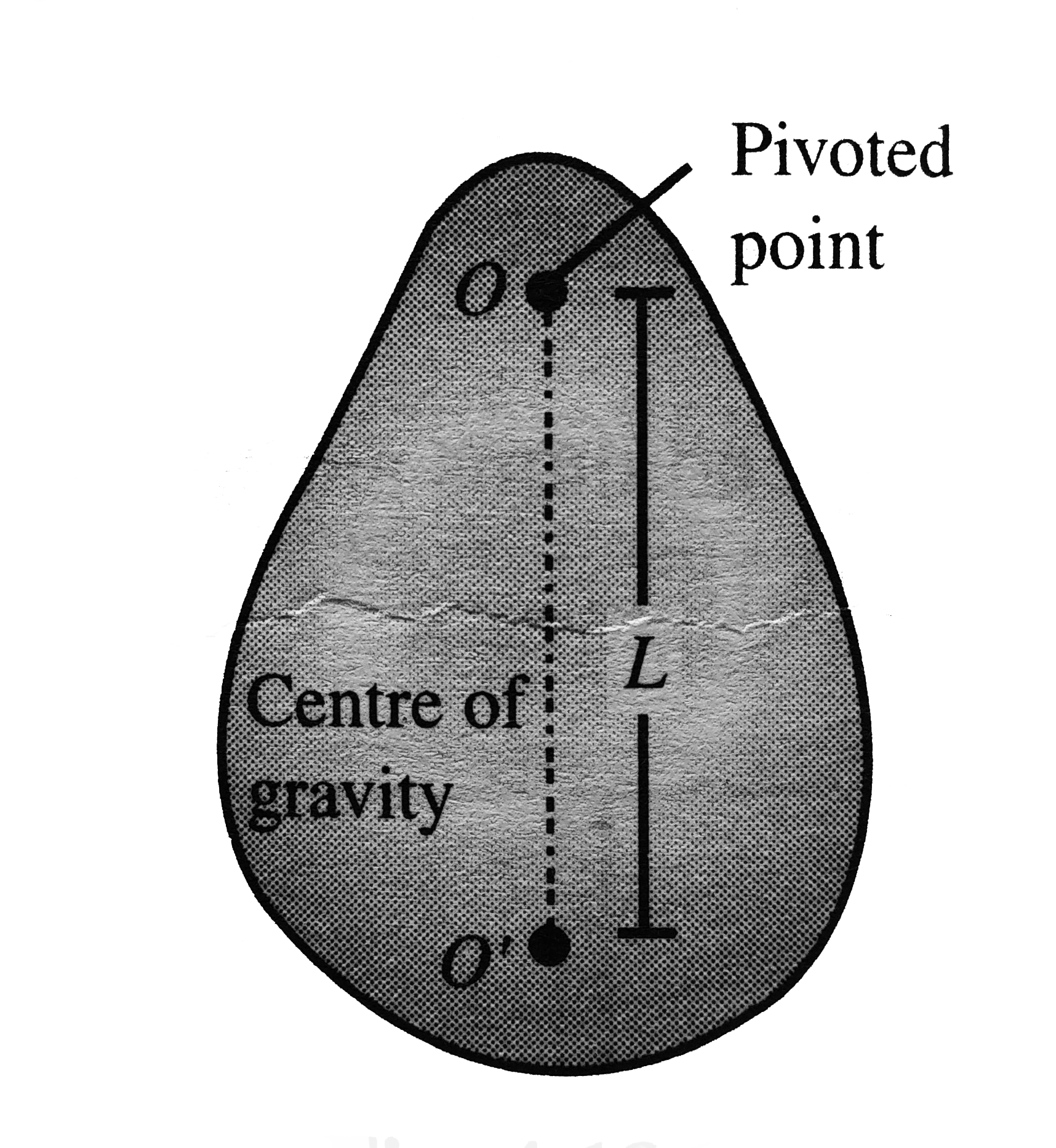 - Question 3 - Select One
In physical pendulum, the time period for small oscillation is given by T=2π√IMgd where I is the moment of inertial of the body about an axis passing through a pivoted point O and perpendicular to the plane of oscillation and d is the separation point between centre of gravity and the pivoted point. In the physical pendulum a speacial point exists where if we concentrate the entire mass of body, the resulting simple pendulum (w.r.t. pivot point O) will have the same time period as that of physical pendulum This point is termed centre of oscillation.
T=2π√IMgd=2π√Lg Moreover, this point possesses two other important remarkable properties:
Property I: Time period of physical pendulum about the centre of oscillation (if it would be pivoted) is same as in the original case.
Property II: If an impulse is applied at the centre of oscillatioin in the plane of oscillation, the effect of this impulse at pivoted point is zero. Because of this property, this point is also known as the centre of percussion. From the given information answer the following question:
Q. A uniform rod of mass M and length L is pivoted about point O as shown in Figgt It is slightly rotated from its mean position so that it performs angular simple harmonic motion. For this physical pendulum, determine the time period oscillation.A2π√LgBπ√7L3gC2π√2l3gDnone of these
Show that for a small oscillations the motion of a simple pendulum is simple harmonic. Derive an expression of its time period.
View SolutionShow that for small oscillations the motion of a simple pendulum is simple harmonic. Derive an expression for its time period. Does it depend on the mass of the bob ?
View SolutionCheck the accuracy of the relation T=2π√Lg for a simple pendulum using dimensional analysis.
View SolutionCheck the accuracy of the relation T=2π√Lg for a simple pendulum using dimensional analysis.
View Solution-
In physical pendulum, the time period for small oscillation is given by T=2π√IMgd where I is the moment of inertial of the body about an axis passing through a pivoted point O and perpendicular to the plane of oscillation and d is the separation point between centre of gravity and the pivoted point. In the physical pendulum a speacial point exists where if we concentrate the entire mass of body, the resulting simple pendulum (w.r.t. pivot point O) will have the same time period as that of physical pendulum This point is termed centre of oscillation.
T=2π√IMgd=2π√Lg Moreover, this point possesses two other important remarkable properties:
Property I: Time period of physical pendulum about the centre of oscillation (if it would be pivoted) is same as in the original case.
Property II: If an impulse is applied at the centre of oscillatioin in the plane of oscillation, the effect of this impulse at pivoted point is zero. Because of this property, this point is also known as the centre of percussion. From the given information answer the following question:
Q. A uniform rod of mass M and length L is pivoted about point O as shown in Figgt It is slightly rotated from its mean position so that it performs angular simple harmonic motion. For this physical pendulum, determine the time period oscillation.View Solution