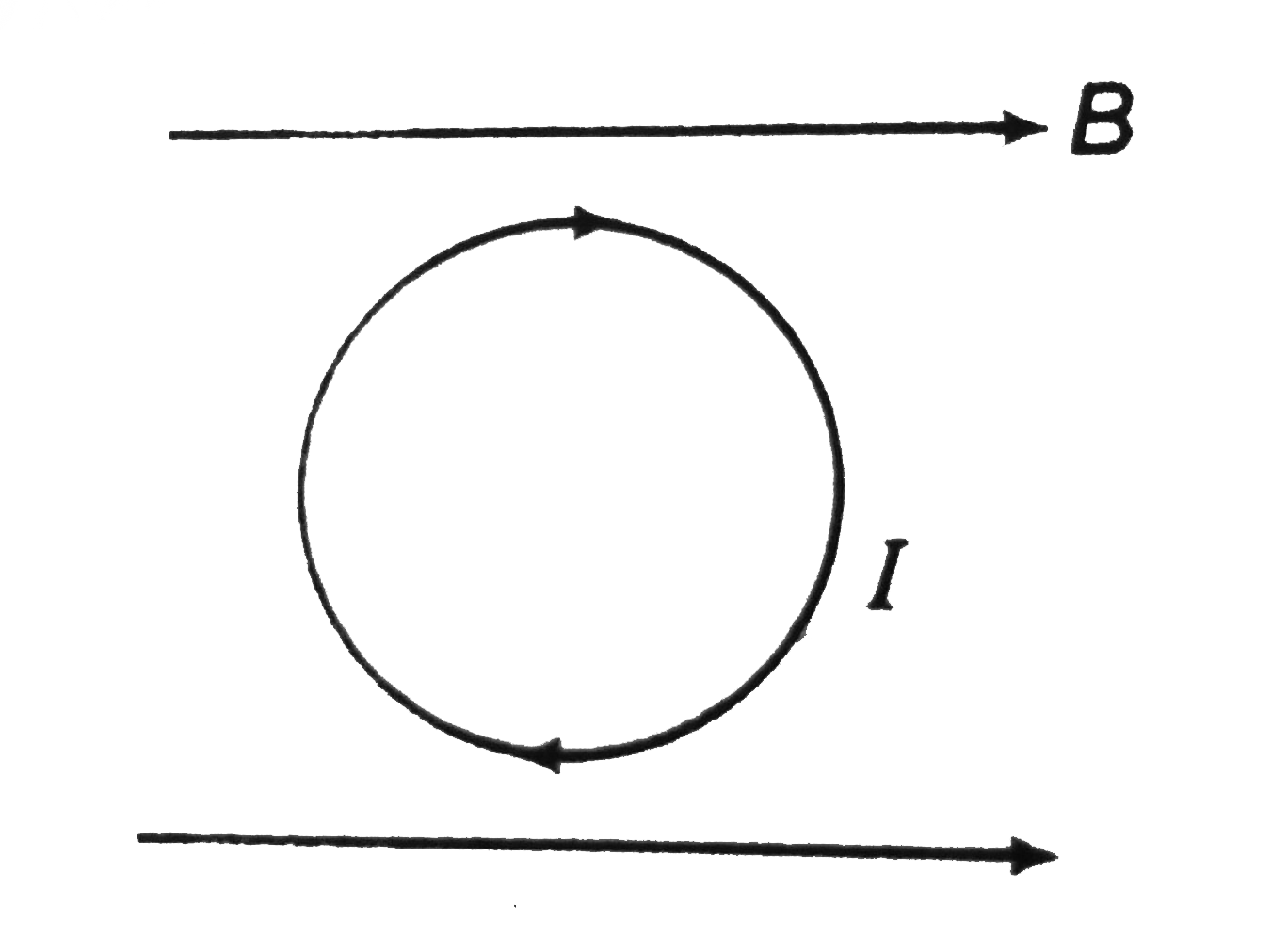
Assertion : A current carrying loop is placed in uniform magnetic field as shown in figure. Torque in the loop in this case is zero.
Reason : Magnetic moment vector of the loop is perpendicular to paper inwards.
If both Assertion and Reason are true and the Reason is correct explanation of the Assertion.
If both Assertion and Reason are true but Reason is not the correct explanation of Assertion
If Assertion is true, but the Reason is false.
If Assertion is false but the Reason is true.
The correct Answer is:D
τ=MBsin90∘≠0
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SCQ_TYPE5videos
MAGNETICS
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE1videos
MAGNETICS
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE1videos
MAGNETICS
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery59videos
MAGNETIC FIELD AND FORCES
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery1videos
MAGNETISM AND MATTER
Similar Questions
Knowledge Check
- Question 1 - Select One
A current carrying loop is placed in a uniform magnetic field. The torque acting on it does not depend upon
Aarea of loopBvalue of currentCmagnetic fieldDNone of these
Assertion Net torque in the current carrying loop placed in a uniform magnetic field (pointing inwards) is zero.

Reasonl Magnetic moment (M) is inwards.View SolutionA current carrying loop of radius R and mass 'm' is placed inside a uniform magnetic field an shown
 View Solution
View SolutionTorque acting on a current loop in a uniform magnetic field is equal to
View SolutionWill there be any tension in a current carrying loop placed in uniform magnetic field ? If yes, will it be equal to BiR ?
View SolutionA current loop in a magnetic field
View SolutionA semi circular current loop is placed in an uniform magnetic field of 1 tesla as shown. If the radius of loop is 1 m, the magnetic force on the loop is
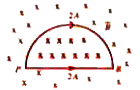 View Solution
View SolutionA current loop of arbitrary shape lies in a uniform magnetic field B. show that the net magnetic force acting on the loop is zero.
View Solution

