Assertion (A) : In a hydrogen atom the radius of nth orbit is directly proportional to the quantum number n.
Reason (R) : The speed of electron in nth orbitis inversely proportional to the quantum number.
If both assertion and reason are true and the reason is the correct explanation of the assertion.
If both assertion and reason are true but reason is not the correct explanation of the assertion.
If assertion is true but reason is false.
If the assertion is false but reason is true.
The correct Answer is:D
The reason is true but assertion is wrong. rnth∝n2.
Topper's Solved these Questions
- BOOK - U-LIKE SERIESCHAPTER - ATOMSEXERCISE - VERY SHORT ANSWER QUESTIONS.20videos
ATOMS
- BOOK - U-LIKE SERIESCHAPTER - ATOMSEXERCISE - SHORT ANSWER QUESTIONS30videos
ATOMS
- BOOK - U-LIKE SERIESCHAPTER - ATOMSEXERCISE - TRUE OR FALSE .5videos
ATOMS
- BOOK - U-LIKE SERIESCHAPTER - ALTERNATING CURRENT EXERCISE - SELF ASSESSMENT TEST (SECTION -C)2videos
ALTERNATING CURRENT
- BOOK - U-LIKE SERIESCHAPTER - CBSE EXAMINATION PAPER 2020 EXERCISE - SECTION D12videos
CBSE EXAMINATION PAPER 2020
Similar Questions
Knowledge Check
- Question 1 - Select One
Speed (Vn) of electron in nth orbit versus principal quantum number (n) graphs is
A B
B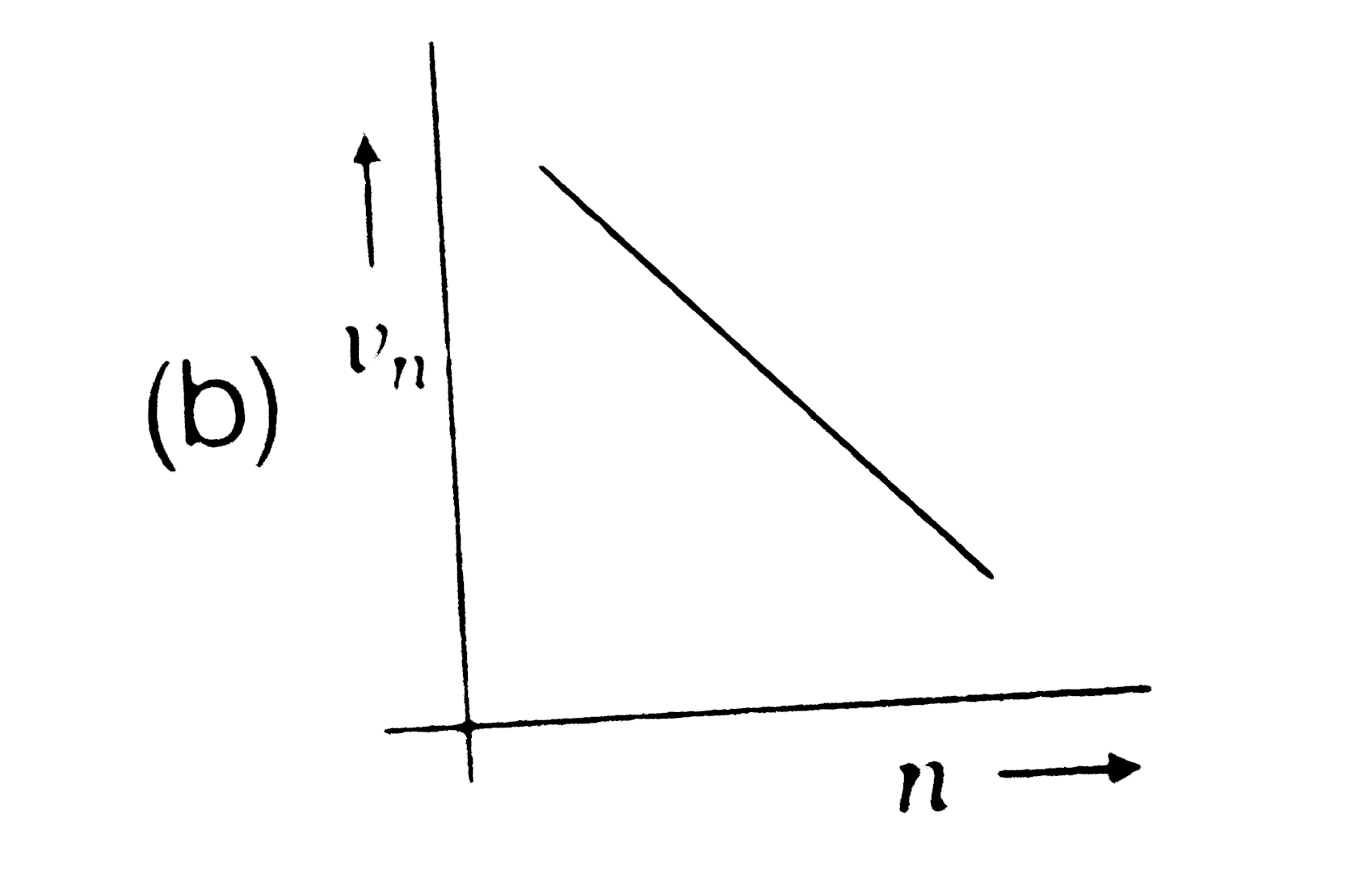 C
C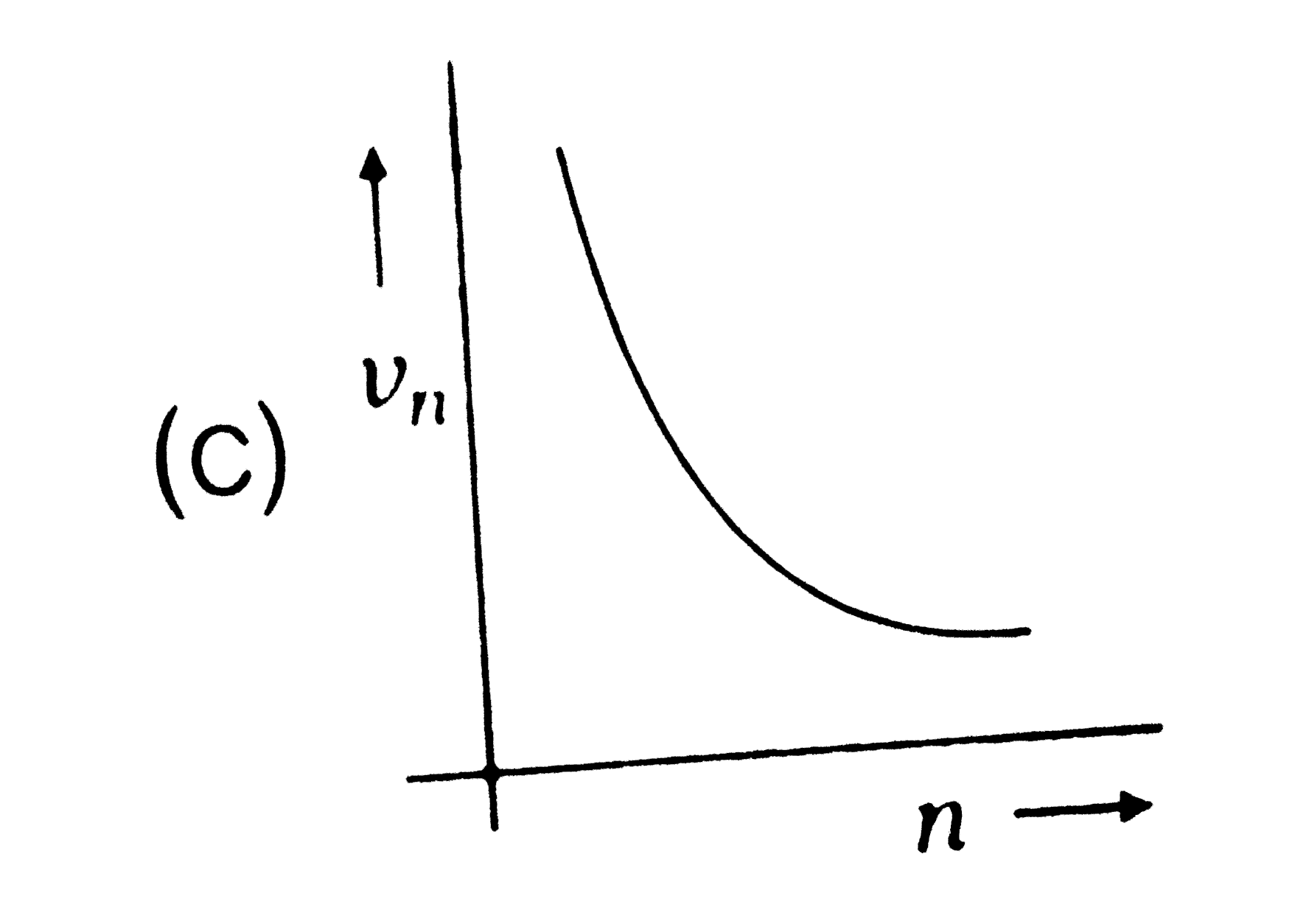 D
D
- Question 2 - Select One
If ω the speed of electron in the nth orbit hydrogen atom, then
Aω∝n1/2Bω∝1nCω∝1n2Dω∝1n3 - Question 3 - Select One
In the Bohr's hydrogen atom model, the radius of the stationary orbit is directly proportinal to (n= principle quantum number)
An−1BnCn−2Dn2
According to Bohr's atomic model the radii of stationary orbits are directly proportional to cube of the quantum number n.
View SolutionStarting with ? r= εoh2n2πmZe2, Show that the speed of electron in nth orbit varies inversely to principal quantum number.
View SolutionThe angular speed of electron in the nth orbit of hydrogen atom is
View SolutionIn the Bohr's hydrogen atom model, the radius of the stationary orbit is directly proportional to (n = principal quantum number)
View SolutionThe angular speed of electron in the nth orbit of hydrogen atom is
View Solution

