Assertion : Speed of any point on rigid body executing rolling motion can be calculated by expression v=rω, where r is distance of point from instantaneous centre of rotation
Reason : Rolling motion of rigid body can be considered as a pure rotation about instantaneous centre of rotation.
If both Assertion and Reason are correct and Reason is the correct explanation of Assertion
If both Assertion and Reason are true but Reason is not the correct explanation of Assertion
If Assertion is true but Reason is fasle
If Assertion is false but Reason is true
The correct Answer is:C
To solve the question, we need to analyze both the assertion and the reason provided.
Step 1: Understanding the Assertion
- The assertion states that the speed of any point on a rigid body executing rolling motion can be calculated using the formula v=rω, where r is the distance of the point from the instantaneous center of rotation.
- This formula is indeed valid for any point on a rigid body in rolling motion, where v is the linear speed, r is the distance from the instantaneous center of rotation, and ω is the angular velocity.
Step 2: Analyzing the Reason
- The reason claims that rolling motion of a rigid body can be considered as a pure rotation about the instantaneous center of rotation.
- While rolling motion can be analyzed in terms of rotation, not all rolling motions can be considered pure rotation. For pure rotation, the condition v=rω must hold true for all points on the body, which is not always the case in rolling motion (for example, in cases of slipping).
Step 3: Conclusion
- The assertion is true because the formula v=rω can be used to calculate the speed of any point in rolling motion.
- The reason is false because not all rolling motions satisfy the condition for pure rotation.
Final Answer:
- Assertion: True
- Reason: False
- The assertion states that the speed of any point on a rigid body executing rolling motion can be calculated using the formula v=rω, where r is the distance of the point from the instantaneous center of rotation.
- This formula is indeed valid for any point on a rigid body in rolling motion, where v is the linear speed, r is the distance from the instantaneous center of rotation, and ω is the angular velocity.
- The reason claims that rolling motion of a rigid body can be considered as a pure rotation about the instantaneous center of rotation.
- While rolling motion can be analyzed in terms of rotation, not all rolling motions can be considered pure rotation. For pure rotation, the condition v=rω must hold true for all points on the body, which is not always the case in rolling motion (for example, in cases of slipping).
- The assertion is true because the formula v=rω can be used to calculate the speed of any point in rolling motion.
- The reason is false because not all rolling motions satisfy the condition for pure rotation.
- Assertion: True
- Reason: False
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (A) Chapter Exercises
83 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
Knowledge Check
Assertion: The motion of a ceiling fan is rotational only.
Reason: The motion of a rigid body which is pivoted fixed of rotation.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertionCIf assertion is true but reason is false.DIf both assertion and reason are false.A sphere cannot roll on a smooth inclined surface.
The motion of a rigid body which is pivoted or fixed in some way is rotation.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertionCIf assertion is true but reason is false.DIf both assertion and reason are false.Assertion: A rigid body not fixed in some way can have either pure translation or a combination of translation and rotation.
Reason: In rotation about a fixed axis, every particle of the rigid body moves in a circle which lies in a plane perpendicular to the axis and has its centre on the axis.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertionCIf assertion is true but reason is false.DIf both assertion and reason are false.
A disc of radius 0.2m is rolling with slipping on a flat horizontal surface, as shown in Fig. The instantaneous centre of rotation is (the lowest contact point is O and centre of disc is C)
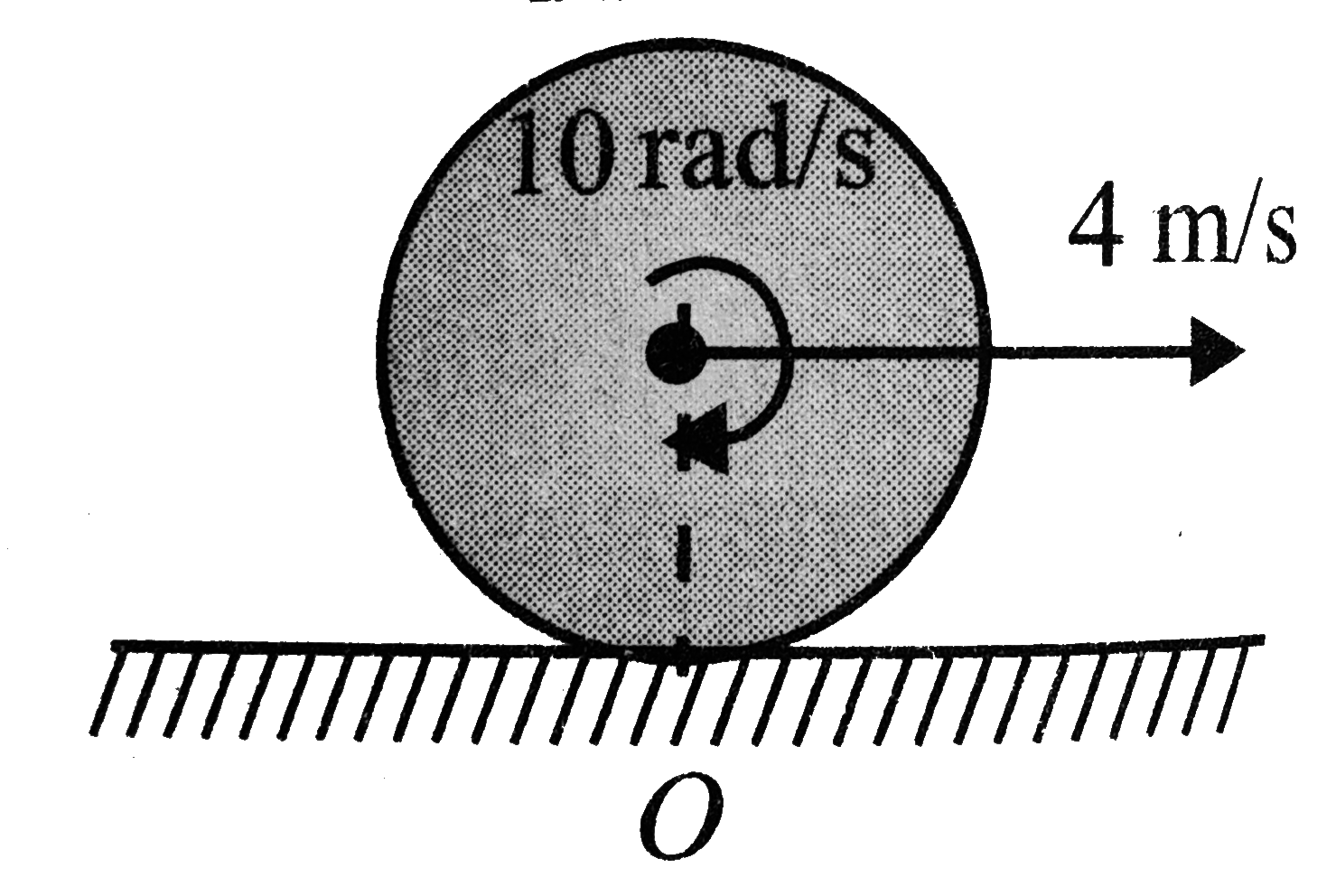
View SolutionA sphere is moving at some instant with horizontal velocity v0 in right and angular velocity ω in anti clockwise sense. If |v0|=|ωR|, the instantaneous centre of rotation is
View SolutionA body at rest starts from a point at a distance r (gtR) from the centre of the Earth. If M and R stand for the speed of the body when it reaches the Earth surface is
View SolutionA : rigid body can't be in a pure rolling on a rough inclined plane without giving any external force.
R : Since there is no torque providing force acting on the body in the above case, the body can't come in a rolling condition.
View SolutionAssertion : The moment of inertia of a rigid body reduces to its minimum value, when the axis of rotation passes through its centre of gravity.
Reason : The weight of a rigid body always acts through its centre of gravity.
View Solution
