Assertion Two concentric conducting rings of different radii are placed in space. The mutual inductance of both the rings is maximum, if the rings are coplanar.
Reason For two co-axial conducting rings of different radii, the magnitude of magnetic flux in one ring due to current in other ring is maximum when both rings are coplanar.
If both Assertion and Reason are corrent and Reason is the corrent explanation of Assertion.
If both Assertion and Reason are correct but Reason is not the correct explanation of Assertion.
If Assertion is true but Reason is false.
If Assertion is false but Reason is ture.
The correct Answer is:A
To solve the given question, we need to analyze the assertion and the reason provided regarding the mutual inductance of two concentric conducting rings.
1. Understanding Mutual Inductance:
- Mutual inductance (M) is a measure of how much the magnetic flux in one coil changes due to the current in another coil. It depends on the geometry and relative positioning of the coils.
2. Assertion Analysis:
- The assertion states that two concentric conducting rings of different radii have maximum mutual inductance when they are coplanar.
- When the rings are coplanar, the magnetic field lines produced by the current in one ring effectively link with the other ring, maximizing the magnetic flux through it.
3. Reason Analysis:
- The reason states that for two coaxial conducting rings of different radii, the magnetic flux in one ring due to the current in the other is maximum when both rings are coplanar.
- This is true because the magnetic field generated by one ring is strongest in the plane of the ring itself, and thus, when both rings are in the same plane, the magnetic flux linkage is maximized.
4. Conclusion:
- Both the assertion and reason are correct statements. The reason correctly explains why the assertion is true. Therefore, the mutual inductance is indeed maximum when both rings are coplanar.
5. Final Answer:
- Since both statements are correct and the reason is the correct explanation for the assertion, the answer is Option A.
- Mutual inductance (M) is a measure of how much the magnetic flux in one coil changes due to the current in another coil. It depends on the geometry and relative positioning of the coils.
- The assertion states that two concentric conducting rings of different radii have maximum mutual inductance when they are coplanar.
- When the rings are coplanar, the magnetic field lines produced by the current in one ring effectively link with the other ring, maximizing the magnetic flux through it.
- The reason states that for two coaxial conducting rings of different radii, the magnetic flux in one ring due to the current in the other is maximum when both rings are coplanar.
- This is true because the magnetic field generated by one ring is strongest in the plane of the ring itself, and thus, when both rings are in the same plane, the magnetic flux linkage is maximized.
- Both the assertion and reason are correct statements. The reason correctly explains why the assertion is true. Therefore, the mutual inductance is indeed maximum when both rings are coplanar.
- Since both statements are correct and the reason is the correct explanation for the assertion, the answer is Option A.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Match the columns5videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery25videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Taking it together119videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery97videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
Similar Questions
A circular conducting ring is rotated about one of its diameter in a magnetic field
View SolutionA battery is connected between two points AandB on the circumference of a uniform conducting ring of radius r and resistance R . One of the arcs AB of the ring subtends an angle θ at the centre . The value of the magnetic induction at the centre due to the current in the ring is
View Solution
Knowledge Check
- Question 1 - Select One or More
In which of the following molecules both phenyl rings are coplanar>?
A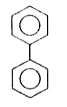 B
B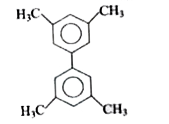 C
C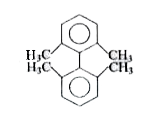 D
D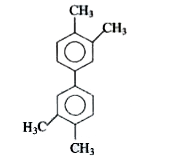
- Question 2 - Select One
A conducting ring is placed in a uniform magnetic field with its plane perpendicular to the field . An emf is induced in the ring if
Ait is rotated about its axis.Bit is rotated about its diameter.Cit is not moved.Dit is given translational motion in the field.
Three rings, each having radius R, are placed mutually perpendicular to each other and each having its centre at the origin of co-ordinate system. If current I is flowing through each ring then the magnitude of the magnetic field at the common centre is:
View SolutionThree rings, each having equal radius R, are placed mutually perpendicular to each other and each having its centre at the origin of coordinate system. If current I is flowing through each ring, then the magnitude of the magnetic field at the common centre is
 View Solution
View SolutionThree rings, each having equal radius R, are placed mutually perpendicular to each other and each having its centre at the origin of coordinate system. If current I is flowing through each ring, then the magnitude of the magnetic field at the common centre is
 View Solution
View SolutionThree rings, each having equal radius R, are placed mutually perpendicular to each other and each having its centre at the origin of coordinate system. If current I is flowing through each ring, then the magnitude of the magnetic field at the common centre is
 View Solution
View SolutionThe diagram given below shows a solenoid carrying time varying current l=l0t. On the axis of the solenoid, a ring has been placed. The mutual inductance of the ring and the solenoid is M and the self inductance of the ring is L. If the resistance of the ring is R then maximum current which can flow through the ring is
 View Solution
View SolutionA metallic ring hangs vertically from a thread with its axis pointing E−W. A coil is fixed near to the ring and co-axial with it. When current in the coil is switch on,then the ring
_PHY_E06_295 _Q01.png) View Solution
View Solution

