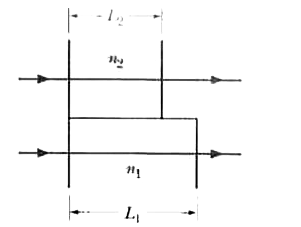
Assume that two waves of light in air, of wavelength 585 nm, are initially in phase. One travels through a glass layer of index of refraction n1=160 and thickness L. The other travels through an equally thick plastic layer of index of refraction n2=1.50. (a) What is the smallest value L should have if the waves are to end up with a phase difference of 5.65 rad? (b) If the waves arrive at some common point with the same amplitude, is their interference fully constructive, fully destructive, intermediate but closer to fully constructive, or intermediate but closer to fully destructive?
(a) 5.26 mm, (b) intermediate closer to fully constructive
Topper's Solved these Questions
- INTERFERENCE AND DIFFRACTION BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type)
66 Videos
- INTERFERENCE AND DIFFRACTION BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type)
23 Videos
- INTERFERENCE AND DIFFRACTION BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - CHECKPOINT
6 Videos
- HYDROGEN ATOMBOOK - RESNICK AND HALLIDAYCHAPTER - HYDROGEN ATOMEXERCISE - PRACTICE QUESTIONS(Integer Type)
6 Videos
- MAGNETIC FIELDS DUE TO CURRENTSBOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FIELDS DUE TO CURRENTSEXERCISE - Practice Question (Integer Type)
4 Videos
Similar Questions
Two waves of light in air, of wavelength λ=600.0nm, are initially in phase. They then both travel through a layer of plastic as shown in Figure, with L_(1)= 4.00 mu m, L_(2)= 3.50 mu m, n_(1) = 1.42, and n2=1.60. (a) What multiple of λ gives their phase difference after they both have emerged from the layers? (b) If the waves later arrive at some common point with the same amplitude, is their interference fully constructive, fully destructive, interme- diate but closer to fully constructive, or intermediate but closer to fully destructive?
View SolutionIf v is the velocity of light in air or vacuum, find the time taken by the light to travel through a glass slab of thickness x and having refraction index μ.
View Solution
Knowledge Check
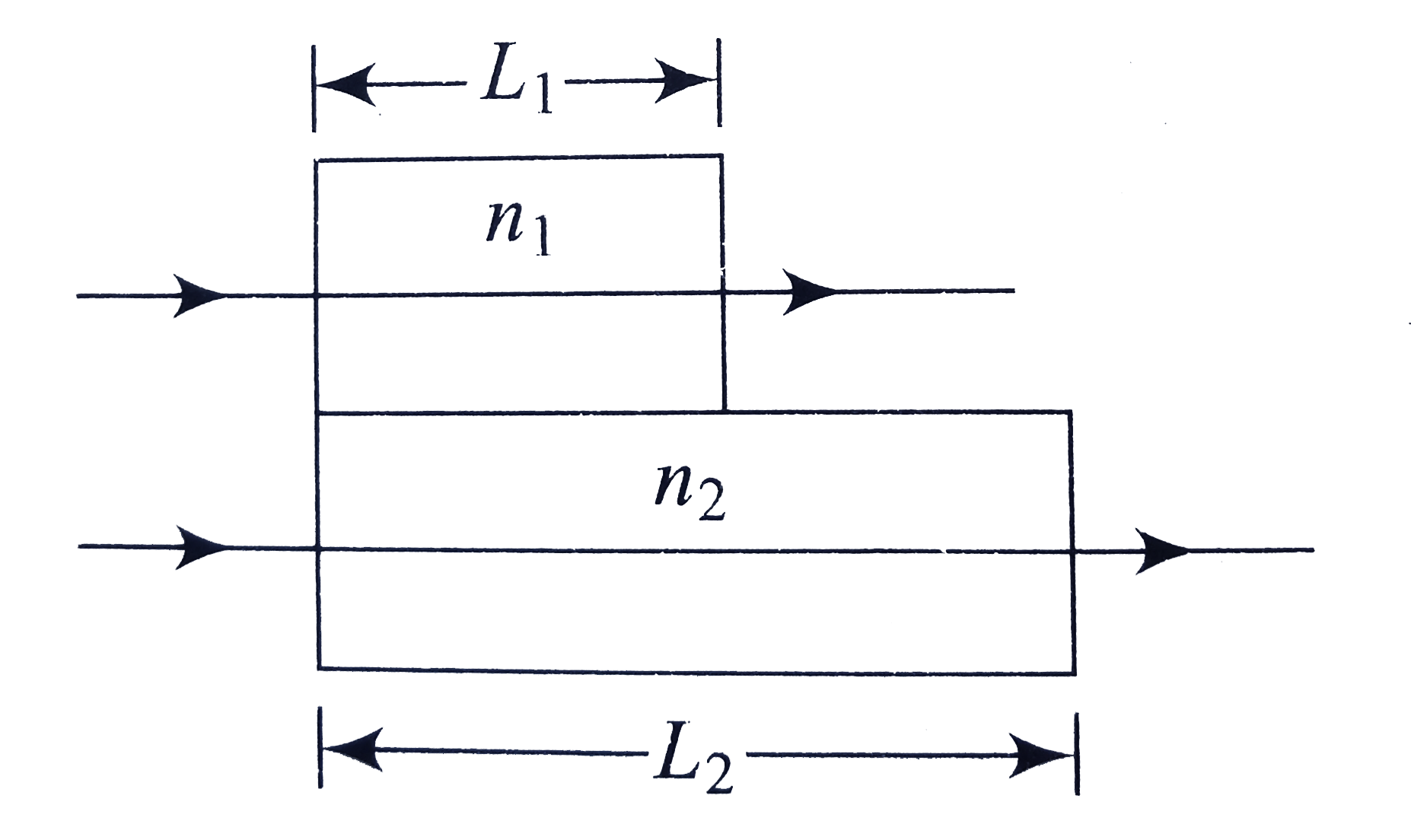
Two waves of light in air have the same wavelength and are intially in phase. They then travel through plastic layers with thickness of L1=3.5mm and L2=5.0mm and indices of refraction n1=1.7 and n2=1.25 as shown in figure. The rays later arrive at a common point. The longest wavelength of light for which constructive interference occurs at the point is
 A0.8μmB1.2μmC1.7μmD2.9μm
A0.8μmB1.2μmC1.7μmD2.9μmThe time taken by a ray of light to travel through a glass slab of thickness 2 cm and refractive index 1.5 will be
A10^(-8) sB10−10sC2×10−8sD10−12sIf c is the velocity of light in vacuum, then find the time taken by the light to travel through a glass plane of thickness t and having refractive index μ.
A(tμc)BtμcCμtcDtcμ
Two waves of light in air have the same wavelength and are intially in phase. They then travel through plastic layers with thickness of L1=3.5mm and L2=5.0mm and indices of refraction n1=1.7 and n2=1.25 as shown in figure. The rays later arrive at a common point. The longest wavelength of light for which constructive interference occurs at the point is

View SolutionAssume that the two light waves, of wavelength 515 nm in air, are initially out of phase by π rad. The indexes of refraction of the media are n1=1.45 and n2=1.75. What are the (a) smallest and (b) second smallest value of L that will put the waves exactly in phase once they pass through the two media?
View SolutionCalculate the time which light will take to travel normally through a glass plate of thickness 1mm. Refractive index of glass is 1.5.
View SolutionLight travels through a glass plate of thickness t and refractive index μ. If c is the speed of light in vacuum, the time taken by light to travel this thickness of glass is
View SolutionBlue light with a wavelength of 425 nm passes from a vacuum into a glass lens, and the index of refraction is found to be 1.65. The glass lens is replaced with a plastic lens. The index of refraction for the plastic lens is 1.54. In which one of the two lenses does the light have the greatest speed and what is that speed ?
View Solution
