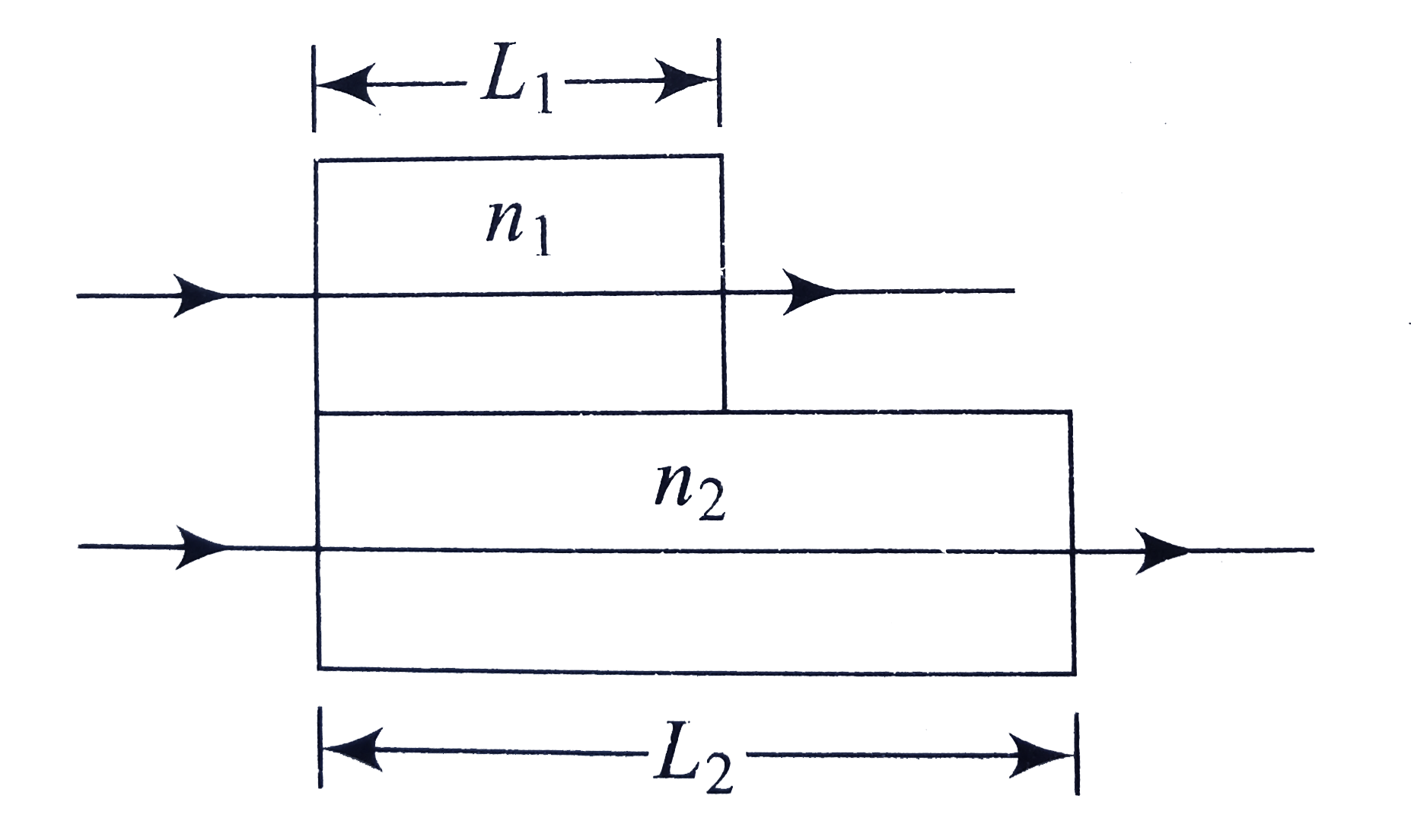
Two waves of light in air have the same wavelength and are intially in phase. They then travel through plastic layers with thickness of L1=3.5mm and L2=5.0mm and indices of refraction n1=1.7 and n2=1.25 as shown in figure. The rays later arrive at a common point. The longest wavelength of light for which constructive interference occurs at the point is
0.8mm
1.2mm
1.7mm
2.9mm
The correct Answer is:b
Δx=path difference between two light waves
=[n1L1+L2−L1]−[n2L2]
Δϕ= phase difference between two waves
For longest wavelengths, Δϕ is the smallest.
For constructive interference, Δϕ=2π
Imax=n1L1−n2L2+(L2−L1)
(1.7)(3.5×10−6)−(1.25)(5.0×10−6)
+(5.0−3.5)×10−6
=(5.95−6.25+1.5)×10−6=1.2510−6m
=1.2μm
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Multiple Correct
8 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Subjective
11 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
Similar Questions
_E01_030_Q01.png)
A light wave travels through three transparent materials of equal thickness rank in order from the highest to lowest the indices of refraction n1,n2 and n3.
View SolutionTwo light waves having the same wavelength λ in vacuum are in phase initially. Then the first ray travels a path of length L1 through a medium of refractive index μ1. Then second ray travels a path of length L2 throug a medium of refractive index μ2. The two waves are then combined to observed interference effects. The phase difference between the two, when they interfere, is
View SolutionTwo light waves having the same wavelength λ in vacuum are in phase initially. Then the first ray travels a path of length L1 through a medium of refractive index μ1. Then second ray travels a path of length L2 throug a medium of refractive index μ2. The two waves are then combined to observed interference effects. The phase difference between the two, when they interfere, is
View SolutionTwo identical light sources S1 and S2 emit light of same wavelength λ. These light rays will exhibit interference if
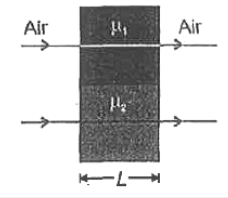
View SolutionTwo light rays initially in same phase travel through two media of equal length L having refraction index μ1andμ2(μ1>μ2) as shown in figure. If the wavelength of light rays in air is λ, the phase difference of the emerging rays is given by
View SolutionThe time required to pass the light through a glass slab of 2 mm thick is (μglass=1.5)
View SolutionThe wavelength of light in vacuum is 5000Å when it travels normally through diamond of thickness 1.0 mm find the number of waves of light in 1.0 mm of diamond. (Refractive index of diamond =2.417)
View SolutionThin films, including soap bubbles and oil show patterns of alternative dark and bright regions resulting from interference among the reflected ligth waves. If two waves are in phase, their crests and troughs will coincide. The interference will be cosntructive and the amlitude of resultant wave will be greater then either of constituent waves. If the two wave are not of phase by half a wavelength (180∘), the crests of one wave will coincide width the troughs of the other wave. The interference will be destructive and the ampliutde of the resultant wave will be less than that of either consituent wave.
1. When incident light I, reaches the surface at point a, some of the ligth is reflected as ray Ra and some is refracted following the path ab to the back of the film.
2. At point b, some of the light is refracted out of the film and part is reflected back through the film along path bc. At point c, some of the light is reflected back into the film and part is reflected out of the film as ray Rc.
Ra and Rc are parallel. However, Rc has travelled the extra distance within the film fo abc. If the angle of incidence is small, then abc is approxmately twice the film's thickness .
If Ra and Rc are in phase, they will undergo constructive interference and the region ac will be bright. If Ra and Rc are out of phase, they will undergo destructive interference and the region ac will be dark.
I. Refraction at an interface never changes the phase of the wave.
II. For reflection at the interfere between two media 1 and 2, if n1>n2, the reflected wave will change phase. If n1<n2, the reflected wave will not undergo a phase change.
For reference, nair=1.00.
III. If the waves are in phase after reflection at all intensities, then the effects of path length in the film are:
Constrictive interference occurs when 2t=mλ/n,m=0,1,2,3,...
Destrcutive interference occurs when 2t=(m+12)λn,
m=0,1,2,3,...
If the waves are 180∘ out of the phase after reflection at all interference, then the effects of path length in the film ara:
Constructive interference occurs when
2t=(m+12)λn,m=0,1,2,3,...
Destructive interference occurs when
2t=mλn,m=0,1,2,3,...
The average human eye sees colors with wavelength between 430 nm to 680 nm. For what visible wavelength (s) will a 350 nm thick (n=1.35) soap film produce maximum destructive interference?
View SolutionA ray of light coming fromthe point (1, 2) is reflected at a point A on the x-axis and then passes through the point (5,3). The coordinates of the point A is :
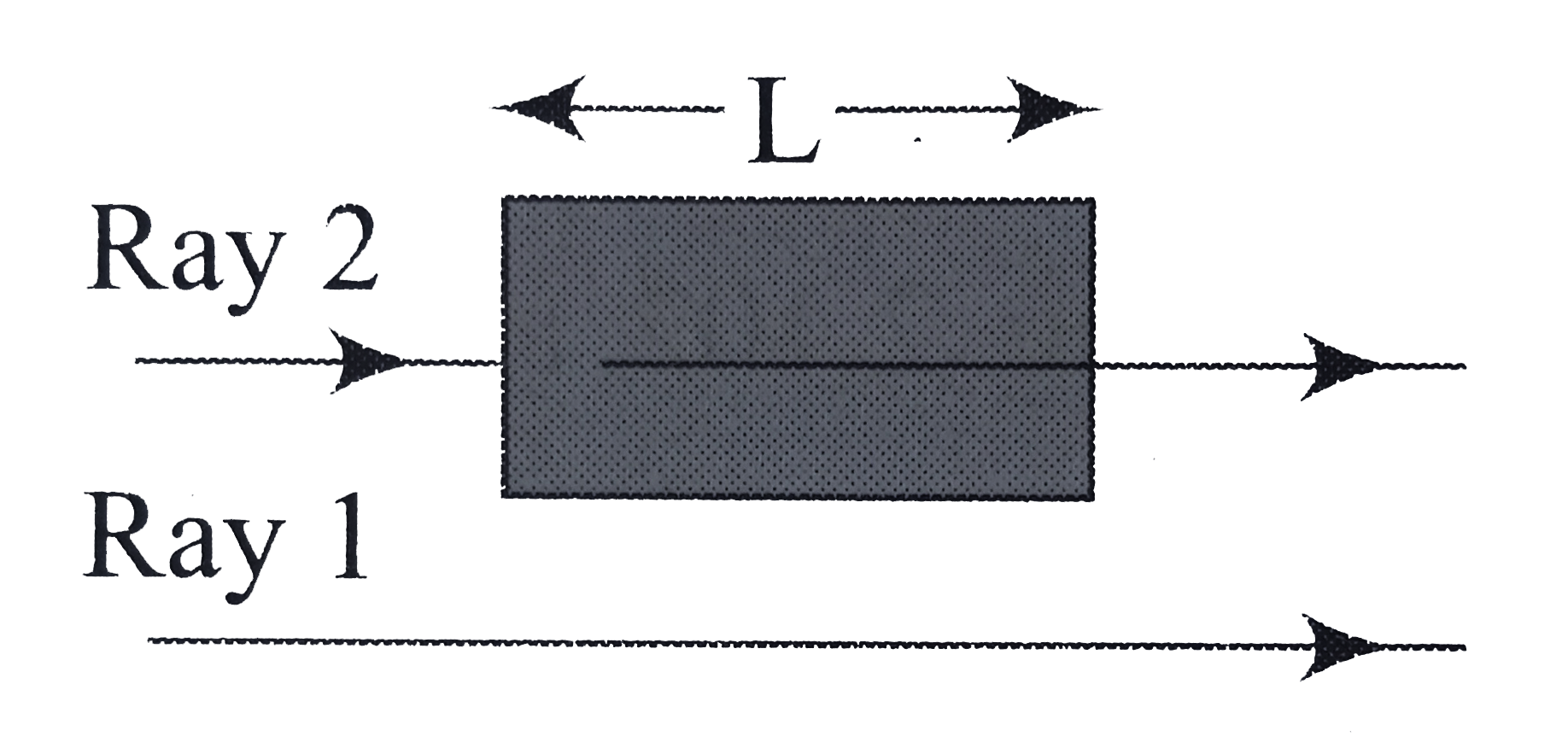
View SolutionAs shown in figure waves with identical wavelengths and amplitudes and which are intially in phase travel through difference media. Ray 1 travels through air and Ray 2 through a transparent medium for equal length L, in four different situations. Rays reach a common point on the screen. The number of wavelengths in length L is N2 for Ray 2 and N1 for Ray 1. In the following table, values of N1 and N2 are given for all four situations. The order or the situations according to the intensity of the light at the common point in descending order is Situations
1 2 3 4
N1 2.75 1.80 3.00 3.25
N2 2.75 2.80 3.25 4.00
View Solution


