In Figure, two light rays go through different paths by reflecting from the various flat surfaces shown. The light waves have a wavelength of 411.0 nm and are initially in phase. What are the (a) smallest and (b) second smallest value of distance L that will put the waves exactly out of phase as they emerge from the region?
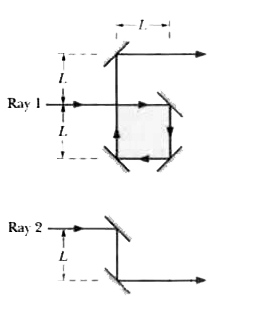
(a) 51.38 nm, (b) 154.1 nm
Topper's Solved these Questions
- INTERFERENCE AND DIFFRACTION BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type)
66 Videos
- INTERFERENCE AND DIFFRACTION BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type)
23 Videos
- INTERFERENCE AND DIFFRACTION BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - CHECKPOINT
6 Videos
- HYDROGEN ATOMBOOK - RESNICK AND HALLIDAYCHAPTER - HYDROGEN ATOMEXERCISE - PRACTICE QUESTIONS(Integer Type)
6 Videos
- MAGNETIC FIELDS DUE TO CURRENTSBOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FIELDS DUE TO CURRENTSEXERCISE - Practice Question (Integer Type)
4 Videos
Similar Questions
In Figure, a light wave along ray r1 reflects once from a mirror and a light wave along ray r2 reflects twice from that same mirror and once from a tiny mirror at distance L from the bigger mirror. (Neglect the slight tilt of the rays.) The waves have wavelength 350 nm and are initially in phase. (a)What is the smallest value of L that puts the final light waves exactly out of phase? (b) With the tiny mirror initially at that value of L, how far must it be moved away from the bigger mirror to again put the final waves out of phase?
View SolutionAssume that the two light waves, of wavelength 515 nm in air, are initially out of phase by π rad. The indexes of refraction of the media are n1=1.45 and n2=1.75. What are the (a) smallest and (b) second smallest value of L that will put the waves exactly in phase once they pass through the two media?
View Solution
Knowledge Check
Figure shows two light rays that are initially exactly in phase and that reflect from several glass surfaces. Neglect the slight slant in the path of the light in the second arrangement. The path length difference in terms of wavelength λ is :
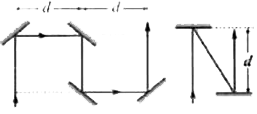A2dB(d+λ)C(2d+λ)Dnone of theseTwo point A and B are situated at the same distance from the phase difference between the light waves passing throught A and B will be
AzeroBπ/2CπD2π/3The displacement of a vibrating string versus position along the string is shown in the figure. The periodic wave have a speed of 10.0cm/s. A and B are two points on the string.
What is the difference in phase between the points A and B?A(π/4) radiansB(π/2) radiansCπ radiansD(3π/4) radians
In Fig., sound waves A and B, both of wavelength λ , are initially in phase and traveling rightward, as indicated by the two rays. Wave A is reflected from four surfaces but ends up traveling in its original direction. Wave B ends in that direction after reflecting from two surfaces. Let distance L in the figure be expressed as a multiple q of λ:L=qλ. What are the (a) smallest and (b) third smallest values of q that put A and B exactly out of phase with each other after the reflections?
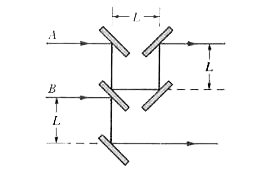
View Solution
In Figure, a light wave along ray r1 reflects once from a mirror and a light wave along ray r2 reflects twice from that same mirror and once from a tiny mirror at distance L from the bigger mirror. (Neglect the slight tilt of the rays.) The waves have wavelength λ and are initially exactly out of phase. What are the (a) smallest. (b) second smallest, and (c) fourth smallest values of L/λ that result in the final waves being exactly in phase?
View SolutionIn Fig. , the two light waves that are represented by the rays have wavelength 550.0 nm before entering media 1 and 2. They also have equal amplitudes and are in phase. Medium 1 is now just air, and medium 2 is a transparent plastic layer of index of refraction 1.600 and thickness 2.600 μm.
If the waves reached the same point on a distant screen, what type of interference would they produce?
View Solution_E01_089_Q01.png)
Thin films, including soap bubbles and oil slicks, show patterns of alternating dark and bright regions resulting from interference among the reflected light waves. If two waves are in phase their crest and troughs will coincide. The interference will be constructive and the aplitude of the resultant wave will be greater than the amplitude of either constituent wave. if the two waves are out of phase, the crests of one wave will coincide with the troughs of the other wave. The interference will be destructive and the amplitude of the resultant wave will be less than that of either constituent wave. at the interface between two transparent media some light is reflected and some light is refracted.
* When incident light, reaches the surface at point a, some of the light is reflected as ray Ra and and some is refracted following the path ab to the back of the film.
*At point b some of the light is refracted out of the film and part is reflected back refracted out of the fiml as ray Rc. Ra and Rc are parallel. However, Rc has travelled the extra distance within the film of abc. if the angle of incidence is small then abc is approximately twice the film's thickness. if Ra and Rc are in phase they will undergo constructive interference and the region ac will be bright if Ra and Rc are out of phase, they will undergo destructive interference.
* Refraction at an interface never changes the phase of the wave.
* For reflection at the interface between two media 1 and 2, if n1<n2 the reflected wave will change phase by π.
if n1>n2 the reflected wave will not undergo a phase change. for reference nair=1.00
* if the waves are in phase after refection at all interfaces, then the effects of path length in the film are
Constructive interference occur when (n= refractive index) 2t=mλ/n m=0,1,2,3.....
Destructive interference occurs when 2t=(m+1/2)λ/n m=0,1,2,3...
Q. The average human eye sees colors with wavelengths between 430 nm to 680 nm. For what visible wavelength will a 350 nm thick n=1.35 soap film produce maximum destructive interference?
View Solution_E01_090_Q01.png)
Thin films, including soap bubbles and oil slicks, show patterns of alternating dark and bright regions resulting from interference among the reflected light waves. If two waves are in phase their crest and troughs will coincide. The interference will be constructive and the aplitude of the resultant wave will be greater than the amplitude of either constituent wave. if the two waves are out of phase, the crests of one wave will coincide with the troughs of the other wave. The interference will be destructive and the amplitude of the resultant wave will be less than that of either constituent wave. at the interface between two transparent media some light is reflected and some light is refracted.
* When incident light, reaches the surface at point a, some of the light is reflected as ray Ra and and some is refracted following the path ab to the back of the film.
*At point b some of the light is refracted out of the film and part is reflected back refracted out of the fiml as ray Rc. Ra and Rc are parallel. However, Rc has travelled the extra distance within the film of abc. if the angle of incidence is small then abc is approximately twice the film's thickness. if Ra and Rc are in phase they will undergo constructive interference and the region ac will be bright if Ra and Rc are out of phase, they will undergo destructive interference.
* Refraction at an interface never changes the phase of the wave.
* For reflection at the interface between two media 1 and 2, if n1<n2 the reflected wave will change phase by π.
if n1>n2 the reflected wave will not undergo a phase change. for reference nair=1.00
* if the waves are in phase after refection at all interfaces, then the effects of path length in the film are
Constructive interference occur when (n= refractive index) 2t=mλ/n m=0,1,2,3.....
Destructive interference occurs when 2t=(m+1/2)λ/n m=0,1,2,3...
Q. A 600 nm light is perpendicularly incident on a soap film suspended in air. The film is 1.00 μm thick with n=1.35. Which statement most accurately describes the interference of the light reflected by the two surfaces of the film?
View Solution