At each point on the surface of the cube shown in Fig. 23-47, the electric field is parallel to the z axis. The length of each edge of the cube is 4.0 m. On the top face of the cube the field is →E=−34ˆk N/C, and on the bottom face it is →E=+20ˆk N/C Determine the net charge contained within the cube.
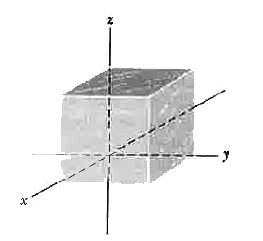
−7.6×10−9C
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - GAUSS' LAW EXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)20videos
GAUSS' LAW
- BOOK - RESNICK AND HALLIDAYCHAPTER - GAUSS' LAW EXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)2videos
GAUSS' LAW
- BOOK - RESNICK AND HALLIDAYCHAPTER - GAUSS' LAW EXERCISE - CHECKPOINT7videos
GAUSS' LAW
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)1videos
FORCE AND MOTION-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFLECTION EXERCISE - PRACTICE QUESTIONS (Integer Type)3videos
GEOMETRICAL OPTICS : REFLECTION
Similar Questions
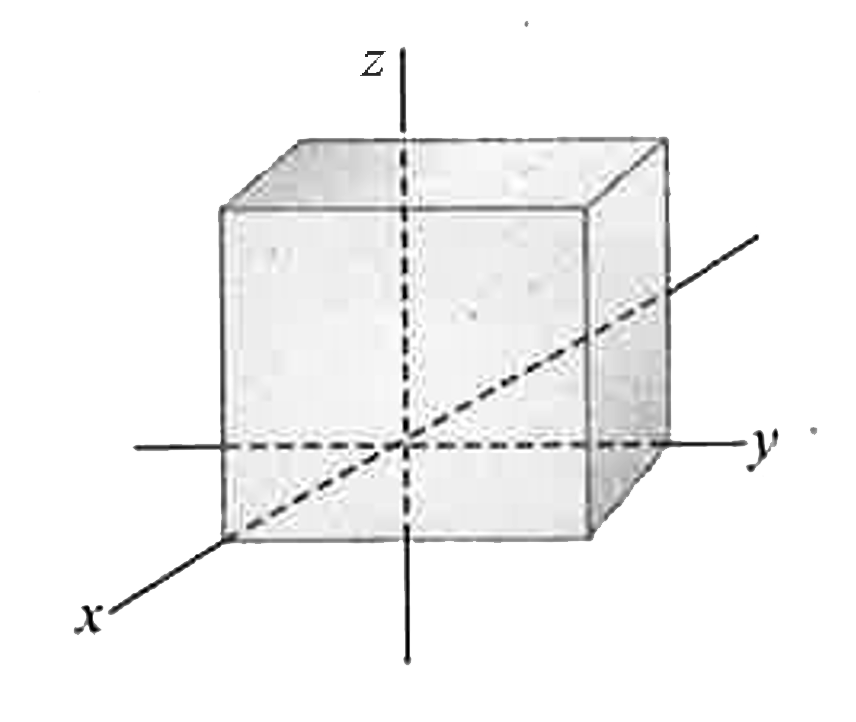
At each point on the surface of the cube shown in the figure, the electric field is parllel to the z- axis. The length of each edge of the cube is 3.0 m on the bottom face it is →E=34ˆkN/C and on the bottom face it is →E=20ˆkN/C . Find the net flux contained within the cube.
 View Solution
View SolutionAt each point on the surface of the cube shown in the figure, the electric field is parllel to the z- axis. The length of each edge of the cube is 3.0 m on the bottom face it is →E=34ˆkN/C and on the bottom face it is →E=20ˆkN/C . Find the net flux contained within the cube.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A charge qμC is placed at the centre of a cube of a side 0.1m, then the electric flux diverging from each face of the cube is
Aq×10−624ε0Bq×10−4ε0Cq×10−66ε0Dq×10−412ε0 - Question 2 - Select One
A charge of q μC is placed at the centre of a cube of side 0.1 m. the electric flux diverging from each face of the cube will be
Aq×10−6ε0 VmBq×10−66ε0 VmC6q×10−6ε0VmDq×10−4(ε0)Vm
A charge qμC is placed at the centre of a cube of a side 0.1m, then the electric flux diverging from each face of the cube is
View SolutionThe electric field in a cubical volume is
→E=E0(1+za)ˆi+E0(za)ˆj
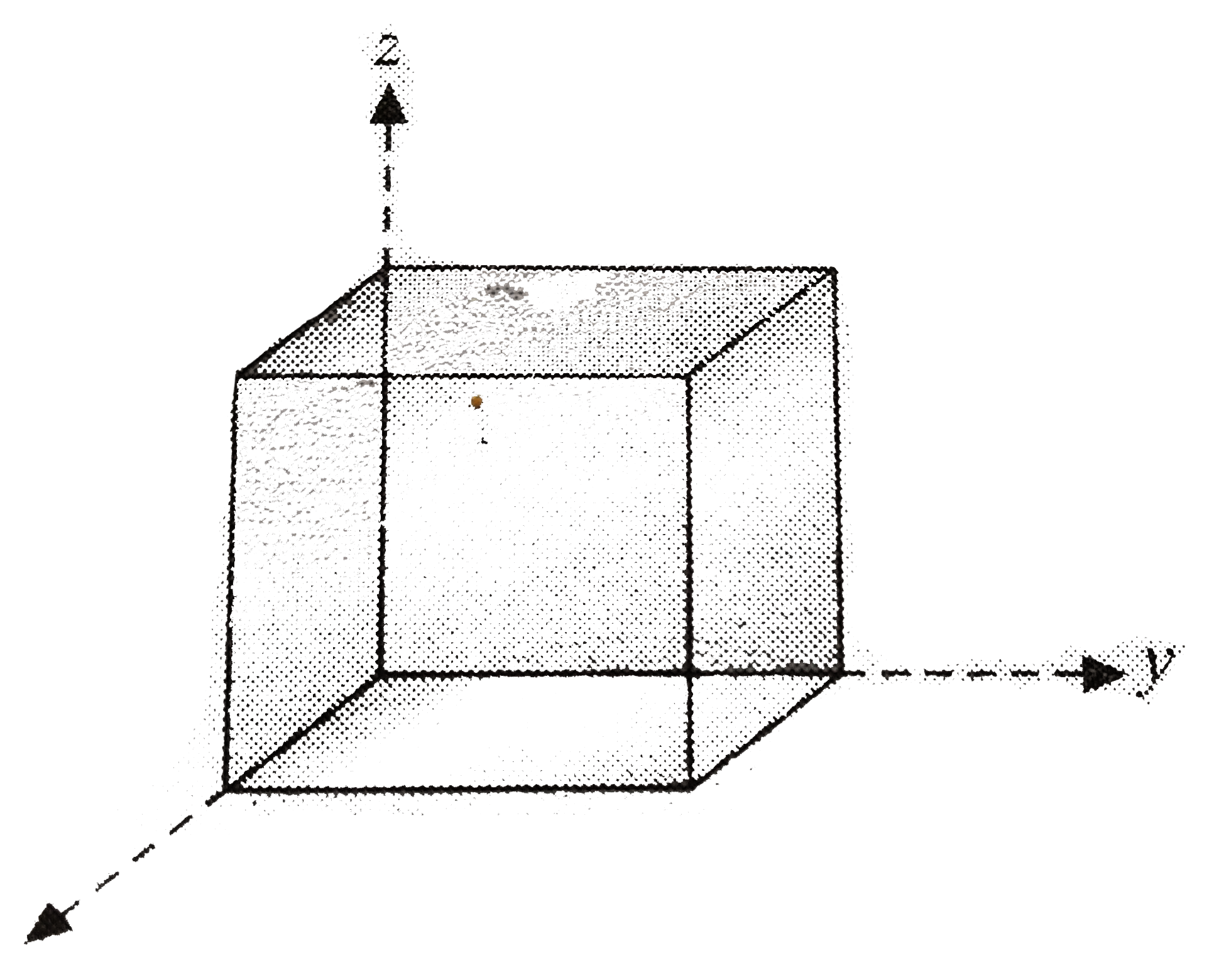
Each edge of the cube measures d, and one of the corners lies at the origin of the coordinates. Determine the net charge within the cube.View SolutionThe electric field in a cubical volume is
→E=E0(1+za)ˆi+E0(za)ˆj
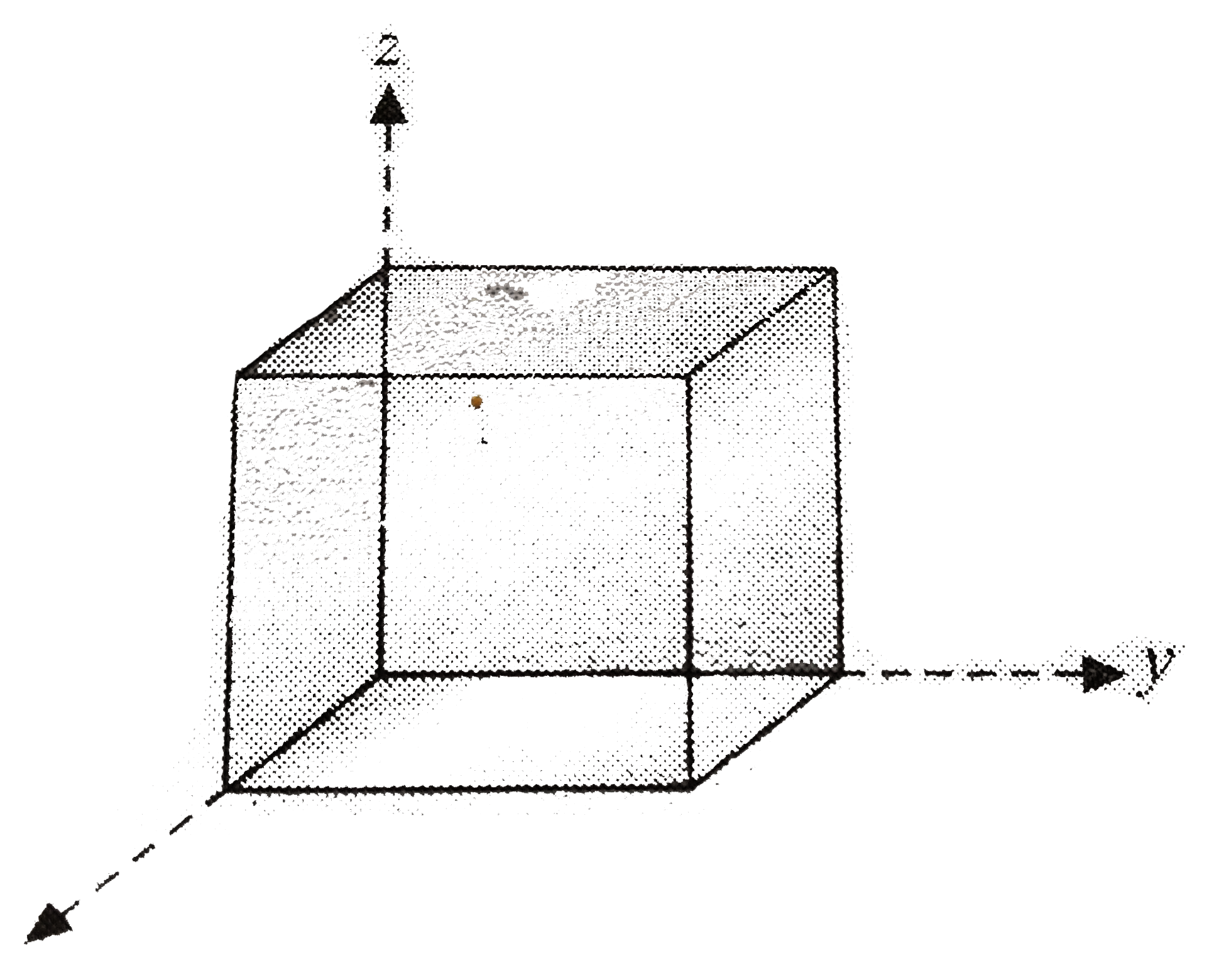
Each edge of the cube measures d, and one of the corners lies at the origin of the coordinates. Determine the net charge within the cube.View SolutionWhat will be the total flux throguh the faces of the cube, Fig with side of length a if a charge q is placed at (a) A : a corner of the cube (b) B : mid-point of an edge of the cube (c ) C : center of a face of the cube (d) D : mid-point of B and C.
View SolutionA point charge q is placed at the centre of a cube. What is the flux linked.
a with all the faces of the cube?
b. with each face of the cube?
c. if charge is not at the centre, then what will be the answer of parts a and b ?View SolutionA point charge q is placed at the centre of a cube. What is the flux linked.
a with all the faces of the cube?
b. with each face of the cube?
c. if charge is not at the centre, then what will be the answer of parts a and b ?View Solution

