At time t = 0 s, a disk is sliding on horizontal table with a velocity 3.00 m/s, 65.0∘ above the +x axis. As the disk slides, a constant acceleration acts on it that has the following components: ax=−0.460m/s2anday=−0.980m/s2. What is the velocity of the puck at time t = 1.50 s?
1.83 m/s, 62.0∘ above the +x axis
2.04 m/s, 71.3∘ above the +x axis
1.38 m/s, 65.2∘ above the +x axis
1.06 m/s, 58.7∘ above the +x axis
The correct Answer is:C
To find the velocity of the disk at time t=1.50s, we will follow these steps:
Step 1: Determine the initial velocity components
The initial velocity →u is given as 3.00m/s at an angle of 65∘ above the positive x-axis. We can break this velocity into its x and y components using trigonometric functions:
ux=ucos(θ)=3.00cos(65∘)
uy=usin(θ)=3.00sin(65∘)
Calculating these values:
ux=3.00cos(65∘)≈3.00×0.4226≈1.27m/s
uy=3.00sin(65∘)≈3.00×0.9063≈2.72m/s
Step 2: Identify the acceleration components
The acceleration components are given as:
ax=−0.460m/s2
ay=−0.980m/s2
Step 3: Calculate the final velocity components at t=1.50s
Using the first equation of motion:
vx=ux+ax⋅t
vy=uy+ay⋅t
Substituting the values:
vx=1.27+(−0.460)⋅(1.50)=1.27−0.69≈0.58m/s
vy=2.72+(−0.980)⋅(1.50)=2.72−1.47≈1.25m/s
Step 4: Calculate the magnitude of the final velocity
The magnitude of the final velocity v can be found using the Pythagorean theorem:
v=√v2x+v2y
Substituting the values:
v=√(0.58)2+(1.25)2=√0.3364+1.5625=√1.8989≈1.38m/s
Step 5: Calculate the angle of the final velocity
The angle ϕ with respect to the positive x-axis can be calculated using the tangent function:
ϕ=tan−1(vyvx)
Substituting the values:
ϕ=tan−1(1.250.58)≈tan−1(2.16)≈65.0∘
Final Result
Thus, the velocity of the disk at time t=1.50s is approximately:
Velocity≈1.38m/sat65.0∘above the positive x-axis
The initial velocity →u is given as 3.00m/s at an angle of 65∘ above the positive x-axis. We can break this velocity into its x and y components using trigonometric functions:
uy=usin(θ)=3.00sin(65∘)
ux=3.00cos(65∘)≈3.00×0.4226≈1.27m/s
uy=3.00sin(65∘)≈3.00×0.9063≈2.72m/s
The acceleration components are given as:
ax=−0.460m/s2
ay=−0.980m/s2
Using the first equation of motion:
vx=ux+ax⋅t
vy=uy+ay⋅t
vx=1.27+(−0.460)⋅(1.50)=1.27−0.69≈0.58m/s
vy=2.72+(−0.980)⋅(1.50)=2.72−1.47≈1.25m/s
The magnitude of the final velocity v can be found using the Pythagorean theorem:
v=√v2x+v2y
Substituting the values:
v=√(0.58)2+(1.25)2=√0.3364+1.5625=√1.8989≈1.38m/s
The angle ϕ with respect to the positive x-axis can be calculated using the tangent function:
ϕ=tan−1(vyvx)
Substituting the values:
ϕ=tan−1(1.250.58)≈tan−1(2.16)≈65.0∘
Thus, the velocity of the disk at time t=1.50s is approximately:
Velocity≈1.38m/sat65.0∘above the positive x-axis
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)3videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (LINKED COMPREHENSION)14videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PROBLEMS50videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Integer Type )3videos
MOTION ALONG A STRAIGHT LINE
- BOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Practice Questions57videos
OSCILLATIONS
Similar Questions
A body is projected horizontally from the top of a tower with a velocity of 20m/s .After what time the vertical component of velocity is four times the horizontal component of velocity (g=10ms2)
View Solutionif a=3t2+2t, initial velocity is 5m/s. Find the velocity at t=4s. The motion is in straight line, a is acceleration in m/s2 and t is time in seconds.
View Solution
Knowledge Check
- Question 1 - Select One
At time t=0 s a car passes a point with velocity of 16m/s and thereafter slows down with acceleration a=−0.5tm/s2 ,where t is in seconds. It stops at the instant t=
A32sB16sC8.0sD4.0s - Question 2 - Select One
The velocity of a particle moving with constant acceleration at an instant t0 is 10m/s After 5 seconds of that instant the velocity of the particle is 20m/s. The velocity at 3 second before t0 is:-
A12B1C2D4 - Question 3 - Select One
Vx is the velocity of a particle of a particle moving along the x−axis as shown. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s?
 A−2.0mB+2.0mC+1.0mD−1.0m
A−2.0mB+2.0mC+1.0mD−1.0m
At t=0, the particle is at the origin and its velocity is 10m/s at an angle 37∘ with the x-axis. The particle moves in x−y plane with a constant acceleration of 1m/s2 along the y-axis. Find the magnitude and direction of the velocity after 2s.
View SolutionA motorbike starts from the origin and moves over an xy plane with acceleration components ax=6.0m/s2anday=−3.0m/s2. The initial velocity of the motorbike has components v0x=12.0m/sandv0y=18.0m/s. Find the velocity of the motorbike, in unt-vector notation, when it reaches its greatest y coordinate.
View SolutionStarting from the origin at time t=0 ,with initial velocity [5hat jms^(-1) ,a particle moves in the x -y plane with a constant acceleration of ( 10ˆi+4ˆj)m/s 2 ms^(-2).At time t ,its coordinates are (20m,y_(0)m are,respectively:
View SolutionA particle is moving along x-axis such that its velocity varies with time according to v=(3m/s2)t−(2m/s3)t2. Find the velocity at t = 1 s and average velocity of the particle for the interval t = 0 to t = 5 s.
View Solutionvx is the velocity of a particle moving along the x-axis as shown in the figure. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s ?
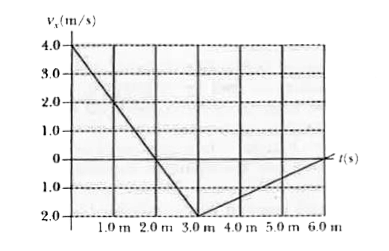 View Solution
View Solution

