Average velocity of the particle for the motion
3.3 m/s
6.7 m/s
2.7 m/s
7.6 m/s
The correct Answer is:A
Displacement Total area under the curve
Average velocity
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - GRB PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - More than one choice is correct
16 Videos
- MOTION IN A STRAIGHT LINEBOOK - GRB PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Assertion Reason
12 Videos
- MOTION IN A STRAIGHT LINEBOOK - GRB PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Problems and Practice
16 Videos
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Comprehension type
11 Videos
- MOTION IN TWO AND THREE DIMENSIONSBOOK - GRB PUBLICATIONCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - All Questions
210 Videos
Similar Questions
A particle moves rectilinearly with initial velocity u and constant acceleration a. Find the average velocity of the particle in a time interval from t=0 to t=t second of its motion.
View SolutionA particle moves rectilinearly with initial velocity u and constant acceleration a. Find the average velocity of the particle in a time interval from t=0 to t=t second of its motion.
View Solution
Knowledge Check
A particle is doing uniform circular motion as shown. Magnitude of average velocity of the particle between points A and C will be
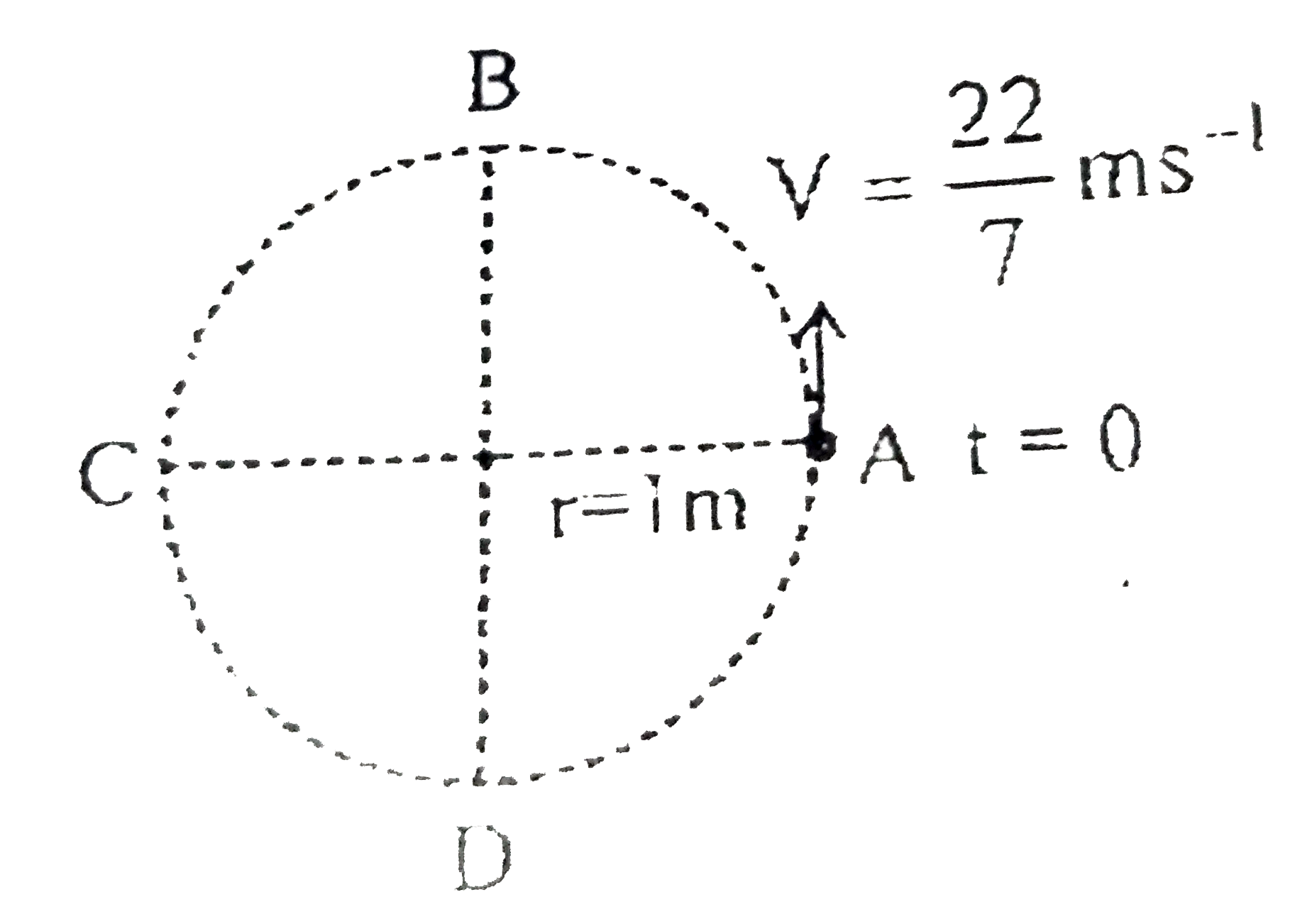 A2ms−1B25ms−1C25ms−1D13ms−1
A2ms−1B25ms−1C25ms−1D13ms−1A particle is projected with velocity v at an angle of θ with horizontal. The average angular velocity of the particle from the point of projection to impact equals:
AgcosθθvBgvsinθCgvθDgθvsinθVelocity time graph for the motion of a particle along a straight line is as shown in figure.

Average speed of the particle for the whole motion is:A9.6 m/sB7.2 m/sC8.3 m/sD6.5 m/s
Figure-1.20 shows displacement-time graphof a particle. Find the time during motion such that the average velocity of the particle during that period is zero.

View SolutionAverage velocity of a particle in projectile motion between its starting point and the highest point of its trajectory is (projectin speed = u, angle projection from horizontal =θ)
View SolutionAverage velocity of a particle in projectile motion between its starting point and the highest point of its trajectory is (projectin speed = u, angle projection from horizontal =θ)
View SolutionA particle retards from a velocity v0while moving in a straight line. If the magnitude of deceleration is directly proportional to the square loop of the speed of the particle, find its average velocity for the total time of its motion.
View SolutionAverage velocity of a particle in projectile motion between its starting point and the highest point of its trajectory is (projectin speed = u, angle projection from horizontal =θ)
View Solution
