Battery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance (Fig. 3.23). Determine the equivalent resistance of the network and the current along each edge of the cube.
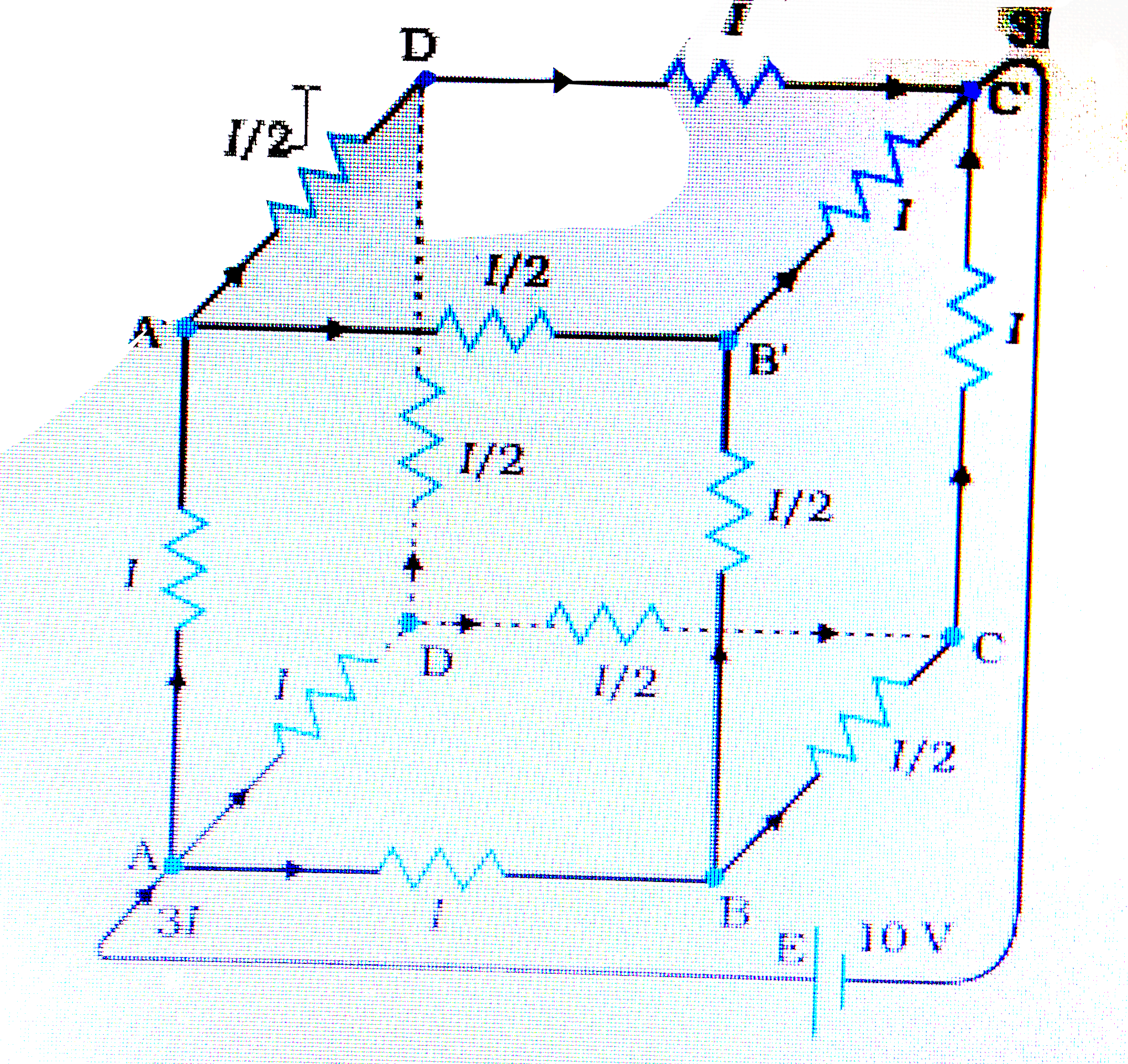
The network is not reducible to a simple series and parallel combinations of resistors. There is, however, a clear symmetry in the problem which we can exploit to obtain the equivalent resistance of the network. The paths are obviously symmetrically placed in the network. Thus, the current in each must be the same, say, . Further, at the corners , the incoming current must split equally into the two outgoing branches. In this manner, the current in all the 12 edges of the cube are easily written down in terms of , using Kirchhoff’s first rule and the symmetry in the problem. Next take a closed loop, say, ABCC'EA, and apply Kirchhoff’s second
rule:
where R is the resistance of each edge and the emf of battery. Thus,
The equivalent resistance of the network is
For for . the total current in the network is
i.e.,
The current flowing in each edge can now be read off from the fig.
Topper's Solved these Questions
Similar Questions
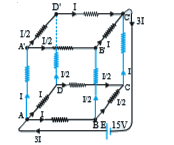
A battery of 15 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 5Ω . Determine the equivalent resistance of the network and the current along each edge of the cube.
View SolutionIn the adjoining network of resistors each is of resistance rΩ. Find the equivalent resistance between A and B.
View Solution
Knowledge Check
Five equal resistances each of value R are connected in a form shown alongside. The equivalent resistance of the network
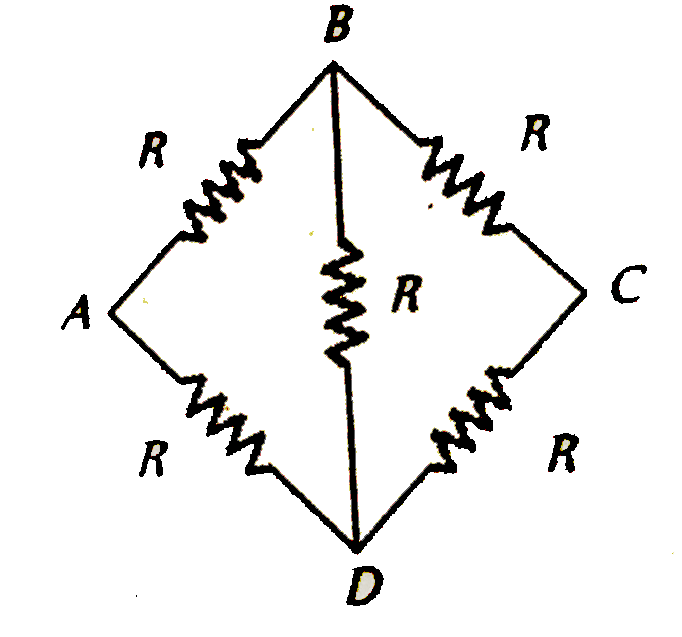 A12RB2RC58RD85R
A12RB2RC58RD85R
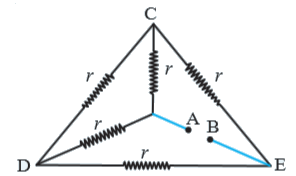
In the given network of resistors, each of resistance R, calculate the equivalent resistance between the junctions A and E

View SolutionA 10 V storage battery of negligible internal resistance is connected across a 50Ω resistor. How much heat energy is produced in the resistor in 1 hour
View SolutionIn the adjoining network of resistors, each is of resistance r ohm, the equivalent resistance between points A and B is–

View SolutionA network of resistors is connected to a 16V battery as shown in the following figure. Compute the equivalent resistance of the network.
View SolutionA 5 V battery of negligible internal resistance is connected across a 200 V battery and a resistance of 39Ω as shown in the figure. Find the value of the current.

View SolutionFour equal resistors, each of resistance 10Ω, are connected as shown in the circuit diagram. The equivalent resistance between A and B is
View SolutionFive equal resistance each of value R are connected in a circuit . Find equivalent resistance of the network between points A and C
View Solution
