Bob B of the pendulum AB is given an initial velocity √3Lg in horizontal direction. Final the maximum height of the bob from the starting point,
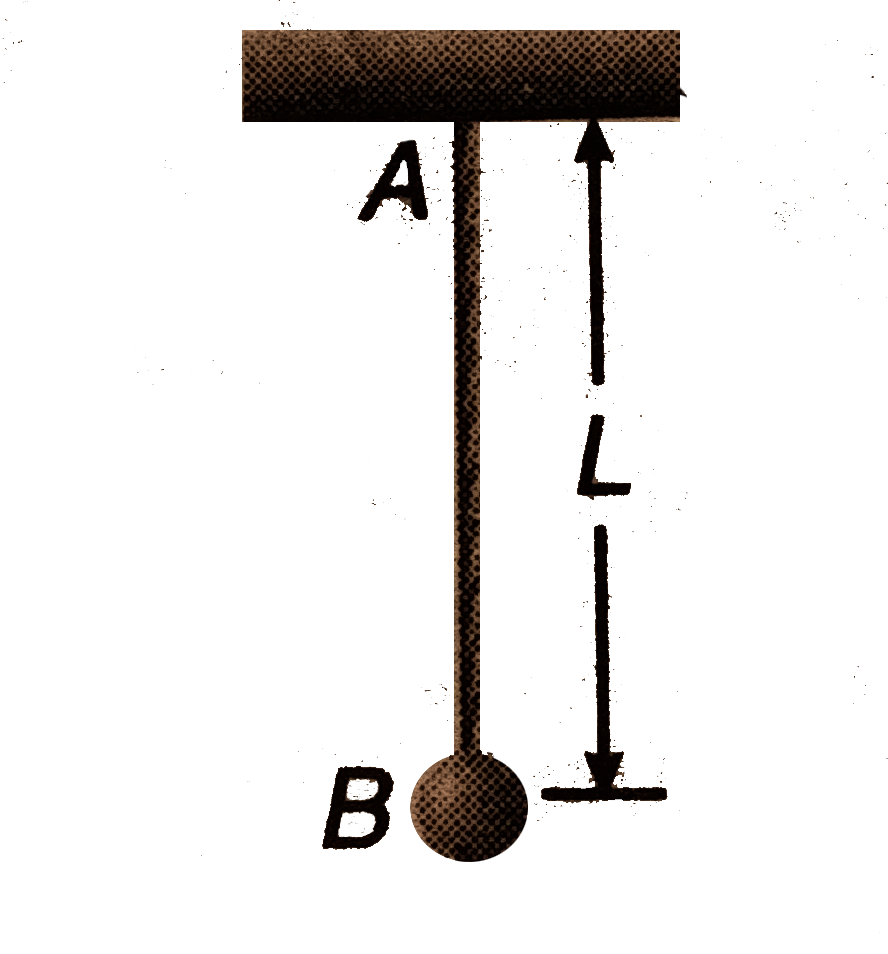
(a) if AB is a massless rod,
(b) if AB is a massless staring.
The correct Answer is:A, B, C, D
Applying conservation of energy
mgh=12m(√3Lg)2
oh=3L2
(b) Since, √3Lg lies between √2Lg and √5Lg , the stringt will slack in upper half of the circle. Assuming that string slack when it makes an angle θ with horizontal. We have
mgsinθ=mv2L ...(i)
v2=(√3gL2)−2gL(1+sinθ) ...(ii)
Solving Eq. (i) and Eq. (ii) , we get
sinθ=13
and v2=gL3
Maximum height of the bob from starting point,
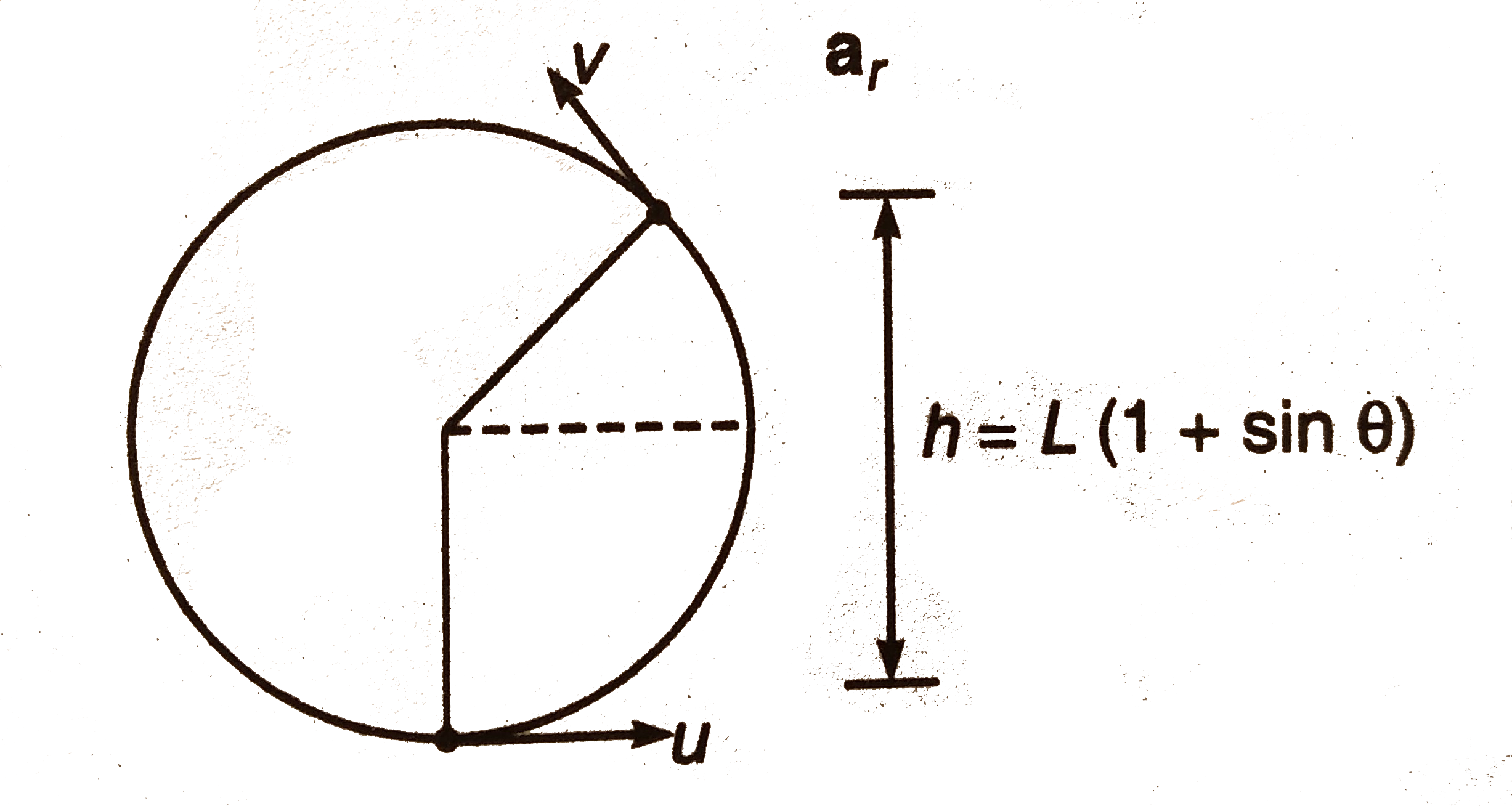
H=L(1+sinθ)+v2sin2(90∘−θ)2g
=4L3+(gL6g)cos2θ4L3+4L27
=4027L
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Subjective Questions2videos
CIRCULAR MOTION
- BOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - JEE Main23videos
CIRCULAR MOTION
- BOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 Comprehension Based5videos
CIRCULAR MOTION
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective21videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct27videos
COMMUNICATION SYSTEM
Similar Questions
The bob of pendulum is project with horizontal velocity of √3gf I is the length of string. Find the angular displacement of string before it becomes slack.
 View Solution
View SolutionThe bob of a stationary pendulum is given a sharp hit to impart it a horizontal speed of √3gl. Find the angle rotated by the string before it becomes slack.
View Solution
Knowledge Check
- Question 1 - Select One
If 'V' be the maximum velocity of the bob of a pendulum and 'h' the maximum height of the bob from its point of rest, then
AV=2ghBV=√hgCV=√2ghDV=gh - Question 2 - Select One
A small bob mass 'm' is suspended by a massless string from a cart of the same mass 'm' as shown in the figure. The friction between the cart and horizontal ground is negligible. The bob is given a velocity V0 in horizontal direction as shown. The maximum height attained by the bob is , ( initially whole system ( bob + string + cart ) was at rest ).
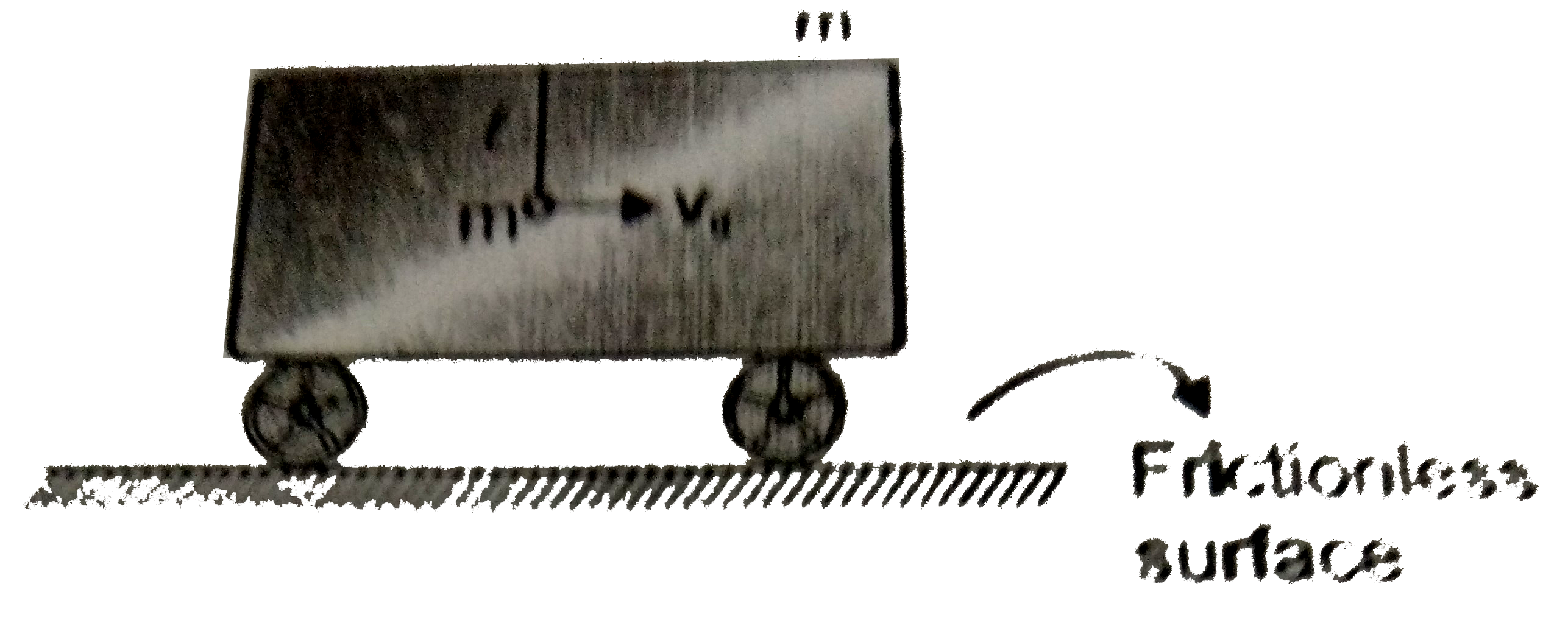 A2V20gBV20gCV204gDV202g
A2V20gBV20gCV204gDV202g - Question 3 - Select One
The length of a simple pendulum is 1m. The bob is given a velocity 7ms−1 in horizontal direction from mean position. During upward motion of bob, if the string breaks when the bob is horizontal, then the maximum vertical height of ascent of bob from rest position is
A2.5mB2 mC3 mD3.5m
The bob of a pendulum at rest is given a sharp hit to impat a horizontal velocity √10gl where l is the length of the pendulum. Find the tension in the string when a. the string is horizontal. B. The bob is at its highest point and c. the string makes an angle of 600 with teh upward vertical.
View SolutionBob of the pendulum is at its bottom most point when it is given horizontal velocity √57 m/s . Length of the string is 1.5 m .
(i) Find maximum height attained by the bob above its lowest point .
(b) What will be the answer to part (a) if intial velocity given s √95 m/s ?View SolutionIn th efigure shown in fig. 10.33 , a bob attached with a light string of radius R is given as initial velocity u=√4gR at the bottommost point.
(a) At what height string will slack.
(b) What is velocity of the bob just befare slacking of string.
 View Solution
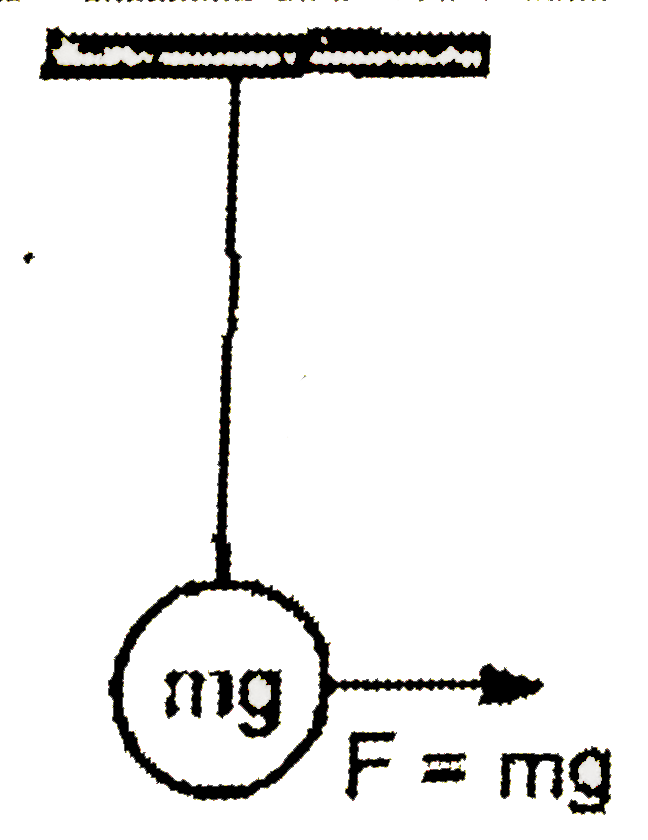
View SolutionA pendulum bob of mass m is suspended at rest. A constant horizontal force F=mg starts acting on it. Find
(a) the maximum angular defection of the string.
(b) the maximum possible tension in the string.
 View Solution
View SolutionBob of a simple pendulum of length L is projected horizontally with a speed of u=√4gh, , from the lowest position. Find the distance of the bob from vertical line AB, at the moment its tangential acceleration becomes zero.
 View Solution
View Solution

