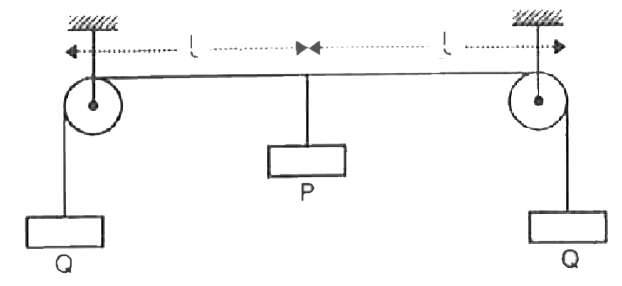
Calculate of velocity $v$ of the falling masss P after it has gone down by $x$ in an axle and wheel system of radii r and R respectively (Figure 2.12)

[Hint : Let Q go up by $y$ when P down by x
Then $\frac{x}{y} = \frac{R}{r} ∴ x = \frac{R}{r} y$
Apply work-energy theorem to the system (P+Q+ceiling). Remember that the gravitational pulls are the lone forces external to the system, the tensions and pull of ceiling are internal forces of the system]

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $\sqrt{2 g x (P - \frac{r}{R} Q) / (P + \frac{r^{2}}{R^{2}} Q)}$

Answer

Step by step video, text & image solution for Calculate of velocity v of the falling masss P after it has gone down by x in an axle and wheel system of radii r and R respectively (Figure 2.12) [Hint : Let Q go up by y when P down by x Then (x)/(y)=(R)/(r) :. x=(R)/(r)y Apply work-energy theorem to the system (P+Q+ceiling). Remember that the gravitational pulls are the lone forces external to the system, the tensions and pull of ceiling are internal forces of the system] by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 PHYSICS WORK, ENERGY AND POWER

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
Let $p, q, r ε R$ be such that $2 q = p + r$ and $\frac{2017 - x}{p x} = \frac{2017 - y}{q y} = \frac{2017 - z}{r z}$ , then the correct relation between x,y,z is
A $\frac{x}{x} = \frac{x - y}{y - z}$
B $\frac{x}{y} = \frac{x - y}{y - z}$
C $\frac{x}{z} = \frac{x - y}{y - z}$
D $\frac{x + z}{y + z} = \frac{x - z}{y - z}$
Question 2 - Select One
If $(q + r) x + (r + p) y + (p + q) z = k$
and $(q - r) x + (r - p) y + (p - q) z = k$
represent the equation of a line then the equation of the line through origin and parallel to given lines is :
A $\frac{x}{q^{2} - r^{2}} = \frac{y}{r^{2} - p^{2}} = \frac{z}{p^{2} - q^{2}}$
B $\frac{x}{p^{2} - q r} = \frac{y}{q^{2} - p r} = \frac{z}{r^{2} - p q}$
C $\frac{x}{q} = \frac{y}{r} = \frac{z}{p}$
Dnone
Question 3 - Select One
For the real numbers p, q, r, x, y, let $p < x < q$ and $p < y < r$ . Which one of the following is correct ?
A $p x < x y < r$
B $p < x < q < r$
C $p < y < x < q$
DNone of these

NN GHOSH-FRICTION, WORK POWER AND ENERGY-Exercises (B)

Home
Ask Doubt
Profile

The correct Answer is:√2gx(P−rRQ)/(P+r2R2Q)

Topper's Solved these Questions

Similar Questions

Knowledge Check

Let p,q,rεR be such that 2q=p+r and 2017−xpx=2017−yqy=2017−zrz , then the correct relation between x,y,z is

If(q+r)x+(r+p)y+(p+q)z=k and(q−r)x+(r−p)y+(p−q)z=k represent the equation of a line then the equation of the line through origin and parallel to given lines is :

For the real numbers p, q, r, x, y, let p<x<q and p<y<r. Which one of the following is correct ?

NN GHOSH-FRICTION, WORK POWER AND ENERGY-Exercises (B)

The correct Answer is: $\sqrt{2 g x (P - \frac{r}{R} Q) / (P + \frac{r^{2}}{R^{2}} Q)}$

Let $p, q, r ε R$ be such that $2 q = p + r$ and $\frac{2017 - x}{p x} = \frac{2017 - y}{q y} = \frac{2017 - z}{r z}$ , then the correct relation between x,y,z is

If $(q + r) x + (r + p) y + (p + q) z = k$
and $(q - r) x + (r - p) y + (p - q) z = k$
represent the equation of a line then the equation of the line through origin and parallel to given lines is :

For the real numbers p, q, r, x, y, let $p < x < q$ and $p < y < r$ . Which one of the following is correct ?