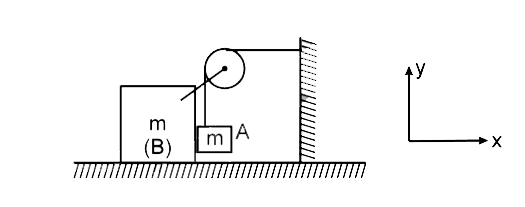
If the system if Figure 7.13 is released from rest in the configuration shown by solid lines, find the maximum distance h through which the weight will fall. (Neglect friction and masses of pulleys) What will happen if P=2Q ?
![If the system if Figure 7.13 is released from rest in the configuration shown by solid lines, find the maximum distance h through which the weight will fall. (Neglect friction and masses of pulleys) What will happen if P = 2Q ? [Hint : Apply work-energy theorem to the compound system consisting of the three masses and ceiling. To find intantaneous velocities of the masses apply the condition that the length of the string remains constant. Also remember that gravitational pulls are the lone forces external to the system, the tension of the string and pull the internal force ceiling are of the system]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/NEP_NGM_PHY_GP_C07_E01_021_Q01.png)
[Hint : Apply work-energy theorem to the compound system consisting of the three masses and ceiling. To find intantaneous velocities of the masses apply the condition that the length of the string remains constant. Also remember that gravitational pulls are the lone forces external to the system, the tension of the string and pull the internal force ceiling are of the system]
The correct Answer is:h=4PQl/(4Q2−P2). The system will acquire terminal velocity =√gl
Topper's Solved these Questions
- FRICTION, WORK POWER AND ENERGYBOOK - NN GHOSHCHAPTER - FRICTION, WORK POWER AND ENERGYEXERCISE - Exercises (A)
15 Videos
- FIRST LAW OF THERMODYNAMICSBOOK - NN GHOSHCHAPTER - FIRST LAW OF THERMODYNAMICSEXERCISE - All Questions
39 Videos
- GRAVITATIONBOOK - NN GHOSHCHAPTER - GRAVITATIONEXERCISE - EXERCISE
29 Videos
Similar Questions
Knowledge Check
In the figure shown neglecting friction and mass of pulley, what is the acceleration of mass B ?
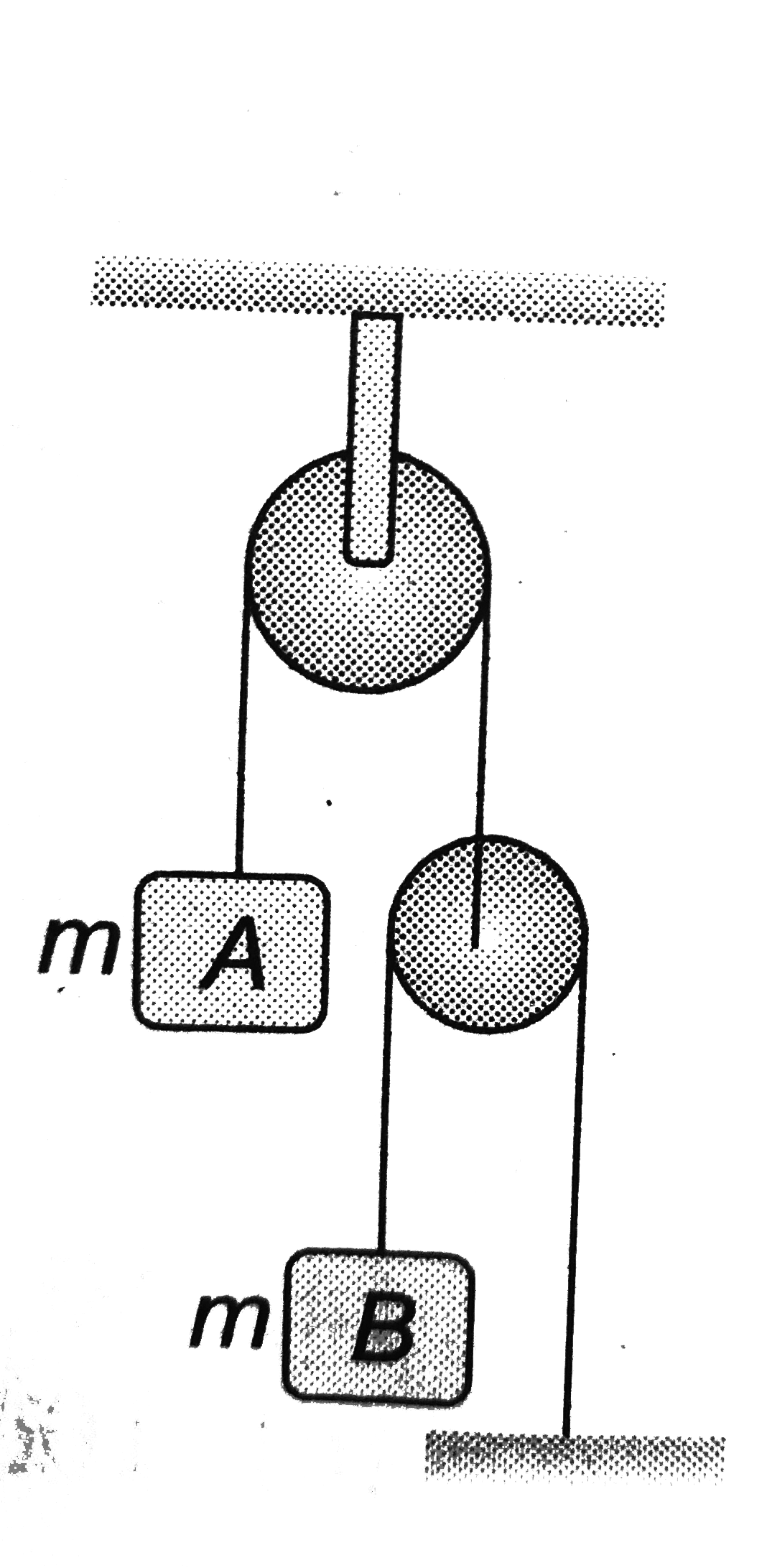 Ag3B5g2C2g2D2g5
Ag3B5g2C2g2D2g5The system shown in the figure is released from rest. At the instant when mass M has fallen through a distance h, the velocity of m will be
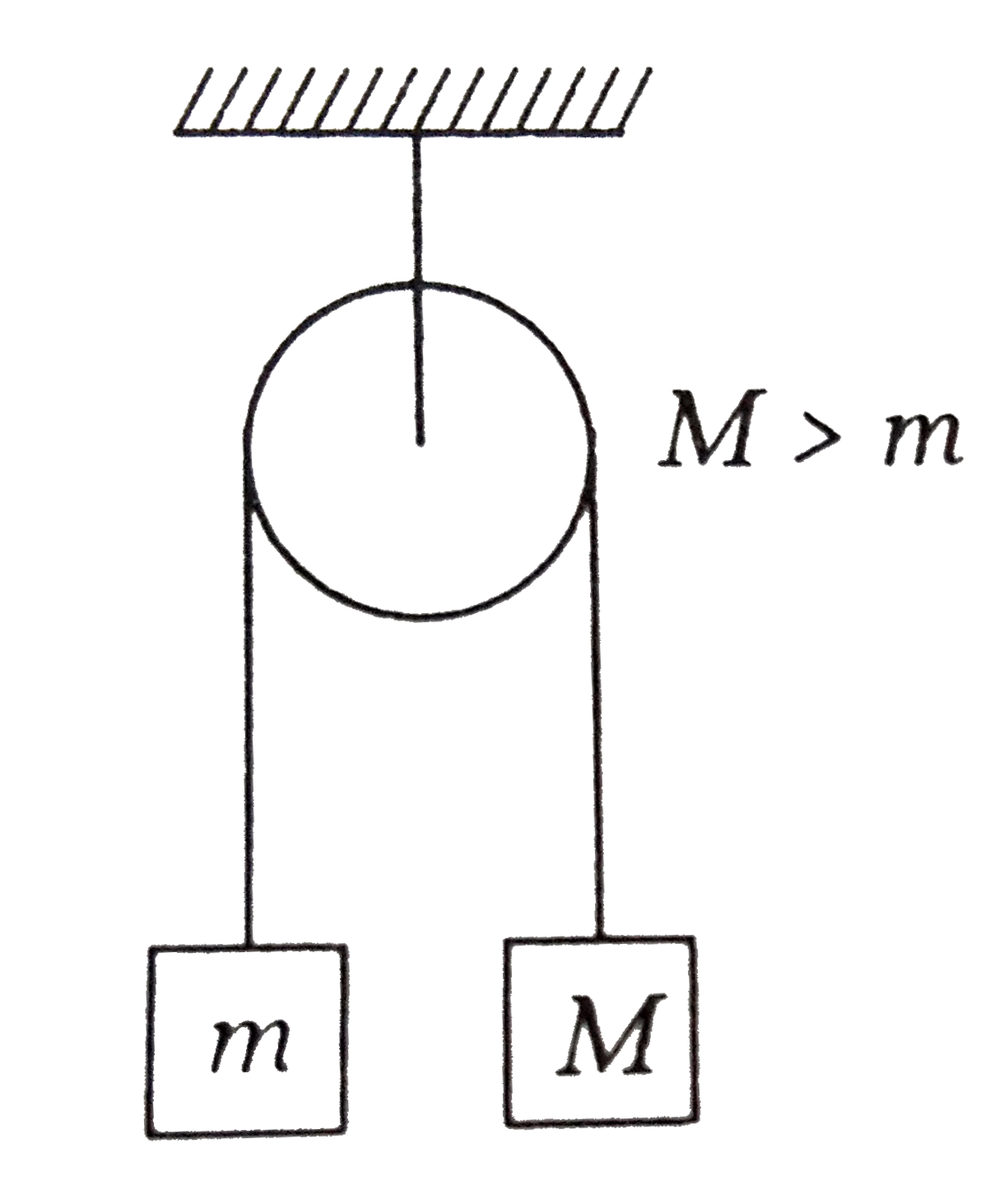 A√2ghB√2ghMmC√2gh(M−m)m+MD√2gh(M+m)m−M
A√2ghB√2ghMmC√2gh(M−m)m+MD√2gh(M+m)m−M
The system shown in the figure is released from rest. At the instant when mass M has fallen through a distance h, the velocity of m will be

View SolutionFind the velocity of center of mass of the system shown in the figure.

View SolutionFind the velocity of center of mass of the system shown in the figure.

View SolutionFind the velocity of the center of mass of the system shown in the figure .

View SolutionIn the system shown, the masses are released from rest. What shall be the acceleration of the moving masses?
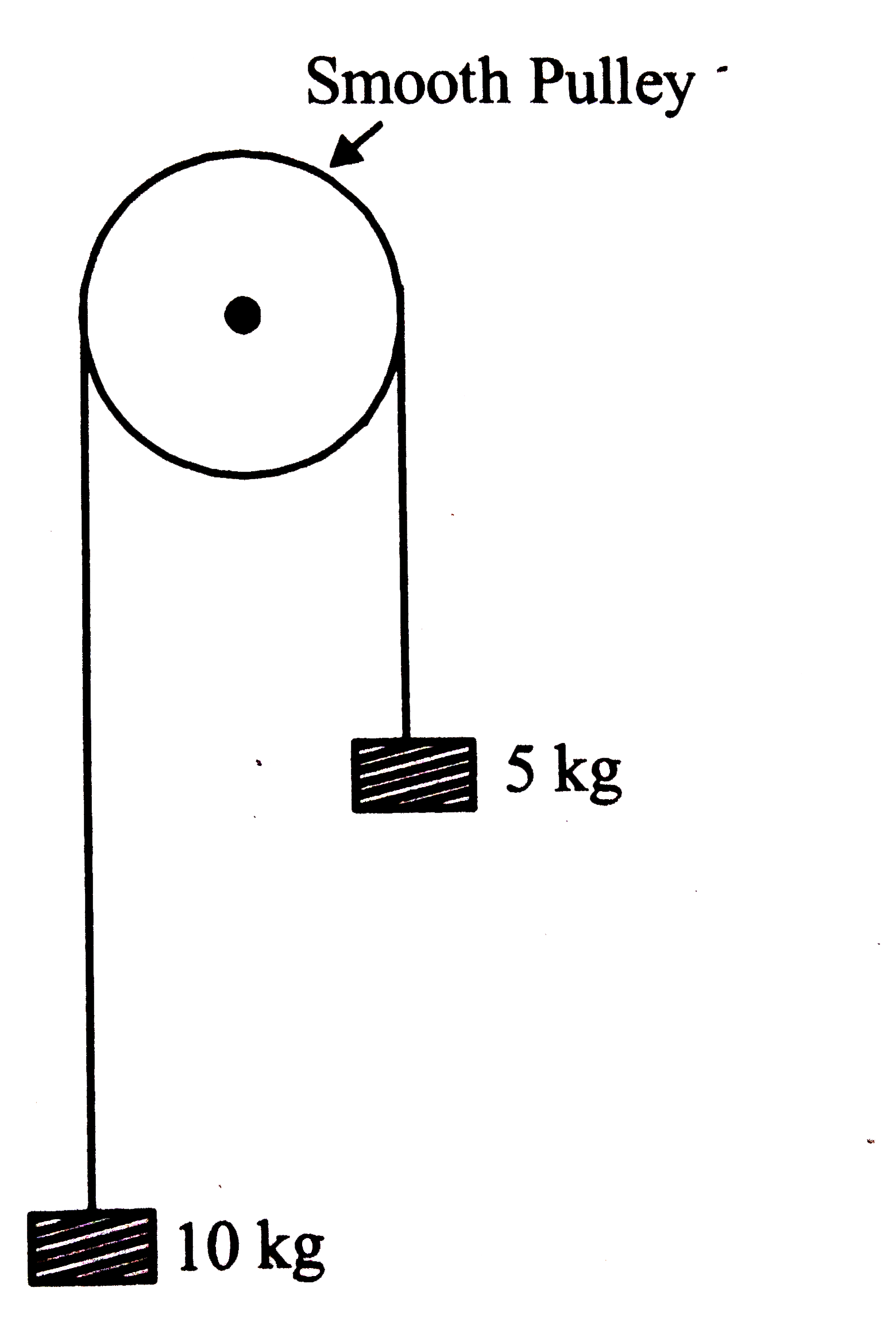
View SolutionCalculate of velocity v of the falling masss P after it has gone down by x in an axle and wheel system of radii r and R respectively (Figure 2.12)
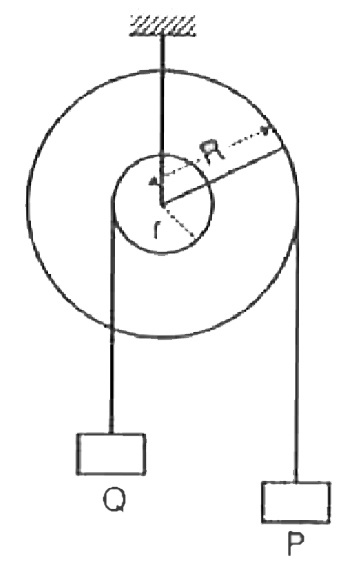
[Hint : Let Q go up by y when P down by x
Then xy=Rr∴x=Rry
Apply work-energy theorem to the system (P+Q+ceiling). Remember that the gravitational pulls are the lone forces external to the system, the tensions and pull of ceiling are internal forces of the system]
View Solution