Calculate the kinetic energy of a hollow metal sphere of mass 2 kg, which rolls over a horizontal surface with a linear velocity of 20 cm/s ?
To calculate the kinetic energy of a hollow metal sphere that rolls over a horizontal surface, we need to consider both its translational and rotational kinetic energy. Here’s a step-by-step solution:
Step 1: Identify the formulas for kinetic energy
The total kinetic energy (KE) of a rolling object is the sum of its translational kinetic energy (KEt) and rotational kinetic energy (KEr):
KE=KEt+KEr
Where:
- KEt=12mv2 (translational kinetic energy)
- KEr=12Iω2 (rotational kinetic energy)
Step 2: Determine the moment of inertia for a hollow sphere
The moment of inertia I for a hollow sphere is given by:
I=23mR2
Where m is the mass and R is the radius of the sphere.
Step 3: Relate angular velocity and linear velocity
For a sphere rolling without slipping, the relationship between linear velocity v and angular velocity ω is:
v=Rω⇒ω=vR
Step 4: Substitute ω into the rotational kinetic energy formula
Substituting ω into the rotational kinetic energy formula gives:
KEr=12Iω2=12(23mR2)(vR)2
Simplifying this:
KEr=12(23mR2)(v2R2)=13mv2
Step 5: Combine translational and rotational kinetic energy
Now, we can express the total kinetic energy:
KE=KEt+KEr=12mv2+13mv2
Finding a common denominator (which is 6):
KE=36mv2+26mv2=56mv2
Step 6: Substitute the values of mass and velocity
Given:
- Mass m=2kg
- Velocity v=20cm/s=0.2m/s
Now substituting these values into the total kinetic energy formula:
KE=56×2kg×(0.2m/s)2
Calculating:
KE=56×2×0.04=5×0.086=0.46=0.06667J
Final Answer
The total kinetic energy of the hollow metal sphere is approximately:
KE≈0.067J
---
The total kinetic energy (KE) of a rolling object is the sum of its translational kinetic energy (KEt) and rotational kinetic energy (KEr):
KE=KEt+KEr
Where:
- KEt=12mv2 (translational kinetic energy)
- KEr=12Iω2 (rotational kinetic energy)
The moment of inertia I for a hollow sphere is given by:
I=23mR2
Where m is the mass and R is the radius of the sphere.
For a sphere rolling without slipping, the relationship between linear velocity v and angular velocity ω is:
v=Rω⇒ω=vR
Substituting ω into the rotational kinetic energy formula gives:
KEr=12Iω2=12(23mR2)(vR)2
Simplifying this:
KEr=12(23mR2)(v2R2)=13mv2
Now, we can express the total kinetic energy:
KE=KEt+KEr=12mv2+13mv2
Finding a common denominator (which is 6):
KE=36mv2+26mv2=56mv2
Given:
- Mass m=2kg
- Velocity v=20cm/s=0.2m/s
KE=56×2kg×(0.2m/s)2
Calculating:
KE=56×2×0.04=5×0.086=0.46=0.06667J
The total kinetic energy of the hollow metal sphere is approximately:
KE≈0.067J
Topper's Solved these Questions
Similar Questions
Calculate the kinetic energy of a solid sphere of mass 2kg rolling down an inclined plane with a velocity of 2m/s about an axis passing through its diameter.
View SolutionCalculate the kinetic energy of a solid sphere of mass 2kg rolling down an inclined plane with a velocity of 2m/s about an axis passing through its diameter.
View SolutionCalculate the kinetic energy of a body of mass 2 kg moving with speed of 10 m s−1
View SolutionCalculate the kinetic energy of a body of mass 0.1 kg and momentum 20 kg ms−1
View SolutionA uniform rod AB of mass M and length √2R is moving in a veritcal plane inside a hollow sphere of radius R. The sphere is rolling on a fixed horizontal surface without slipping with velocity of its centre of mass 2v. When the end B is the lowest position, its speed is found to be v as shown in the figure. If the kinetic energy of the rod at this instant is 4KMv2. Find K.
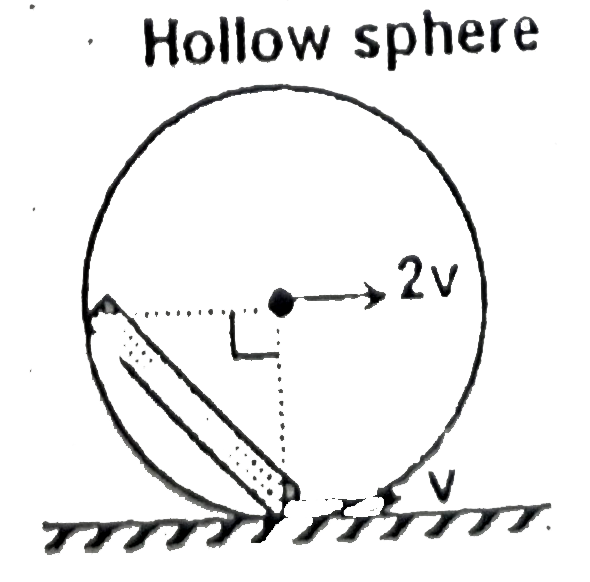
View SolutionA uniform thin ring of mass 0.4kg rolls without slipping on a horizontal surface with a linear velocity of 10 cm/s. The kinetic energy of the ring is
View SolutionA uniform hollow sphere of mass 200 g rolls without slipping on a plane horizontal surface with its centre moving at a speed of 5.00 cm/s. Its kinetic energy is:
View SolutionA uniform hollow sphere of mass 200 g rolls without slipping on a plane horizontal surface with its centre moving at a speed of 5.00 cm/s. Its kinetic energy is:
View SolutionA uniform hollow sphere of mass 400 g rolls without slipping on a plane horizontal surface with its centre moving at a speed of 10 cm/s. Its kinetic energy is:
View SolutionA uniform hollow sphere of mass 400 g rolls without slipping on a plane horizontal surface with its centre moving at a speed of 10 cm/s. Its kinetic energy is:
View Solution
