Calculate the magnetic induction at a point on the axial line of a bar magnet.Solution in Tamil
Magnetic field at a point along the axial line of the magnetic dipole (bar magnet):
Consider a bar magnet NS. Let N be the North Pole and S be the south pole of the bar magnet, each of pole strength qm and separated by a distance of 2l. The magnetic field at a point C (lies along the axis of the magnet) at a distance from the geometrical center O of the bar magnet can be computed by keeping unit north pole (qMC= 1 Am) at C. The force experienced by the unit north pole at C due to pole strength can be computed using Coulomb.s law of magnetism as follows:
The force of repulsion between north of the bar magnet and unit north pole at point C (in free space) is →FN=μ04πqm(r−1)ˆi............(1)
where r-l is the distance between north pole of the bar magnet and unit north pole at C.
The force of altration between South Pole of the bar magnet and unit North Pole at point C (in free space) is veFSqm(r+l)2ˆl...........(2)
where r+1 is the distance between south pole of the bar magnet and unit north pole at C.
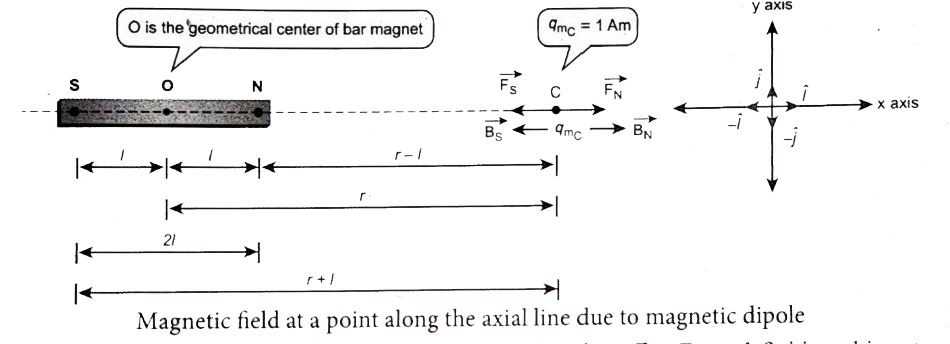
From equation (1) and (2), the net force at point C is →F=→FN+→FS. From definition, this net force is the magnetic field due ot magnetic dipole at a point C(→F=→B)
→B=μ04π(r−l)2ˆi+(μ04πqm(4+l)2ˆi)=μ0qm4π(1(r−l)2−1(r+l)2)ˆi⇒→B=μ02r4π(qm.(2l)(r2−l2)2)ˆi..........(3)
Since, magnitude of magnetic dipole moment is |→pm|=pm=qm.2l the magnetic field point C equation (3) can be written as
→Baxial=μ04π(2rpm(r2−l2)2)ˆi...........(4)
If the distace between two poles in a bar magnetic are small (looks like short magnet) compared to the distance geometrical centre O of hte bar magnet and the location of point C i.e,
r>>1 then (r2−l2)2≈r4.............(5)
Therefore, using equation (5) in equation (4), we get
→Baxial=μ04π(2rpmr3)ˆi=μ04π2r3→pm
Where →pm=pmˆi.............(6)
Topper's Solved these Questions
Similar Questions
Write down Coulomb 's law in vector form and mention what each term represents .
View SolutionDerive an expression for electrostatic potential energy of the dipole in a uniform electric field .
View SolutionDefine capacitance . Give its unit.
View SolutionThe magnetic induction field strength at a distance 0.3m on the axial line of a short bar magnet of moment 3.6Am2 is
View SolutionMagnetic inducton at a point on the axial line of a short bar magnet is B towards east. If the magnet is turned through 90^(0) in clock wise direction, then magnetic induction at the same point is (Neglect earth's magnetic field)
View SolutionThe magnetic induction field strength at a distance 0.2 m on the axial line of a short bar magnet of mement 3.6Am^(2) is
View SolutionDefine axial line of a bar magnet.
View SolutionThe magnetic induction due to a bar magnet at an axial point is directed along the axis
View SolutionThe magnetic induction due to a bar magnet at an axial point is directed along the axis
View SolutionCalculate the magnetic induction at a point on the axial line of a bar magnet.
View SolutionWhat is the magnetic field along the axis and equatorial line of a bar magnet ?
View SolutionWhat is the magnetic field along the axis and equatorial line of a bar magnet ?
View SolutionWhat is the magnetic field along the axis and equatorial line of a bar magnet ?
View SolutionWhat is the magnetic field along the axis and equatorial line of a bar magnet ?
View SolutionWhat is the magnetic field along the axis and equatorial line of a bar magnet ?
View Solution
