Calculating the magnetic moment ( in Am2) of a thin wire with a current I=0.8A, wound tightlly on a half a tore (see figure). The diameter of the cross section of the tore is equal to d=5cm, and the number of turns is N=500.
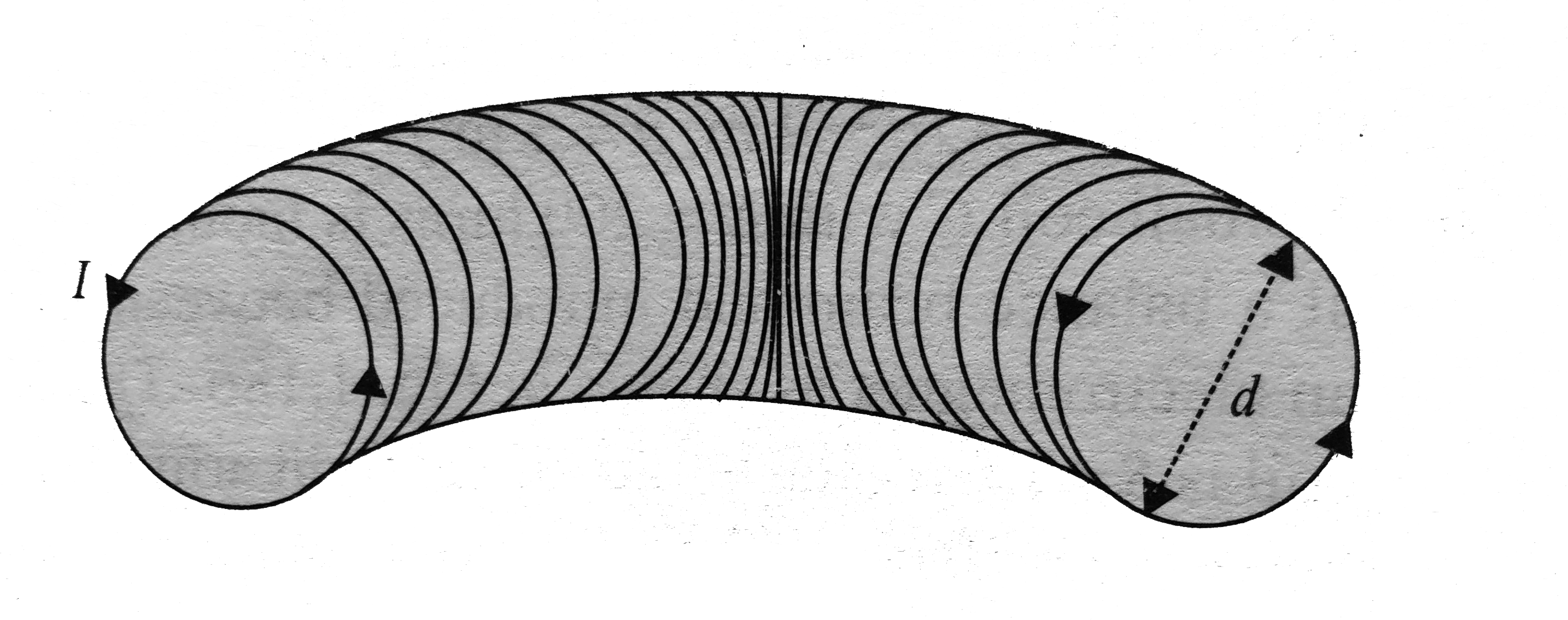
The correct Answer is:5
The magnetic moment of circular current is given by AI, I being
the curculating current and A is the area of cross-section, the
direction is perpendicular to the plane of current. Now, for an
element of toroid of length rdq, its magnetic moment is along the
direction of arrow as shown, of magnitude (perpendicular to its
cross-section)=currentxareaxnumber of turns in the length rdq.

dM=Iπd24(Nπrrdθ)=N4d2Idθ
Resolving dM into components along x and y, we get dMsinθ
and dMcosθ, components along y form neightbouring elements
cancel out to zero, and components along x are added. so
M=∫dMsinθ=∫π0N4,d2Isinθdθ=Nd2I2
putting the given values we get M=5Am2.
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Archives Fill In The Blank
6 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Archives True /false
4 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Linked Comprehension
28 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
Similar Questions
Calculating the magnetic moment ( in Am2) of a thin wire with a current I=8A, wound tightlly on a half a tore (see figure). The diameter of the cross section of the tore is equal to d=5cm, and the number of turns is N=500.

View SolutionA small coil is introduced between the poles of an electromagnet so that its axis coincides with the magnetic field direction. The cross-sectional area of the coil is equal to S=3.0mm2, the number of turns is N=60. When the coil turns through 180∘ about its diameter, a galvanometer connected to the coil indicates a charge q=4.5μC flowing through it. Find the magnetic induction magnitude between the poles, provided the total resistance of the electric circuit equals R=40Ω.
View Solution
Knowledge Check
A long straight cable of length l is placed symmetrically along z-axis and has radius a(<<l). The cable consists of a thin wire and a co- axial conducting tube. An alternating current I(t)=I0 sin (2πvt). Flows down the central thin wire and returns along the co-axial conducting tube. the induced electric at a distance s from the wire inside the cable is
E(s,t)=μ0I0v cos (2πvt)In(sa)ˆk.
(i) Calculate the displacement current density inside the cable.
(ii) Integrate the displacement current density across the cross- section of the cable to find the total displacement current Id.
(iii) compare the conduction current I0 with the displacement current Id0.A2πλ2I0ln(as)sin(2πυt)ˆkB1λ2I0ln(as)sin(2πυt)ˆkCπλ2I0ln(as)sin(2πυt)ˆkDZero
Find the magnetic induction of the field at the point O at a loop with current I, whose shape is illustrated in figure
(a)In figure a the radii a and b, as well as the angle φ are known
(b)In figure b,the raidus a and the side b are known.
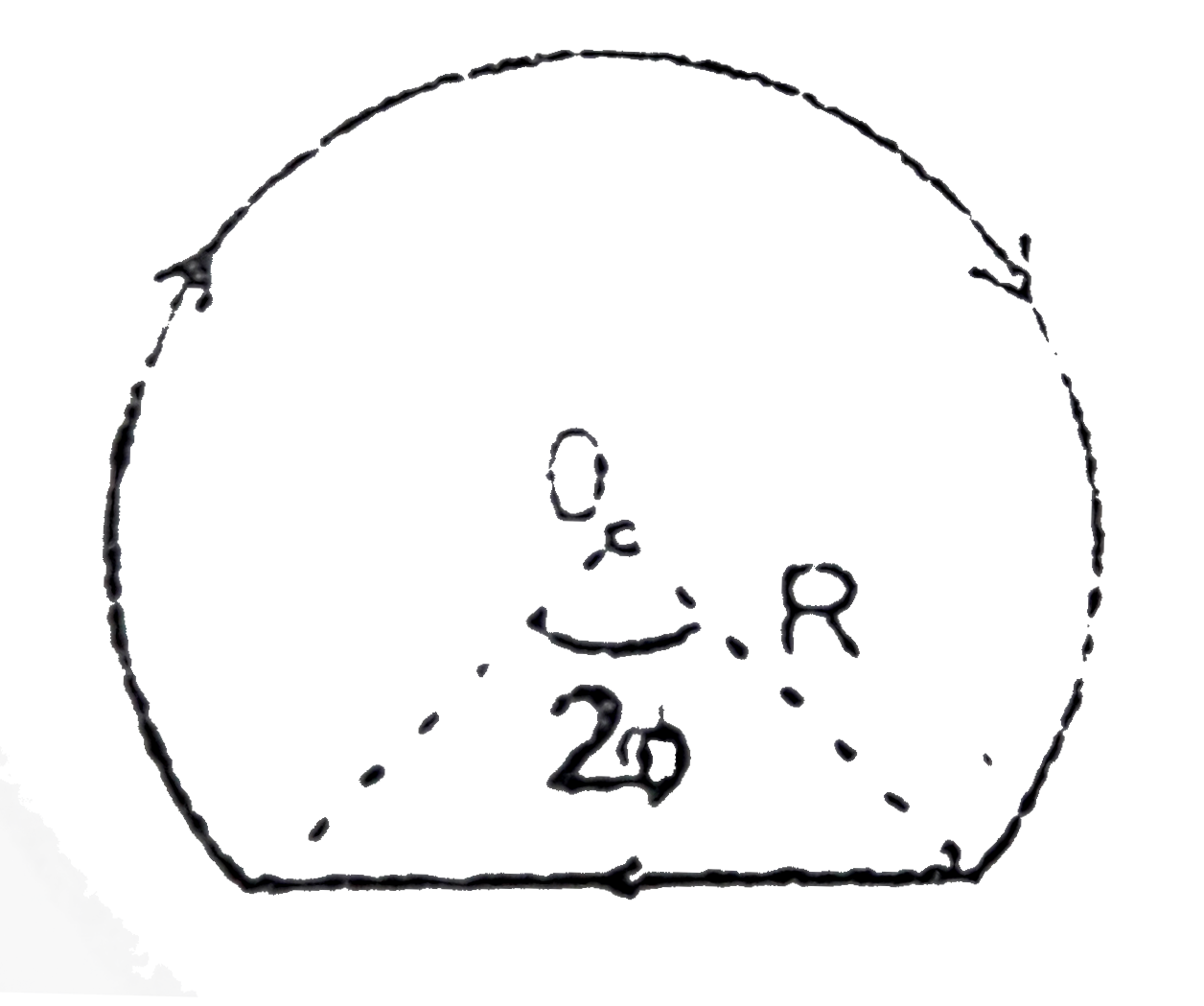
(c)A current I=5.0A flows along a thin wire shaped as shown in figure.The radius of a curved part of the wire is equal to R=120mm,the angle 2φ=90∘.Find the magnetic induction of the field at the point O.
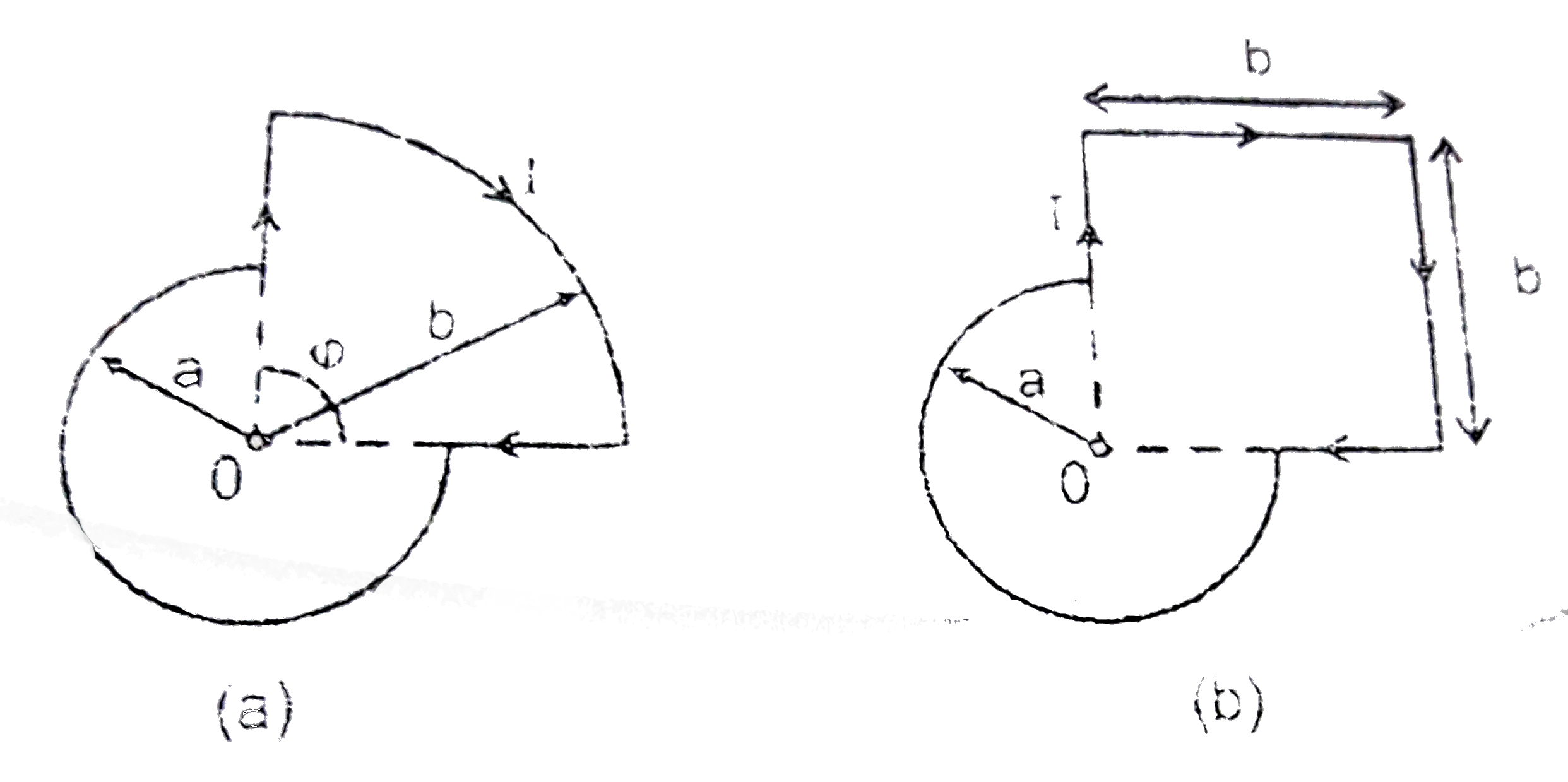
View SolutionThe current flowing through wire depends on time as, I=3t2+2t+5
The charge flowing through the cross - section of the wire in time t=0 to t=2 second is
View SolutionA thin wire is wound very tightly in one layer on the surface of a sphere of paramagnetic material (μr≈1). The planes of all the turns can be assumed to be perpendicular to the same diameter of the sphere. The turns over the entire surface of the sphere. The radius of the sphere is R, the total number of turns is N, and the current in the winding is I. Find the magnetic induction at the centre of the sphere. (Given μ0NI=20R)
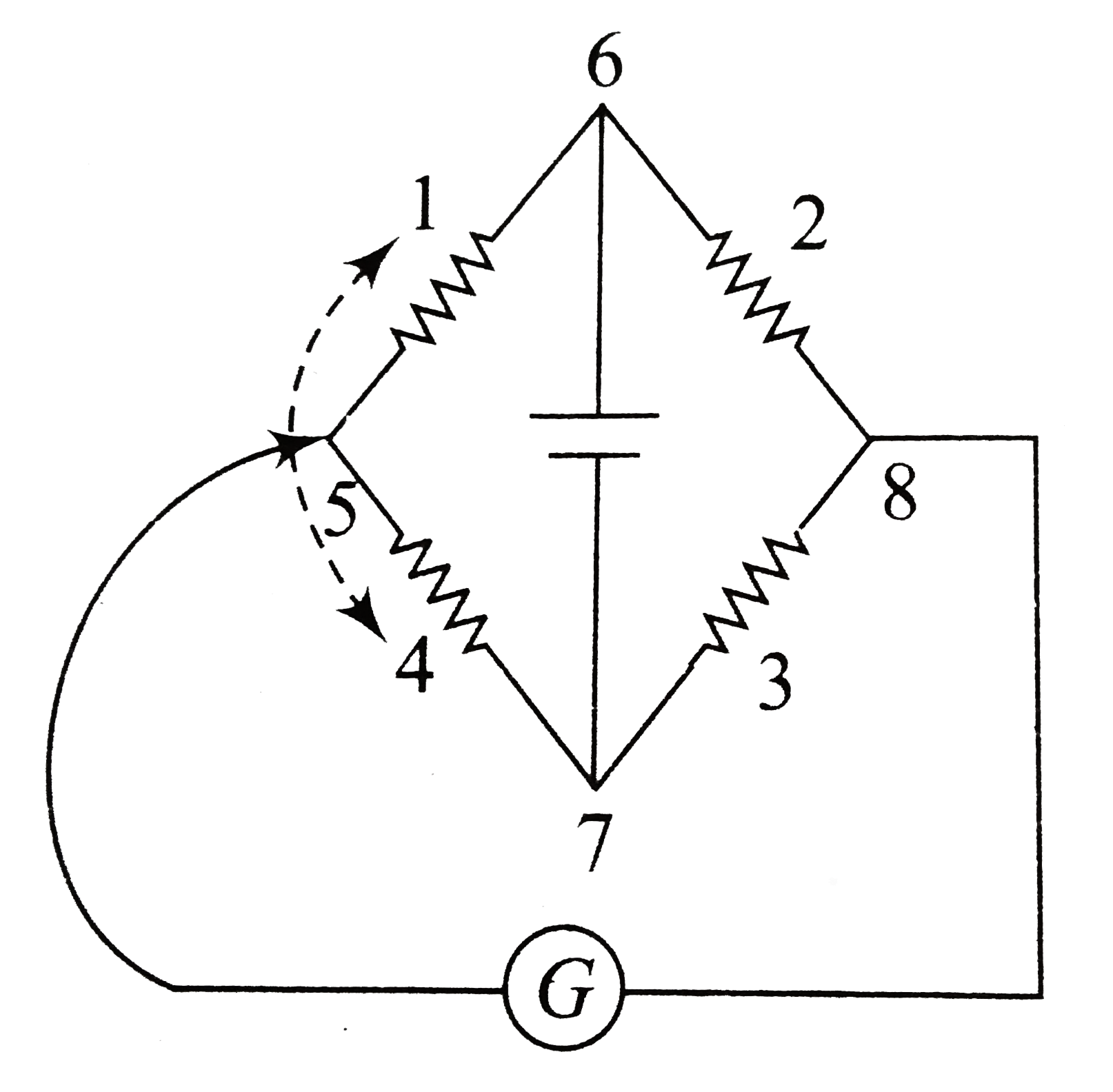
View SolutionFour wires of equal length 2 m are arranged as shown in the figure. Wires , 2, 3 and 4 are of equal cross-sectional area and wire 1 is of half the cross section of these wires. By how much distance pointer at point 5 must be moved to get null point ?
View SolutionA copper wire has a square cross-section, 2.0 mm on a side. It carries a current of 8 A and the density of free electrons is 8×1028m−3. The drift speed of electrons is equal to
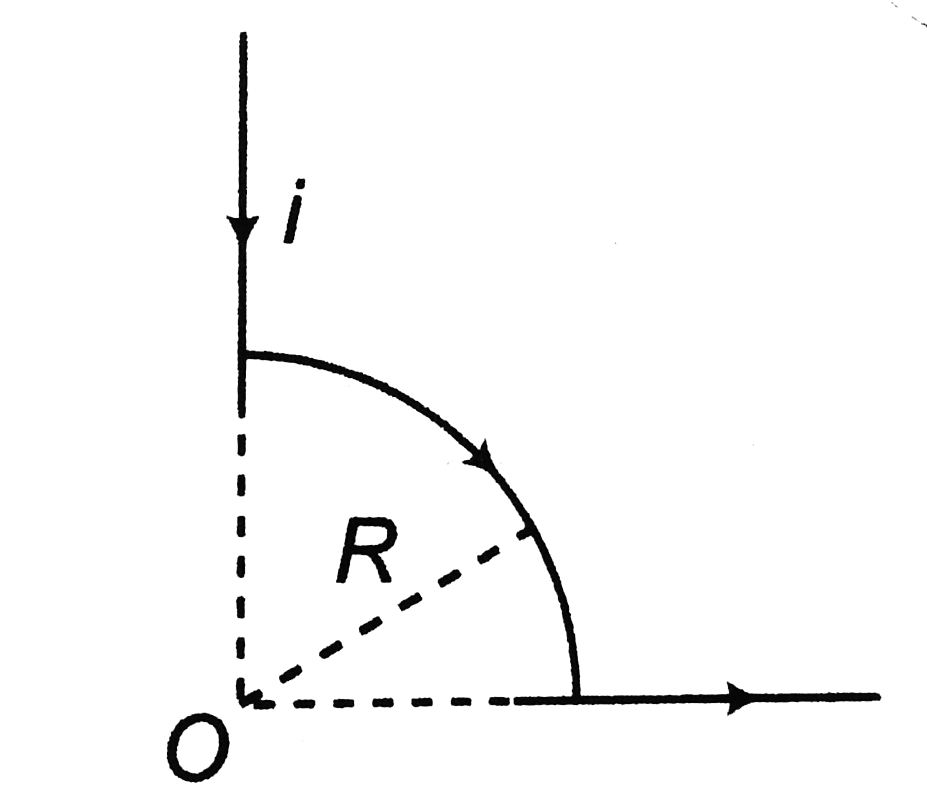
View SolutionThe segment of wire shown in figure carries a current of i=5.0A where the radius of the circular arc is R=3.0cm. Determine the magnitude and direction of the magnetic field at the origin.
View SolutionCalculate the electric current density in a uniform wire connected to a battery of emf 3.5 V and negligible internal resistance. The resistance of the wire is 2.0Ω and its area of cross-section is 0.70×10−6m2.
View Solution
