Choose the correct option:
Two identical conducting rods are first connected independently to two vessels, one containing water at 100∘C and the other containing ice at 0∘C. In the second case, the rods are joined end to end and connected to the same vessels. Let q1andq2 gram per second be the rate of melting of ice in the two cases respectively. The ratio q1q2 is:
(a) 12
(b)21
(c)41
(d)14
The correct Answer is:D
To solve the problem, we need to analyze the heat transfer through the two identical conducting rods in two different configurations: independent connections and a series connection.
1. Understanding the Setup:
- We have two identical conducting rods.
- In the first case, one rod is connected to water at 100∘C and the other to ice at 0∘C.
- In the second case, the rods are joined end to end (in series) and connected to the same vessels.
2. Heat Transfer and Melting of Ice:
- The rate of melting of ice, denoted as q, is proportional to the amount of heat transferred per second.
- According to Fourier's law of heat conduction, the rate of heat transfer Q through a conductor is given by:
Q=ΔTR
where ΔT is the temperature difference and R is the thermal resistance.
3. Thermal Resistance:
- For two identical rods, the thermal resistance R can be expressed as:
R=LkA
where L is the length of the rod, k is the thermal conductivity, and A is the cross-sectional area.
- Since the rods are identical, we can denote the resistance of one rod as R=r.
4. Case 1: Independent Connection:
- In this case, the rods are connected independently to the heat sources. The thermal resistance for each rod remains r.
- The effective resistance for the melting of ice (which is at 0∘C) is:
R1=r(for the rod connected to ice)
- The temperature difference for the rod connected to water is:
ΔT1=100∘C−0∘C=100∘C
- The rate of melting of ice in this case, q1, can be expressed as:
q1∝100r
5. Case 2: Series Connection:
- When the rods are joined end to end, the total resistance becomes:
R2=r+r=2r
- The temperature difference remains the same:
ΔT2=100∘C−0∘C=100∘C
- The rate of melting of ice in this case, q2, can be expressed as:
q2∝1002r=50r
6. Finding the Ratio:
- Now, we can find the ratio of the rates of melting of ice in the two cases:
q1q2=100r50r=10050=2
7. Final Ratio:
- Therefore, the ratio q1/q2 is:
q1q2=2or2:1
Conclusion:
The correct option is B: 2 by 1.
- We have two identical conducting rods.
- In the first case, one rod is connected to water at 100∘C and the other to ice at 0∘C.
- In the second case, the rods are joined end to end (in series) and connected to the same vessels.
- The rate of melting of ice, denoted as q, is proportional to the amount of heat transferred per second.
- According to Fourier's law of heat conduction, the rate of heat transfer Q through a conductor is given by:
Q=ΔTR
where ΔT is the temperature difference and R is the thermal resistance.
- For two identical rods, the thermal resistance R can be expressed as:
R=LkA
where L is the length of the rod, k is the thermal conductivity, and A is the cross-sectional area.
- Since the rods are identical, we can denote the resistance of one rod as R=r.
- In this case, the rods are connected independently to the heat sources. The thermal resistance for each rod remains r.
- The effective resistance for the melting of ice (which is at 0∘C) is:
R1=r(for the rod connected to ice)
- The temperature difference for the rod connected to water is:
ΔT1=100∘C−0∘C=100∘C
- The rate of melting of ice in this case, q1, can be expressed as:
q1∝100r
- When the rods are joined end to end, the total resistance becomes:
R2=r+r=2r
- The temperature difference remains the same:
ΔT2=100∘C−0∘C=100∘C
- The rate of melting of ice in this case, q2, can be expressed as:
q2∝1002r=50r
- Now, we can find the ratio of the rates of melting of ice in the two cases:
q1q2=100r50r=10050=2
- Therefore, the ratio q1/q2 is:
q1q2=2or2:1
The correct option is B: 2 by 1.
Topper's Solved these Questions
Similar Questions
Two identical conducting rods are first connected independently to two vessels, one containing water at 100∘C and the other containing ice at 0∘C. In the second case, the rods are joined end to end and connected to the same vessels. Let q1andq2 gram per second be the rate of melting of ice in the two cases respectively. The ratio q1q2 is
(a) 12 (b)21 (c)41 (d)14
View SolutionTwo identical conducting rods are first connected independently to two vessels, one containing water at 100∘C and the other containing ice at 0∘C. In the second case, the rods are joined end to end and connected to the same vessels. Let q1andq2 gram per second be the rate of melting of ice in the two cases respectively. The ratio q1q2 is
(a) 12 (b)21 (c)41 (d)14
View SolutionTwo identical conducting rods are first connected independently to two vessels, one containing water at 100∘C and the other containing ice at 0∘C. In the second case, the rods are joined end to end connected to the same vessels. Let m1andm2 g/s be the rate of melting of ice in the two cases respectively, the ratio m1m2 is
View SolutionSix identical conducting rods are connected as shown in figure. In steady state temperature of point ϕ1 is fixed at 100∘C and temperature of ϕ6 at −80∘C

Q. What is the temperature of ϕ2?
View SolutionSix identical conducting rods are connected as shown in figure. In steady state temperature of point ϕ1 is fixed at 100∘C and temperature of ϕ6 at −80∘C

Q. What is the temperature of ϕ3?
View SolutionSix identical conducting rods are connected as shown in figure. In steady state temperature of point ϕ1 is fixed at 100∘C and temperature of ϕ6 at −80∘C
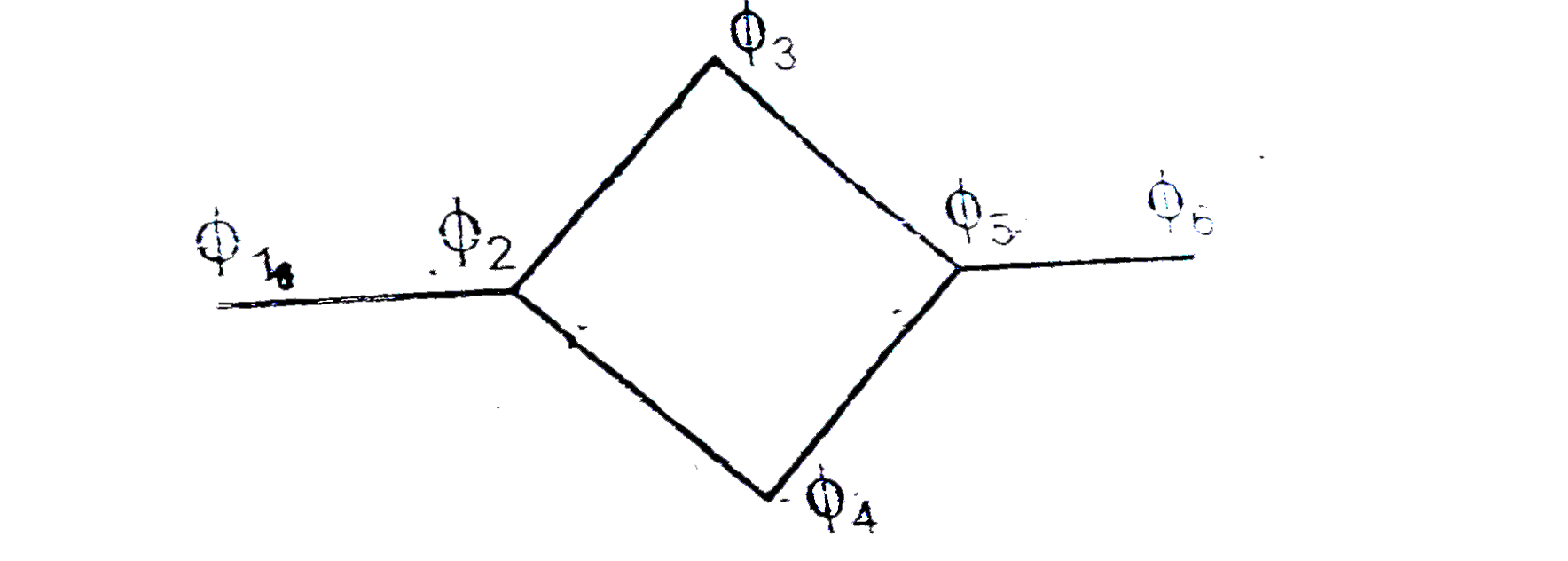
Q. What is the temperature of ϕ5?
View SolutionTwo identical rods are connected between two containers. One of them is at 100∘C containing water and another is at 0∘C containing ice. If rods are connected in parallel then the rate of melting of ice is q1g/s . If they are connected in series then teh rate is q2g/s . The ratio q2/q1 is
View SolutionTwo conducting rods when connected between two points at constant but different temperatures separately, the rate of heat flow through them is q1andq2.
View SolutionTwo chemically non-reactive gases are separately contained in two vessels of same capacity at pressure P1, and P2, respectively. If two vessels are connected, the total pressure of gaseous mixture will be
View SolutionTwo chemically non-reactive gases are separately contained in two vessels of same capacity at pressure P1 and P2 respectively. If two vessels are connected, the total pressure of gaseous mixture will
View Solution
