Question

Choose the correct option:

Water is filled in a cylindrical container to a height of ${\displaystyle 3m}$. The ratio of the cross-sectional area of the orifice and the beaker is ${\displaystyle 0.1}$. The square of the speed of the liquid coming out from the orifice is ${\displaystyle (g=10m/s^2)}$.

Options

A. (a) `50 m^(2)//s^(2)`
B. (b) `50.5m^(2)//s^(2)`
C. (c) `51m^(2)//s^(2)`
D. (d) `52 m^(2)//s^(2)`

Answer

A

Explanation

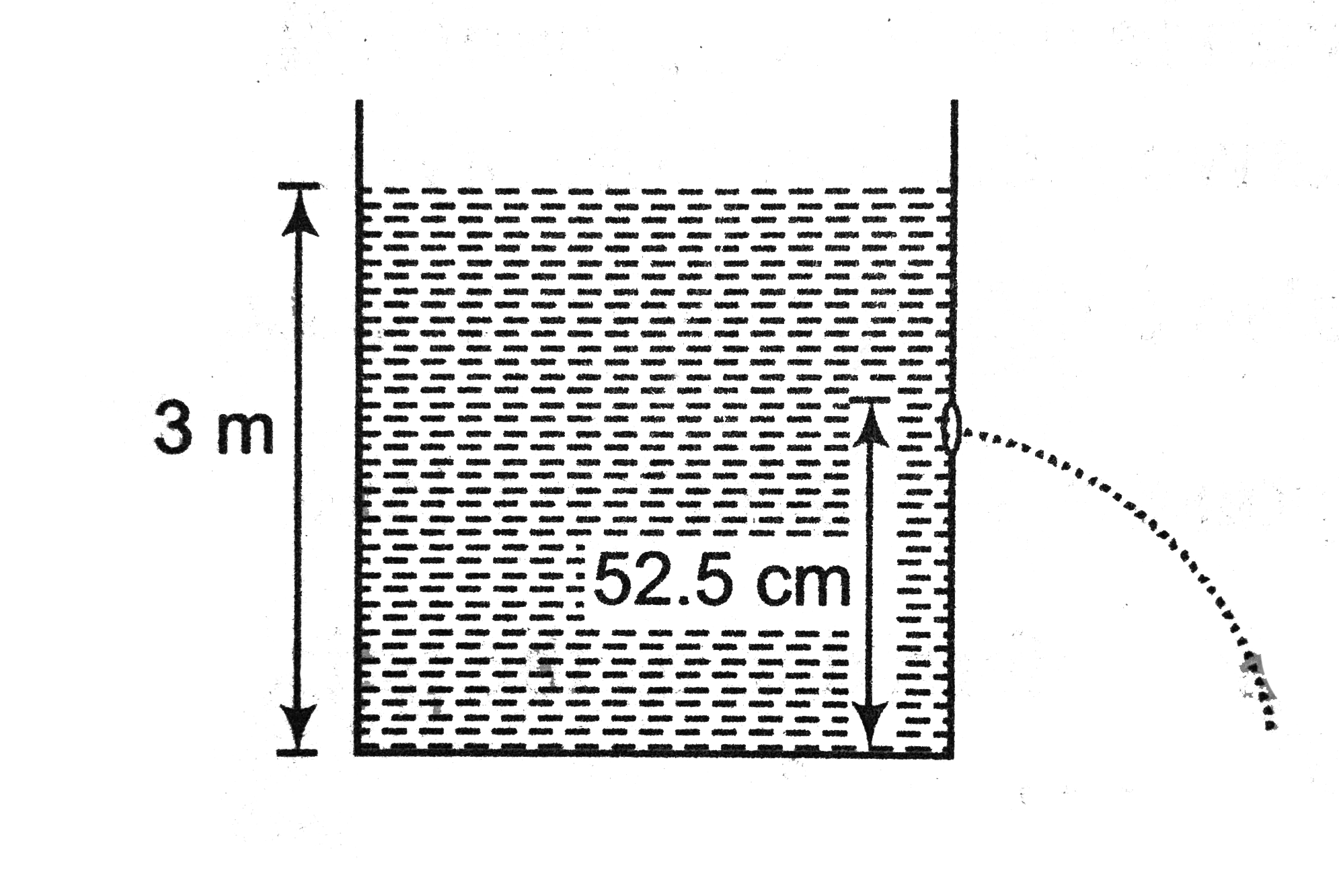
Applying continuity equation at 1 and 2, we have
`A_(1)v_(1)=A_(2)v_(2)`...(i)

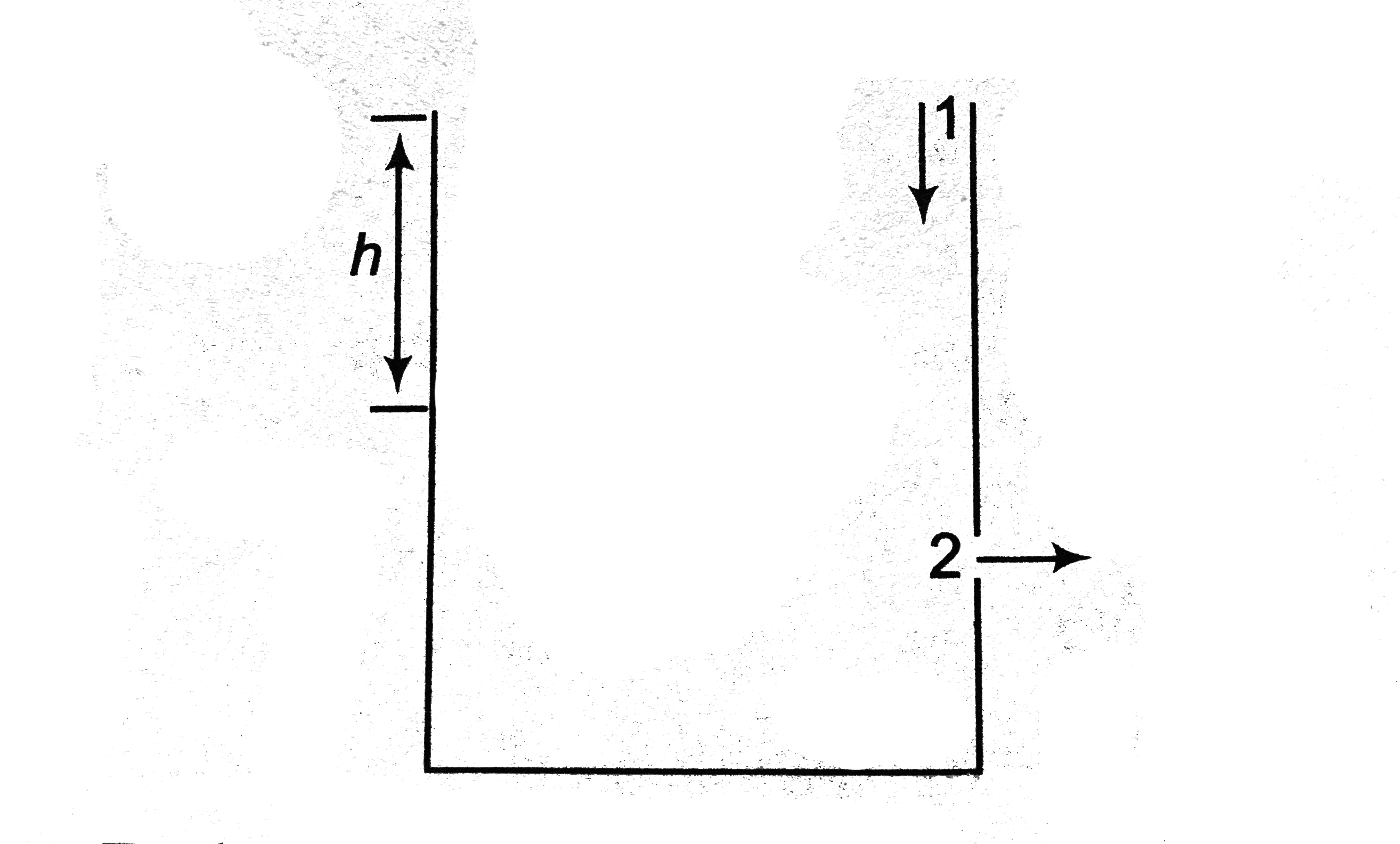
Further applying Bernoulli's equation at these two points, we have
`p_(0)+rho gh +(1)/(2) rho v_(1)^(2)=p_(0)+0+(1)/(2) rho v_(2)^(2)`...(ii)
Solving Eqs. (i) and (ii), we have `v_(2)^(2)=(2gh)/(I-(A_(2)^(2))/(A_(1)^(2)))`
Substituting the values, we have
`v_(2)^(2)=(2xx10xx2.475)/(1-(0.1)^(2))=50m^(2)//s^(2)`.