Condenser A has a capacity of 15μF when it is filled with a medium of dielectric constant 15. Another condenser B has a capacity 1μF with air between the plates. Both are charged separately by a battery of 100V. After charging, both are connected in parallel without the battery and the dielectric material being removed. The common potential now is
400 V
800 V
1200 V
1600 V
The correct Answer is:B
To solve the problem step by step, we will follow the reasoning laid out in the video transcript.
Step 1: Calculate the charge on each capacitor before they are connected.
1. Capacitor A has a capacitance CA=15μF and is charged to a potential V=100V.
- The charge QA on capacitor A can be calculated using the formula:
QA=CA×V=15μF×100V=1500μC
2. Capacitor B has a capacitance CB=1μF and is also charged to V=100V.
- The charge QB on capacitor B can be calculated as:
QB=CB×V=1μF×100V=100μC
Step 2: Calculate the total charge when both capacitors are connected in parallel.
- The total charge Qtotal when the two capacitors are connected in parallel is the sum of the charges on both capacitors:
Qtotal=QA+QB=1500μC+100μC=1600μC
Step 3: Determine the capacitance of capacitor A after the dielectric is removed.
- When the dielectric is removed, the capacitance of capacitor A changes. The capacitance with the dielectric is CA=15μF and the dielectric constant k=15. The capacitance without the dielectric is:
CA,air=CAk=15μF15=1μF
Step 4: Calculate the equivalent capacitance when both capacitors are connected in parallel.
- The capacitance of capacitor B remains the same since it was already in air:
CB=1μF
- The equivalent capacitance Ceq when both capacitors are connected in parallel is:
Ceq=CA,air+CB=1μF+1μF=2μF
Step 5: Calculate the common potential across the capacitors after they are connected.
- The common potential Vcommon across the capacitors can be found using the total charge and the equivalent capacitance:
Vcommon=QtotalCeq=1600μC2μF=800V
Final Answer:
The common potential when both capacitors are connected in parallel is 800V.
---
- The charge QA on capacitor A can be calculated using the formula:
QA=CA×V=15μF×100V=1500μC
- The charge QB on capacitor B can be calculated as:
QB=CB×V=1μF×100V=100μC
Qtotal=QA+QB=1500μC+100μC=1600μC
CA,air=CAk=15μF15=1μF
CB=1μF
Ceq=CA,air+CB=1μF+1μF=2μF
Vcommon=QtotalCeq=1600μC2μF=800V
The common potential when both capacitors are connected in parallel is 800V.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.5
20 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
Two condensers, one of capacity C and the other of capacity C/2 are connected to a V volt battery, as shown.
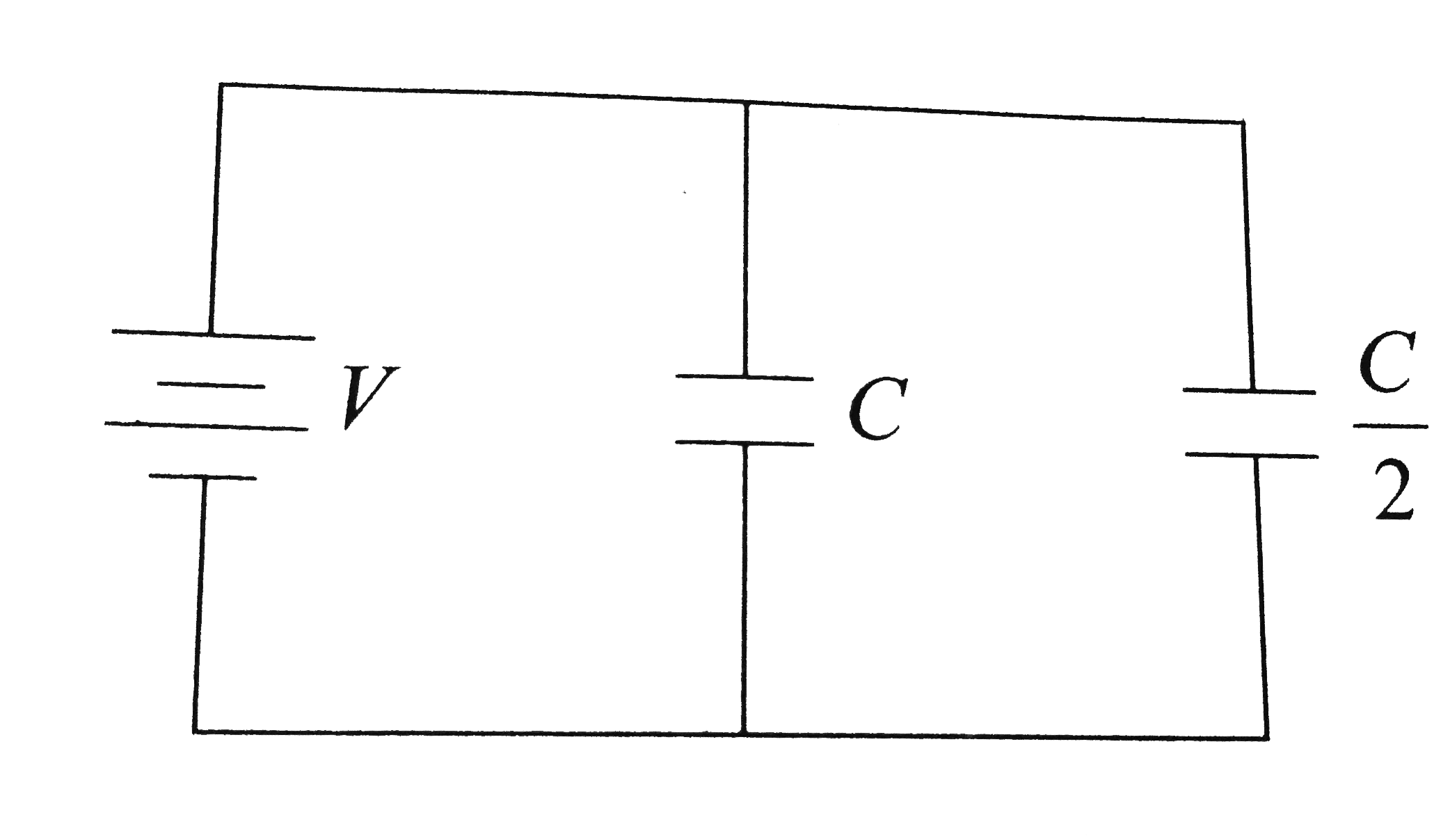
The work done in charging fully both the condensers is
View SolutionTwo condensers, one of capacity C and the other of capacity C/2 are connected to a V volt battery, as shown.

The work done in charging fully both the condensers is
View SolutionTwo condensers, one of capacity C and the other of capacity C/2 are connected to a V volt battery, as shown.

The work done in charging fully both the condensers is
View SolutionTwo condensers, one of capacity C and the other of capacity C/2 are connected to a V volt battery, as shown.

The work done in charging fully both the condensers is
View SolutionTwo condensers, one of capacity C and the other of capacity C/2 are connected to a V volt battery, as shown.

The work done in charging fully both the condensers is
View SolutionA parallel-plate capacitor having plate are 100cm2 and separation 1.0 mm holds a charge of 0.12μC when connected to a 120 V battery. Find the dielectric constant of the material filling the gap.
View SolutionA parallel plate capacitor with liquid filled between the plates (dielectric constant of liquid, k=4)has capacitance 20μF. If the liquid is removed then capacitance of capacitor becomes
View Solution0.2F capacitor is charged to 600V by a battery. On removing the battery it is connected with another parallel plate condenser of 1F. The potential decreases to
View SolutionA capacitor stores 50μc charge when connected across a battery . When the gap between the plates is filled with a dielectric , a charge of 100muc flows through the battery .Find the dielectric constant of the material inserted.
View SolutionA capacitor of capacitance 2μF has a dielectric slab of dielectric constant 8 between its plates. The slab covers the entire volume between the plates. This capacitor is connected to a battery if EMF 20 V and fully charged Now with the battery still connected, the slab is removed from the capactor. during the removal, the work done by the battery is (in mJ).
View Solution
