Conider a given sample of an ideal gas (CpCv=γ) having initial pressure (p0)andvolume(V0) . (a) The gas is isothermally taken to a pressure (P02) and from there adiabatically ta a pressure (p02) and from there isothermally to a pressure (p04) . find the volume.
To solve the problem step-by-step, we will analyze the process of the ideal gas as it undergoes different transformations: isothermal and adiabatic.
Step 1: Initial Conditions
We start with an ideal gas at initial pressure P0 and volume V0.
Step 2: Isothermal Process to Pressure P02
In an isothermal process, the product of pressure and volume remains constant. Therefore, we have:
P0V0=P′V′
where P′=P02 is the pressure after the isothermal process, and V′ is the new volume.
Substituting the values, we get:
P0V0=P02V′
Now, we can solve for V′:
V′=P0V0P02=2V0
Step 3: Adiabatic Process to Pressure P04
In an adiabatic process, the relationship between pressure and volume is given by:
PVγ=constant
Let’s denote the pressure after the isothermal process as P′=P02 and the volume as V′=2V0. The final pressure after the adiabatic process is Pf=P04.
Using the adiabatic condition:
P′(V′)γ=Pf(Vf)γ
Substituting the known values:
(P02)(2V0)γ=(P04)(Vf)γ
Step 4: Simplifying the Equation
Now, we simplify the equation:
P02⋅2γVγ0=P04Vγf
Cancelling P0 from both sides:
12⋅2γVγ0=14Vγf
Multiplying both sides by 4:
2⋅2γVγ0=Vγf
Step 5: Solving for Vf
Now we can express Vf:
Vγf=2γ+1Vγ0
Taking the γ-th root of both sides gives:
Vf=2γ+1γV0
This can also be written as:
Vf=21+1γV0
Final Answer
Thus, the final volume Vf after the entire process is:
Vf=21+1γV0
---
We start with an ideal gas at initial pressure P0 and volume V0.
In an isothermal process, the product of pressure and volume remains constant. Therefore, we have:
In an adiabatic process, the relationship between pressure and volume is given by:
Now, we simplify the equation:
Now we can express Vf:
Thus, the final volume Vf after the entire process is:
Topper's Solved these Questions
Similar Questions
An ideal gas (Cp/Cv=γ) having initial pressure P0 and volume V0 (a) The gas is taken isothermally to a pressure 2P0 and then adiabatically to a pressure 4P0. Find the final volume. (b) The gas is brought back to its initial state. It is adiabatically taken to a pressure 2P0 and then isothermally to a pressure 4P0. Find the final volume.
View SolutionThe pressure p and volume V of an ideal gas both increase in a process.
View SolutionThe pressure P and volume V of an ideal gas both decreases in a process.
View SolutionA monatomic gas at a pressure P, having a volume V expands isothermally to a volume 2 V and then adiabatically to a volume 16 V. The final pressure of the gas is ( take γ=53)
View SolutionThe initial pressure and volume of a given mass of a gas (CpCv=γ) are (p0) and (V0). The gas can exchange heat with surrounding. (a) It is slowly compressed to a volume (V02) and then suddenly compressed to (V04) . Find the final pressure. (b) If the gas is suddenly cpmpressed from the volume (V0→V02) and then slowly compressed to (V04), What will be the final pressure?.
View SolutionA sample of an ideal gas with initial pressure 'P' and volume 'V' is taken through an isothermal process during which entropy change is found to be DS. The work done by the gas is
View SolutionAn ideal gas undergoes a process P→Q→R as shown in pressure (p) - volume (v) diagram.The work done by the gas is
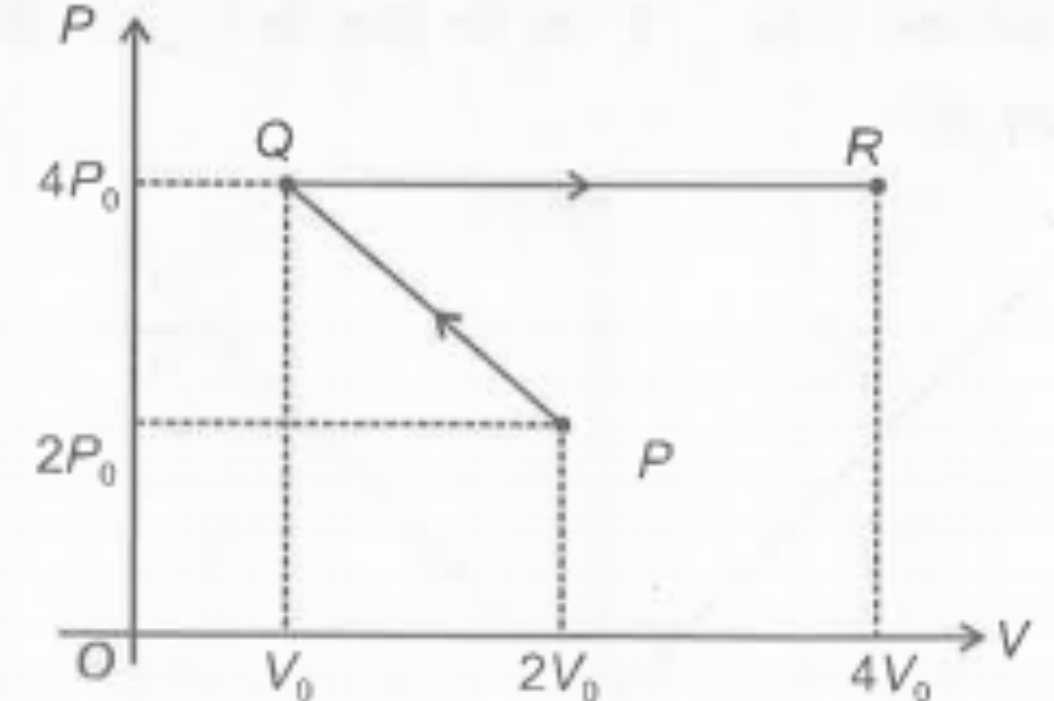
View SolutionWhen an ideal gas at pressure P, temperature T and volume V is isothermally compressed to V/n. its pressure becomes Pi. If the gas is compressed adiabatically to V/n, its pressure becomes Pa. The ratio Pi/Pa is: ( l=CP/CV)
View SolutionIf a gas of a volume V1 at pressure p1 is compressed adiabatically to volume V2 and pressure p2, calculate the work done by the gas.
View SolutionAn ideal gas of volume V and pressure P expands isothermally to volume 16 V and then compressed adiabatically to volume V . The final pressure of gas is [γ=1.5]
View Solution
