A sample of an ideal gas with initial pressure 'P' and volume 'V' is taken through an isothermal process during which entropy change is found to be DS. The work done by the gas is
PVΔSnR
nRΔS
PV
PΔSnRV
To find the work done by an ideal gas during an isothermal process when the entropy change is given as ΔS, we can follow these steps:
Step 1: Understand the Isothermal Process
In an isothermal process, the temperature (T) of the gas remains constant. For an ideal gas, the relationship between pressure (P), volume (V), and temperature (T) is given by the ideal gas law:
PV=nRT
where n is the number of moles and R is the universal gas constant.
Step 2: Relate Entropy Change to Work Done
The change in entropy (ΔS) for an ideal gas during an isothermal process can be expressed as:
ΔS=QT
where Q is the heat exchanged. For an isothermal process, the work done (W) by the gas is equal to the heat absorbed by the gas:
W=Q
Step 3: Substitute for Q
From the equation for entropy change, we can rearrange it to find Q:
Q=TΔS
Step 4: Relate Work Done to Entropy Change
Since the work done by the gas in an isothermal process is equal to the heat absorbed, we can substitute Q into the equation for work:
W=TΔS
Step 5: Substitute for T Using Ideal Gas Law
From the ideal gas law, we can express T as:
T=PVnR
Now, substitute this expression for T into the work equation:
W=(PVnR)ΔS
Step 6: Final Expression for Work Done
Thus, the work done by the gas can be expressed as:
W=PVΔSnR
Conclusion
The work done by the gas during the isothermal process is:
W=PVΔSnR
In an isothermal process, the temperature (T) of the gas remains constant. For an ideal gas, the relationship between pressure (P), volume (V), and temperature (T) is given by the ideal gas law:
PV=nRT
where n is the number of moles and R is the universal gas constant.
The change in entropy (ΔS) for an ideal gas during an isothermal process can be expressed as:
ΔS=QT
where Q is the heat exchanged. For an isothermal process, the work done (W) by the gas is equal to the heat absorbed by the gas:
W=Q
From the equation for entropy change, we can rearrange it to find Q:
Q=TΔS
Since the work done by the gas in an isothermal process is equal to the heat absorbed, we can substitute Q into the equation for work:
W=TΔS
From the ideal gas law, we can express T as:
T=PVnR
Now, substitute this expression for T into the work equation:
W=(PVnR)ΔS
Thus, the work done by the gas can be expressed as:
W=PVΔSnR
The work done by the gas during the isothermal process is:
W=PVΔSnR
Similar Questions
The pressure P and volume V of an ideal gas both decreases in a process.
View SolutionOne mole of an ideal diatomic gas is taken through a process whose P−V diagram is shown in the figure. The work done by the gas is
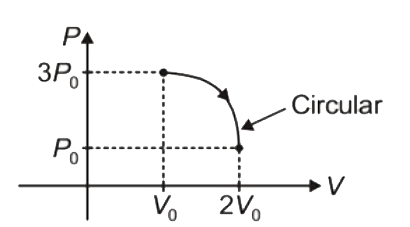
View SolutionThe pressure p and volume V of an ideal gas both increase in a process.
View SolutionThe change in internal energy of two moles of a gas during adiabatic expansion is found to be -100 Joule. The work done during the process is
View SolutionChange in internal energy in an isothermal process for ideal gas is
View SolutionConider a given sample of an ideal gas (CpCv=γ) having initial pressure (p0)andvolume(V0) . (a) The gas is isothermally taken to a pressure (P02) and from there adiabatically ta a pressure (p02) and from there isothermally to a pressure (p04) . find the volume.
View SolutionThe state of an ideal gas is changed through an isothermal process at temperature T0 as shown in figure. The work done by the gas in going from state B to C is double the work done by gas in going from state A to B. If the pressure in the state B is p02, then the pressure of the gas in state C is
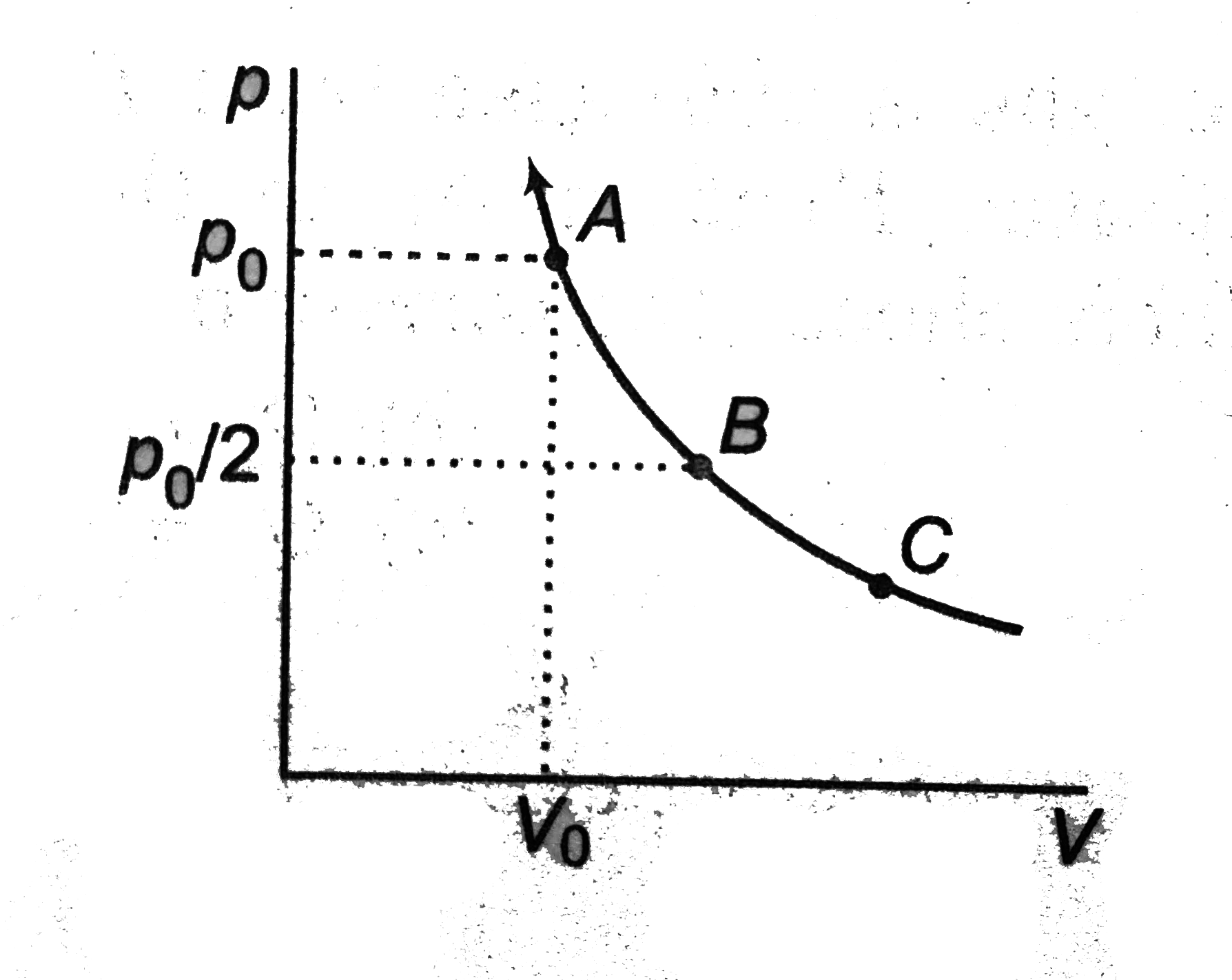
View SolutionThe state of an ideal gas is changed through an isothermal process at temperature T0 as shown in figure. The work done by the gas in going from state B to C is double the work done by gas in going from state A to B. If the pressure in the state B is p02, then the pressure of the gas in state C is

View SolutionIn a process, the pressure of an ideal gas is proportional to square of the volume of the gas. If the temperature of the gas increases in this process, then work done by this gas
View SolutionPi,Viare initial pressure and volumes and Vf is final volume of a gas in a thermodynamic process respectively. If PVn= constant, then the amount of work done by gas is:(γ=Cp/Cv). Assume same, initial states & same final volume in all processes.
View Solution