Consider a gravity free hall in which a tray of mas M, carrying a cubical block of icce of mas m and edge L, is at rest in the middle.. If the ice melts, by what distnce does the centre of mass of the tray plus the ice system descend?
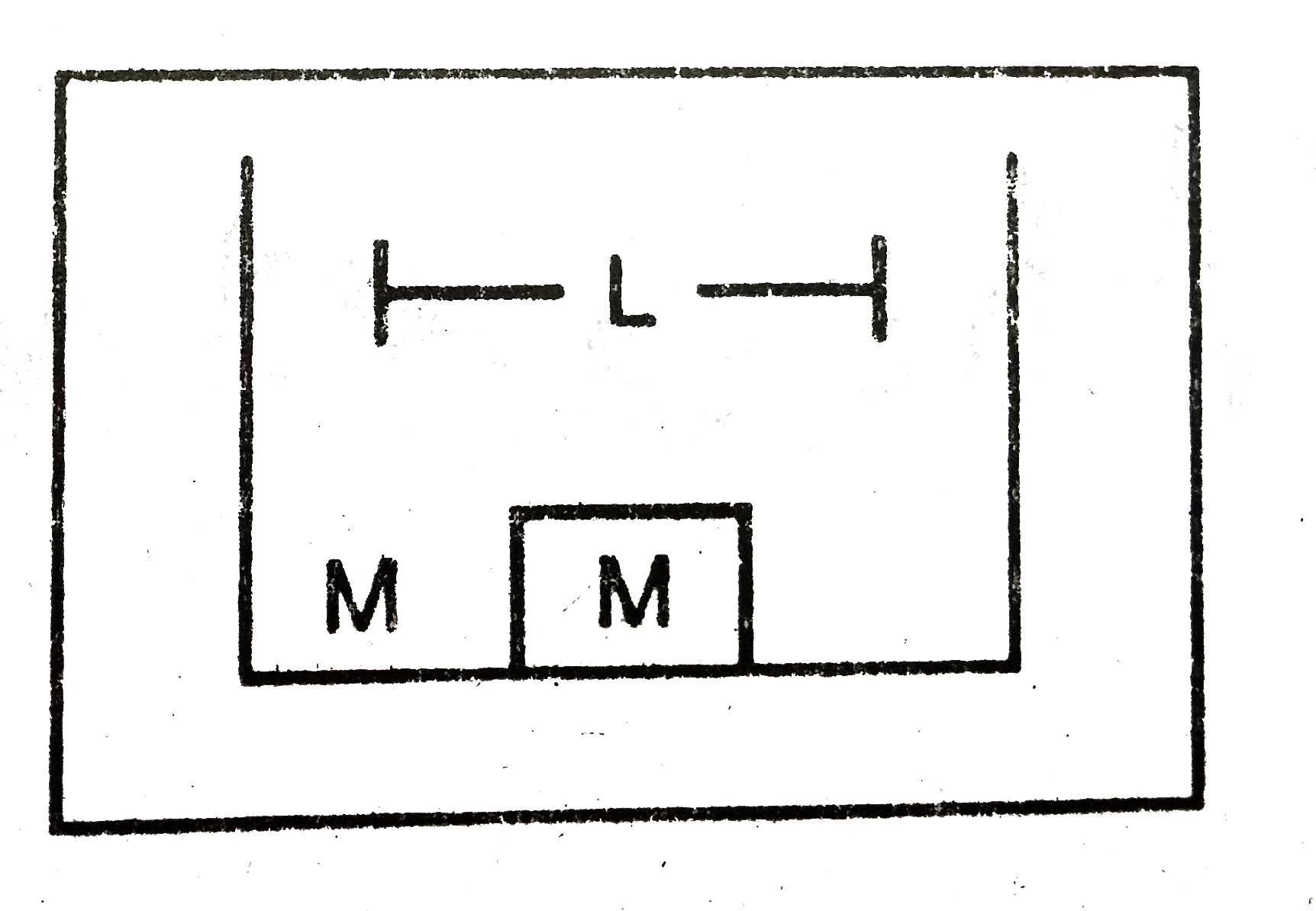
As there is gravity free after the ice melts, It would tend toacquire a phereicla shape. But, there is no exterN/Al force acting on the system. So, the centre of mass of the system
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMACHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective 2
11 Videos
- CALORIMETRYBOOK - HC VERMACHAPTER - CALORIMETRYEXERCISE - Exercises
18 Videos
- CIRCULAR MOTIONBOOK - HC VERMACHAPTER - CIRCULAR MOTIONEXERCISE - Exercises
30 Videos
Similar Questions
A cubical block of ice of mass m and edge L is placed in a large tray of mass M. If the ice melts, how far does the centre of mass of the system ''ice plus tray'' come down?
View SolutionThe ballon the light rope and the monkey shown in figure are at rest in the air. If the monkey reaches the top of the rope, by what distnce does the ballon descend? Mass of the ballon =M mass of the monkey =m and the length of the rope ascended by the monkey =L
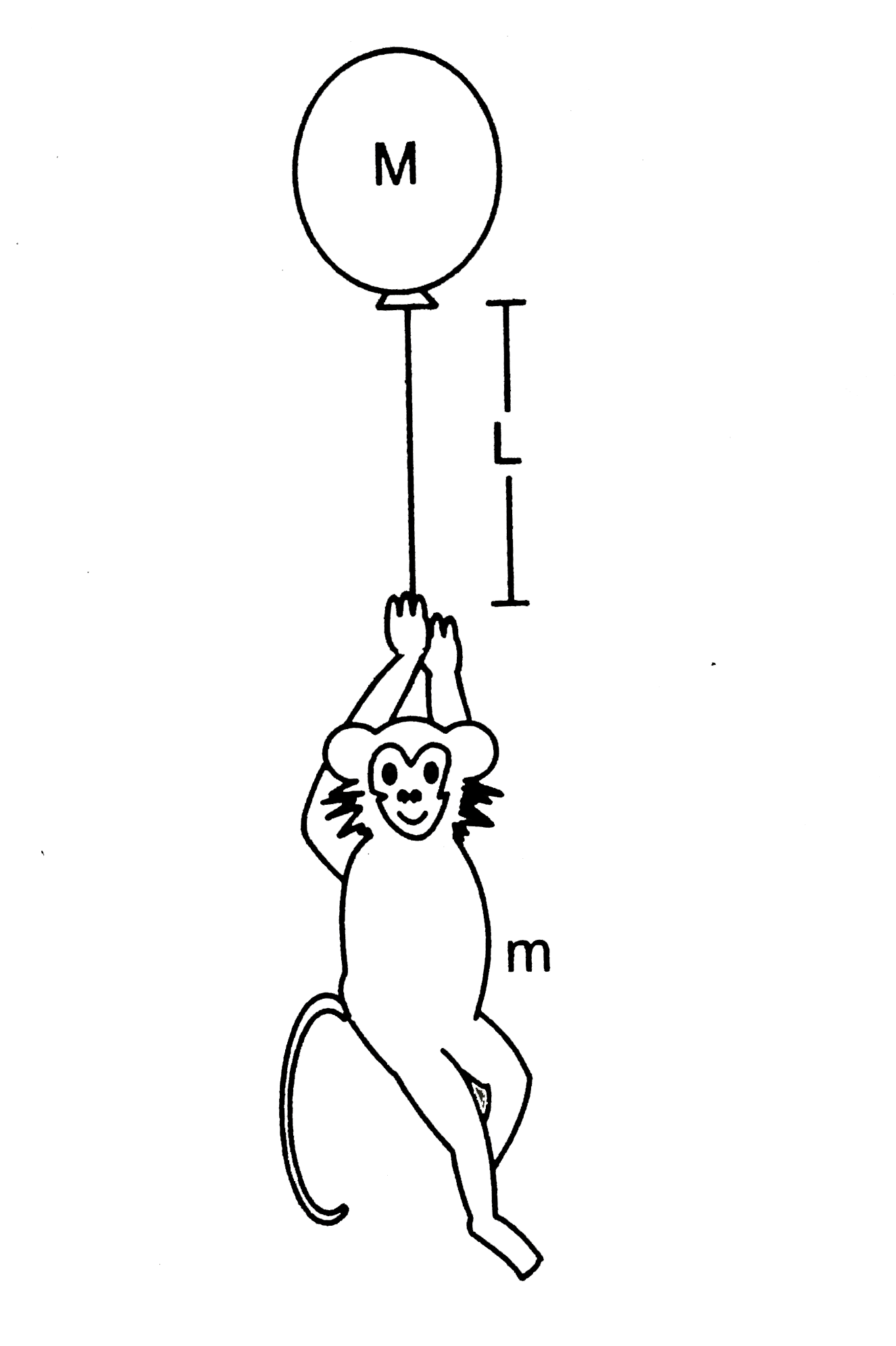
View Solution
Knowledge Check
A man of mass m stands at the left end of a uniform plank of length L and mass M, which lies on a frictionaless surface of ice. If the man walks to the other end of the plank, then by what distance does the plank slide on the ice?
ALBMLm+MCmLMDmLm+MAccording to the principle of conservation of linear momentum if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
A plank of mass M is placed on a smooth horizontal surface. light identical springs, each of stiffness K, are rigidly connected to struts at the end of the plank as shown in Fig. When the springs are in their unextended position, the distance between their free ends is 3l. A block of mass m is placed on the plank and pressed against one of the springs so that it is compressed to l. To keep the block at rest it is connected to the strut means of a light string. Initially, the system is at rest, Now the string is burnt.
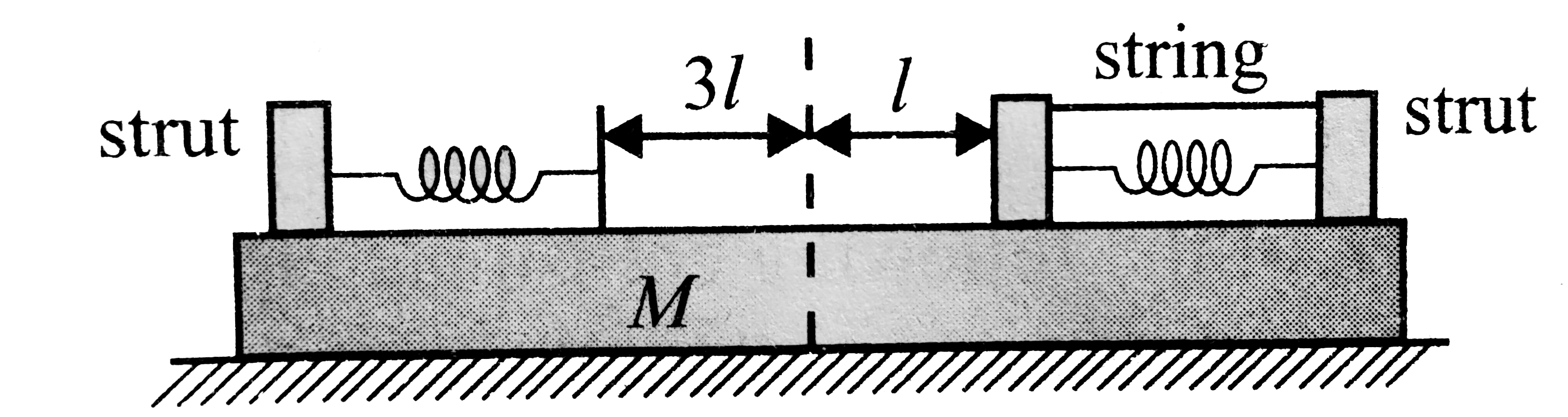
The maximum kinetic energy of the block m isAKml22M(M+m)BKml2M(M+m)CKMl22(M+m)Dnone of theseAccording to the principle of conservation of linear momentum if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
A plank of mass M is placed on a smooth horizontal surface. light identical springs, each of stiffness K, are rigidly connected to struts at the end of the plank as shown in Fig. When the springs are in their unextended position, the distance between their free ends is 3l. A block of mass m is placed on the plank and pressed against one of the springs so that it is compressed to l. To keep the block at rest it is connected to the strut means of a light string. Initially, the system is at rest, Now the string is burnt.

The maximum velocity of the plank isA√Km(M+m)lB√k(M+m)lC√KmM(M+m)lD√kMm(M+m)l
Two beads each of mass m are fixed on a light rigid rod of length 2l which is free to rotate in a horizontal plane. The bead on the far end is given some velocity υ as shown in the figure. If Kcm represents the kinetic energy of the centre of mass of the system and KR represents the rotational kinetic energy of the system, then what is the value of KcmKR?
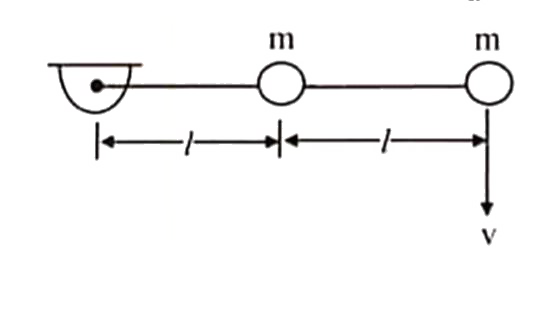
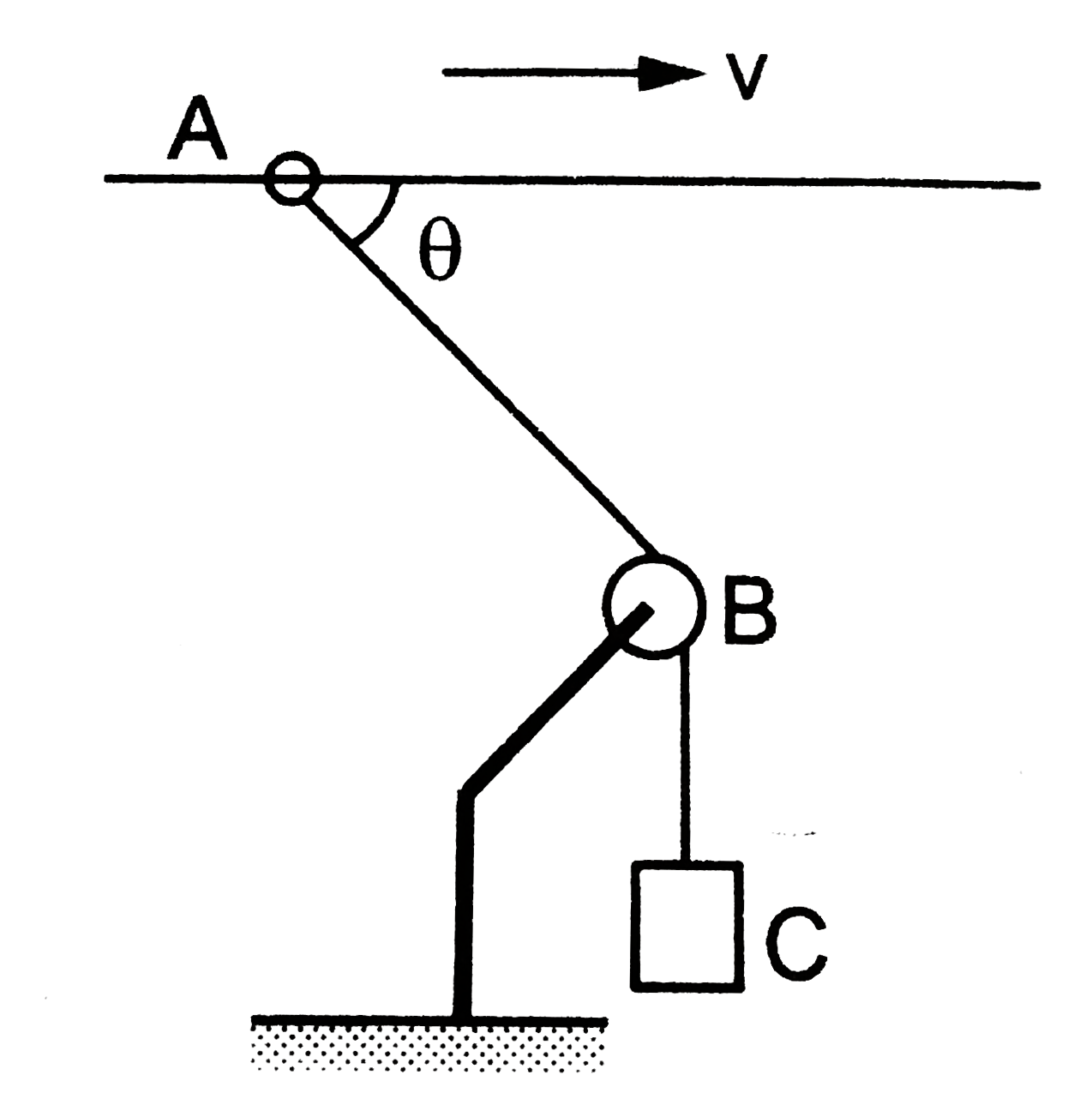
View SolutionA smooth ring A of mass m can slide on a fixed horizontal rod. A string tied to the ring passes over a fixed pulley B and carries a block C of ma M(=2m) as shown in figure. At an instant the string between the ring and the pulley makes an angle θ with the rod. a. Show that, if the ring slides with a pspeed v, the blockdescends with speed vcosθ, b. With whast acceleration will the ring starts moving if the system is released from rest with θ=300
View SolutionA wheel of moment of inertia I and rdius r is free to rotate about its centre as shown in figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. Find the speed of the block as it descends through a height h.

View SolutionA plank of mas M and length L is at rest on as frictionless floor. The top surface of the plank has friction. At one end of it a man of mass m is standing as shown in figure. If the man walks towards the other end the find the distance, which the plank moves a till the man reaches the centre of the plank. b. till the man reaches the other end of the plank.

View SolutionAccording to the principle of conservation of linear momentum if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
A plank of mass M is placed on a smooth horizontal surface. light identical springs, each of stiffness K, are rigidly connected to struts at the end of the plank as shown in Fig. When the springs are in their unextended position, the distance between their free ends is 3l. A block of mass m is placed on the plank and pressed against one of the springs so that it is compressed to l. To keep the block at rest it is connected to the strut means of a light string. Initially, the system is at rest, Now the string is burnt.
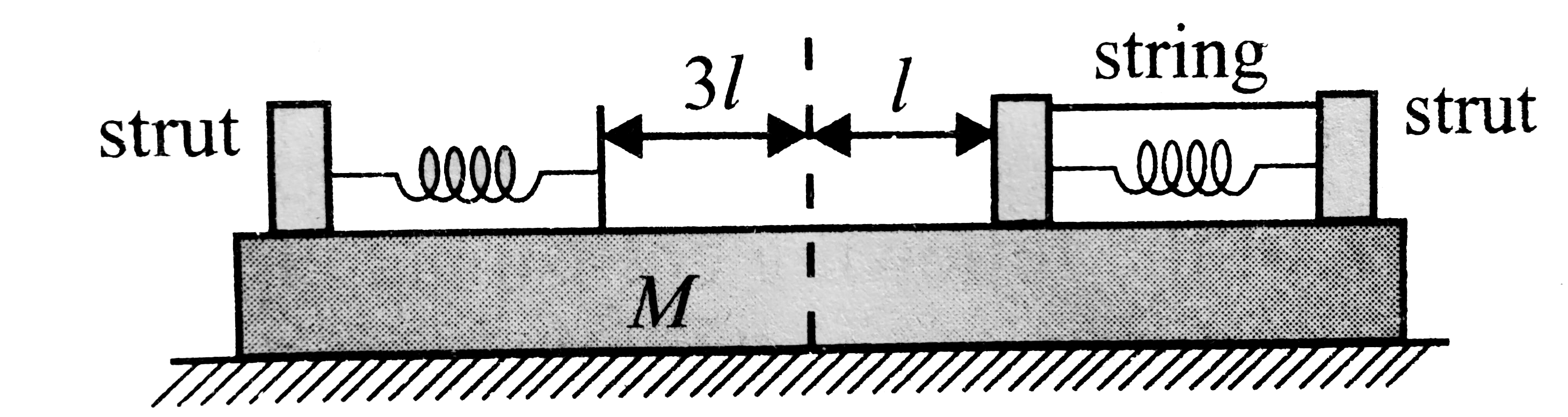
The maximum displacement of the plank is
View Solution
