Consider a thin uniform spherical layer of mass M and radius R. The potential energy of gravitational interaction of matter forming this shell is :
−GM2R
−GM22R
−35GM2R
−GM24R
The correct Answer is:B
To find the potential energy of gravitational interaction of a thin uniform spherical layer of mass M and radius R, we can follow these steps:
1. Understanding the Problem:
We have a thin uniform spherical shell of mass M and radius R. We need to calculate the gravitational potential energy associated with this shell.
2. Gravitational Potential Energy Formula:
The gravitational potential energy V between two masses m1 and m2 separated by a distance r is given by:
V=−Gm1m2r
where G is the gravitational constant.
3. Consider a Small Mass Element:
To calculate the total potential energy of the shell, we can consider a small mass element dm located on the shell. The potential energy due to the interaction of this mass element with the entire shell can be considered.
4. Integrating Over the Shell:
The total potential energy U of the shell can be calculated by integrating the potential energy contributions from all mass elements dm in the shell:
U=∫Vdm=∫−GMdmR
Here, R is the radius of the shell, and M is the total mass of the shell.
5. Setting Up the Integral:
Since the shell has a uniform mass distribution, we can express dm in terms of the total mass M:
dm=M4πR2dA
where dA is the differential area element on the surface of the sphere.
6. Calculating the Integral:
The total area of the shell is 4πR2, and thus:
U=−GMR∫dm=−GMR⋅M=−GM2R
7. Final Result:
The potential energy of gravitational interaction of the matter forming the shell is:
U=−GM22R
Conclusion:
The potential energy of gravitational interaction of the thin uniform spherical layer of mass M and radius R is given by:
U=−GM22R
We have a thin uniform spherical shell of mass M and radius R. We need to calculate the gravitational potential energy associated with this shell.
The gravitational potential energy V between two masses m1 and m2 separated by a distance r is given by:
V=−Gm1m2r
where G is the gravitational constant.
To calculate the total potential energy of the shell, we can consider a small mass element dm located on the shell. The potential energy due to the interaction of this mass element with the entire shell can be considered.
The total potential energy U of the shell can be calculated by integrating the potential energy contributions from all mass elements dm in the shell:
U=∫Vdm=∫−GMdmR
Here, R is the radius of the shell, and M is the total mass of the shell.
Since the shell has a uniform mass distribution, we can express dm in terms of the total mass M:
dm=M4πR2dA
where dA is the differential area element on the surface of the sphere.
The total area of the shell is 4πR2, and thus:
U=−GMR∫dm=−GMR⋅M=−GM2R
The potential energy of gravitational interaction of the matter forming the shell is:
U=−GM22R
The potential energy of gravitational interaction of the thin uniform spherical layer of mass M and radius R is given by:
U=−GM22R
Topper's Solved these Questions
Similar Questions
A uniform metal sphere of radius R and mass m is surrounded by a thin uniform spherical shell of same mass and radius 4R. The centre of the shell C falls on the surface of the inner sphere. Find the gravitational fields at points A and B.

View SolutionFor a given uniform spherical shell of mass M and radius R find gravitational field at a distancer r from centre in following two cases (a) r≥R (b) r<R .
View Solution
Knowledge Check
A particle of mass m is placed at the centre of a unifrom spherical shell of mass 3 m and radius R The gravitational potential on the surface of the shell is .
AGMRB−GMRC−4GMRD−2GMRA particle of mass M is placed at the centre of a spherical shell of same mass and radius a. What will be the magnitude of the gravitational potential at a point situated at a/2 distance from the centre ?
A−3GMRB−2GMRC−GMRD−4GMR
A uniform metal sphere of radius a and mass M is surrounded by a thin uniform spherical shell of equal mass and redius 4a. The centre of the shell falls on the surface of the iner sphere
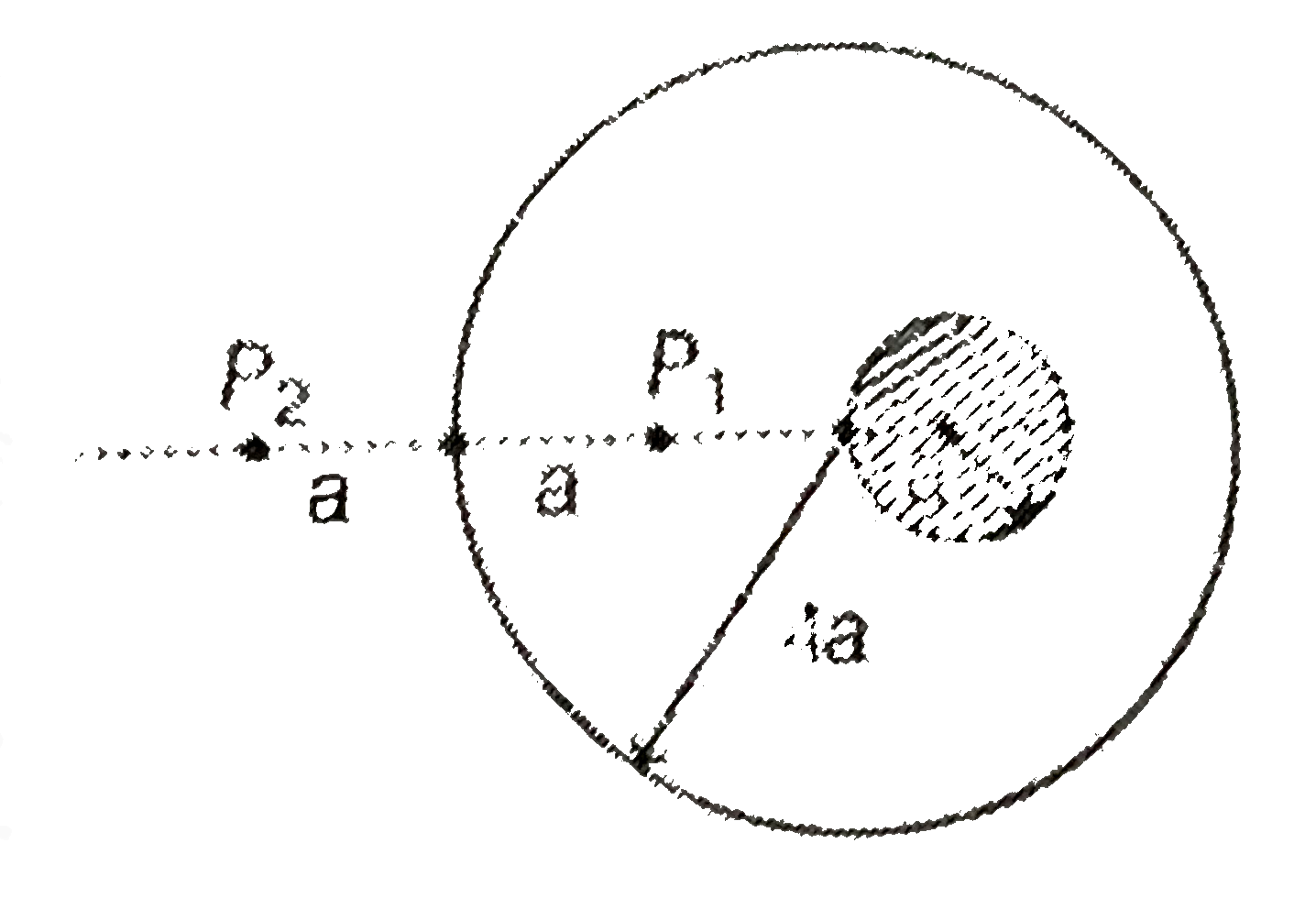
View SolutionA small area is removed from a uniform spherical shell of mass M and radius R. Then the gravitatioinal field intensity near the hollow portion is
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the centre.
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the centre.
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the center.
View SolutionConsider a ring of mass m and radius r. Maximum gravitational intensity on the axis of the ring has value.
View Solution
